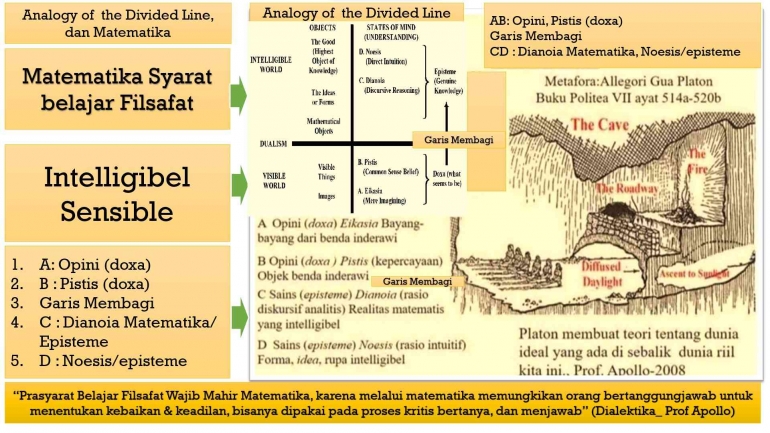
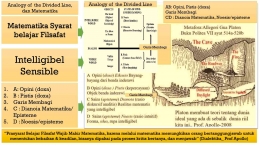
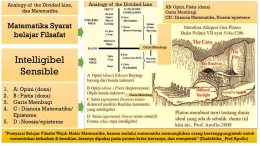
Fakta garis lurus antara dua titik adalah yang terpendek adalah proposisi sintetik. Karena konsep saya tentang garis lurus tidak memuat apa pun tentang ukuran, tetapi hanya kualitas. Oleh karena itu, konsep terpendek ditambahkan sepenuhnya dan tidak dapat dihilangkan dari konsep melalui pembedahan apa pun Garis lurus dapat ditarik. Oleh karena itu, intuisi harus digunakan di sini. (Kant, Kritik Akal Budi Murni)

Di sini, sifat kualitatif seluruh ruang Euclidean diakui secara matematis, yaitu kedatarannya, yang membuatnya berbeda secara kualitatif dari ruang lain seperti bola atau alam semesta yang melengkung. Artinya matematika tidak lagi sekedar teori besaran, tetapi mengkaji sifat-sifat kualitatif. Namun, hal ini tidak berarti ia terlepas dari filsafat dan sejarah. Lebih jauh lagi, harus ditentukan secara filosofis tempat apa yang ditempati matematika dalam pengetahuan tentang alam dan atas landasan apa matematika itu didasarkan.
Hegel tentang matematika alamAksioma tak terhingga dalam kalkulus diferensial. Bagi Hegel, pencapaian luar biasa dari filsafat terletak pada perancangan metodenya. Dengan itu ia dapat mengorientasikan dirinya ke mana saja dan menyelesaikan masalah apa pun. Hubungan antara matematika dan filsafat menjadi perbandingan metode: di sini aksiomatik, di sana dialektis. Geometri Euclidean menjadi contoh cemerlang keberhasilan metode aksiomatik, dan Hegel dengan tepat mengakuinya dalam semua ilmu alam yang meniru geometri Euclidean, seperti mekanika klasik.
Namun dalam ilmu logika matematika tidak digabungkan dengan geometri. Hegel memberikan status khusus pada kalkulus diferensial. Meskipun aksioma Euclid telah berlaku selama lebih dari 2000 tahun, sistem aksioma untuk kalkulus diferensial belum ditetapkan secara sistematis hingga zaman Hegel dan baru pada abad ke-20.
(a) Pengukuran dan intuisi geometri. Kalkulus diferensial didahului dengan penyelidikan geometri yang kembali ke pertanyaan tentang mengkuadratkan lingkaran. Kurva lengkung secara sistematis didekati dengan garis singgung lurus dengan tujuan untuk menyatakan lingkaran melalui sistem garis singgung, melalui poligon. Untuk fungsi sederhana seperti y = x, turunannya dapat ditebak menggunakan metode geometri dengan mengukur di banyak titik sehingga kemiringan garis singgung di titik x bernilai 2x.
Transformasi simbolisme tersebut mengatakan aturan perhitungan aritmatika ditinggalkan dan berlaku aturan baru. Lagrange mengadopsi simbolisme ini. Leibniz merumuskan kalkulus diferensial, yang mendefinisikan bagaimana simbol-simbol ini dapat dihitung tanpa terjadi kontradiksi ketika membaginya dengan nol.
Namun ketika Cauchy menerapkan kalkulus diferensial pada himpunan bilangan lain (bilangan kompleks), menjadi jelas validitas kalkulus diferensial merupakan properti himpunan bilangan yang derivasinya berlangsung dan karena itu termasuk dalam aksiomatik dari kumpulan angka ini. Misalnya pada himpunan bilangan asli tidak dapat diturunkan karena proses limit tidak mungkin dilakukan jika jarak antara dua bilangan asli yang berdekatan selalu satu. Dalam perkembangan selanjutnya, hal ini mengarah pada konstruksi ruang yang memiliki sifat derivabilitas yang persis seperti ini (ruang yang dinormalisasi). Secara khusus, telah ditunjukkan mekanika dapat diturunkan dalam ruang Euclidean dan dalam ruang gerak. Sebaliknya, ada ruang bernorma yang bukan Euclidean.
Gagasan Kant dan Newton ruang Euclidean, ruang alam, dan ruang di mana deduksi dapat dilakukan adalah identik akhirnya hilang. Metode aksiomatik pada awalnya mempunyai efek pembeda yaitu ruang-ruang yang berbeda dapat dibangun di mana aksioma-aksioma tertentu berlaku dan aksioma-aksioma lainnya tidak, yang kemudian diikuti dengan sifat-sifat ruang yang berbeda pula.
Proses aksiomatisasi sungguh luar biasa. Pada awalnya terdapat operasi matematika yang terkenal (seperti konstruksi geometri dan perhitungan aritmatika), yang dalam keadaan tertentu dapat meninggalkan area yang sebelumnya dicakup oleh aksioma. Hal ini menyebabkan didefinisikannya operasi baru (perhitungan aritmatika dalam kalkulus diferensial) yang tidak menerapkan aksioma yang dilanggar. Dan dari operasi baru tersebut, kesimpulan ditarik kembali ke aksiomatik kumpulan angka dan ini diperluas hingga mencakup aksioma yang memperbolehkan operasi baru.
Dalam bentuk akhirnya, sistem aksiomatik terdiri dari definisi yang menentukan himpunan bilangan atau titik, aksioma yang menangkap sifat dasarnya, dan operasi tentang cara membangun himpunan tersebut. Selama ini selalu terbukti adanya ketegangan antara definisi dan aksioma di satu sisi dan operasi di sisi lain. Entah karena tidak jelasnya operasi mana yang sebenarnya mungkin dilakukan (misalnya dalam geometri Euclidean pertanyaan apakah lingkaran dapat dikuadratkan), atau, seperti halnya derivasi, operasi tersebut melampaui cakupan aksioma.