Belajar dari Matematika, Setiap Masalah Pasti Ada Solusinya

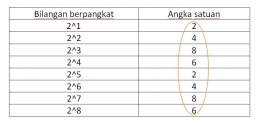
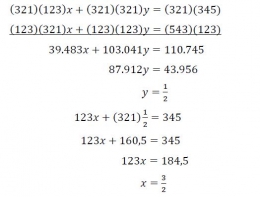Nah, kembali pada contoh di atas. Kita akan mencoba mencari angka satuan dari 2^2020 (soal nomor.2)

Perlukah kita hitung hasil dari 2^2020? 

Tentu tidak. Jika kita hitung hasilnya, pasti akan memakan waktu yang lama. Untuk soal seperti ini cukup kita amati angka satuannya, dan kita lihat polanya:

Sumber gambar: Tangkapan layar pribadi

Pada tabel tampak bahwa angka satuan membentuk pola yaitu 2,4,8,6,2,4,8,6. Berarti angka satuan dari 2^2020 adalah jatuh pada angka 6 karena 2020 bisa dibagi 4. Dalam pemecahan soal ini kita menggunakan strategi 1, yaitu menentukan pola.

Contoh lain adalah soal berikut:

Tentukan nilai x+y jika 123x + 321y = 345 dan 321x +123y = 543.

Soal ini biasanya diselesaikan dengan gabungan metode eliminasi dan subtitusi sebagai berikut: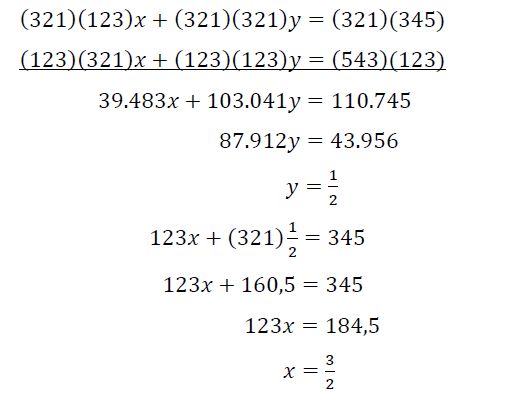

Sumber gambar: Tangkapan layar pribadi

Dan akhirnya diperoleh x+y= 3/2+ = 2. Cara yang cukup panjang dan agak rumit.

Namun dengan menggunakan sudut pandang yang berbeda, kita bisa menjumlahkan kedua persamaan tersebut dan diperoleh :

444x + 444y = 888 atau 444 (x+y) = 888. Sehingga nilai x+y=2. Selesai, benar-benar cara yang lebih efisien.

Ternyata soal matematika yang tampaknya sulit, bisa diselesaikan dengan sedikit kecerdikan dan keuletan kita.

Hampir sama dengan kehidupan, kadang kita dihadapkan pada masalah yang tampaknya demikian rumit. Namun dengan kesabaran dan keuletan pelan-pelan semua akan bisa teratasi.