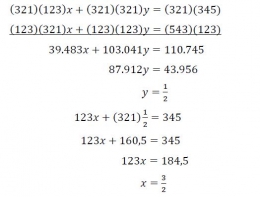Suatu saat dalam pengayaan materi bilangan bulat, saya menayangkan soal berikut di depan kelas:
Urutan hari berdasarkan pasaran kalender Jawa adalah Wage, Kliwon, Legi, Pahing, dan Pon. Jika hari ini adalah Minggu Pahing, 31 Agustus 2011, jatuh pada hari apakah 2012 hari lagi?
Siswa tertawa dan memberikan tanggapan yang beragam, "Bukankah dengan melihat kalender di HP bisa, Bu?", tanya seorang siswa.
"Oh, tentu, tapi pembelajaran kita kali ini tidak menggunakan HP," jawab saya.
Dalam beberapa materi misal statistika, saya memperbolehkan siswa menggunakan HP, tapi di beberapa materi yang lain tidak.
Bagi siswa yang suka matematika pasti akan tergelitik, dan mulai mengambil buram untuk membuat hitungan. Bagi yang tidak suka? Mereka akan saling memandang dan akhirnya pada kesimpulan, "ah soal gak jelas itu"...he.. he..
Bagaimana cara menyelesaikan soal tersebut?
- Cari KPK 5 (banyak weton) dan 7 (banyak hari), yaitu 35
- 2012: 35 = 57 sisa 17
- 17 hari setelah Minggu Pahing adalah Rabu Wage
Soal di atas adalah salah satu soal olimpiade matematika. Lantas, apa yang membedakan soal olimpiade matematika dengan soal matematika biasa?
Soal olimpiade memerlukan penalaran yang lebih, kadang untuk mencari solusinya diperlukan beberapa konsep matematika.
Coba kita bandingkan dua soal berikut:
- Tentukan hasil dari 2^4 +3^2 +5^3
- Berapakah angka satuan dari 2^2020?
Yang pertama adalah soal matematika biasa yang kedua soal olimpiade. Meskipun materinya sama yaitu bilangan berpangkat namun terasa berbeda, bukan?
Penyelesaian soal pertama cukup kita hitung masing-masing suku lalu kita jumlahkan. Dari soal pertama diperoleh 16+9+125=150.
Bagaimana dengan soal kedua?
Soal kedua tampak lebih "menggoda" daripada soal pertama, dan penyelesaiannya tidak hanya menggunakan konsep bilangan berpangkat.
Nah, solusinya akan kita bahas di bagian bawah ini.

Lalu bagaimana strategi pembinaan siswa olimpiade?
Kepada anak-anak olimpiade diberikan materi yang setingkat di atas rata-rata. Misal, pada siswa olimpiade matematika tingkat SD, akan sedikit diberi materi SMP, demikian juga untuk tingkat SMP akan sedikit diberi materi SMA.
Sebenarnya soal pada lomba semisal OSN sudah dibuat agar bisa diselesaikan dengan konsep yang sesuai. Misal soal OSN SMP pasti bisa diselesaikan dengan konsep matematika SMP atau daya nalar anak SMP. Tapi kadang karena masalah waktu, konsep yang lebih tinggi perlu diberikan supaya siswa bisa menyelesaikan soal dengan lebih cepat.
Sebagai contoh, saya memberikan materi trigonometri pada siswa olimpiade, meski materi ini baru akan mereka dapatkan di SMA.
Dengan bekal trigonometri siswa akan lebih mudah mengerjakan masalah yang berkaitan dengan segitiga.
Pada siswa olimpiade juga perlu diajarkan strategi pemecahan masalah. Ada beberapa strategi untuk menyelesaikan masalah matematika, antara lain:
- Menentukan pola
- Menggambarkan masalah
- Bekerja dari jawaban yang dikehendaki
- Membuat pemisalan yang tepat
- Membuat tabel
- Menggunakan sudut pandang yang berbeda
- Menggunakan penyelesaian untuk masalah sejenis yang lebih sederhana
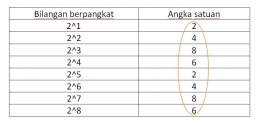
Nah, kembali pada contoh di atas. Kita akan mencoba mencari angka satuan dari 2^2020 (soal nomor.2)
Perlukah kita hitung hasil dari 2^2020?
Tentu tidak. Jika kita hitung hasilnya, pasti akan memakan waktu yang lama. Untuk soal seperti ini cukup kita amati angka satuannya, dan kita lihat polanya:

Contoh lain adalah soal berikut:
Tentukan nilai x+y jika 123x + 321y = 345 dan 321x +123y = 543.
Soal ini biasanya diselesaikan dengan gabungan metode eliminasi dan subtitusi sebagai berikut:
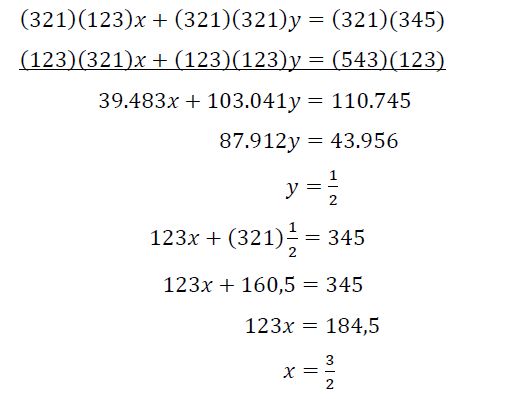
Namun dengan menggunakan sudut pandang yang berbeda, kita bisa menjumlahkan kedua persamaan tersebut dan diperoleh :
444x + 444y = 888 atau 444 (x+y) = 888. Sehingga nilai x+y=2. Selesai, benar-benar cara yang lebih efisien.
Ternyata soal matematika yang tampaknya sulit, bisa diselesaikan dengan sedikit kecerdikan dan keuletan kita.
Hampir sama dengan kehidupan, kadang kita dihadapkan pada masalah yang tampaknya demikian rumit. Namun dengan kesabaran dan keuletan pelan-pelan semua akan bisa teratasi.
Ya, matematika mengajarkan pada kita bahwa setiap masalah pasti akan ada solusinya.

Salam matematika:)
Referensi:
- Matematika 9 Kurikulum 2013 Kementrian Pendidikan dan Kebudayaan Republik Indonesia
- Modul Pembinaan Olimpiade matematika SMP oleh Ahmad Wachidul Kohar, S.Pd
Follow Instagram @kompasianacom juga Tiktok @kompasiana biar nggak ketinggalan event seru komunitas dan tips dapat cuan dari Kompasiana. Baca juga cerita inspiratif langsung dari smartphone kamu dengan bergabung di WhatsApp Channel Kompasiana di SINI