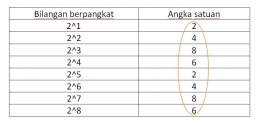
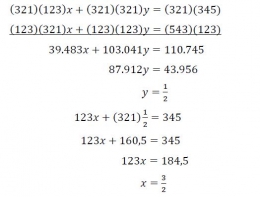Penyelesaian soal pertama cukup kita hitung masing-masing suku lalu kita jumlahkan. Dari soal pertama diperoleh 16+9+125=150.
Bagaimana dengan soal kedua?
Soal kedua tampak lebih "menggoda" daripada soal pertama, dan penyelesaiannya tidak hanya menggunakan konsep bilangan berpangkat.
Nah, solusinya akan kita bahas di bagian bawah ini.

Lalu bagaimana strategi pembinaan siswa olimpiade?
Kepada anak-anak olimpiade diberikan materi yang setingkat di atas rata-rata. Misal, pada siswa olimpiade matematika tingkat SD, akan sedikit diberi materi SMP, demikian juga untuk tingkat SMP akan sedikit diberi materi SMA.
Sebenarnya soal pada lomba semisal OSN sudah dibuat agar bisa diselesaikan dengan konsep yang sesuai. Misal soal OSN SMP pasti bisa diselesaikan dengan konsep matematika SMP atau daya nalar anak SMP. Tapi kadang karena masalah waktu, konsep yang lebih tinggi perlu diberikan supaya siswa bisa menyelesaikan soal dengan lebih cepat.
Sebagai contoh, saya memberikan materi trigonometri pada siswa olimpiade, meski materi ini baru akan mereka dapatkan di SMA.
Dengan bekal trigonometri siswa akan lebih mudah mengerjakan masalah yang berkaitan dengan segitiga.
Pada siswa olimpiade juga perlu diajarkan strategi pemecahan masalah. Ada beberapa strategi untuk menyelesaikan masalah matematika, antara lain:
- Menentukan pola
- Menggambarkan masalah
- Bekerja dari jawaban yang dikehendaki
- Membuat pemisalan yang tepat
- Membuat tabel
- Menggunakan sudut pandang yang berbeda
- Menggunakan penyelesaian untuk masalah sejenis yang lebih sederhana