Filsafat Matematika Descartes [3]

Memang benar bagian kerucut tidak pernah bebas diterima ke dalam geometri kuno, dan saya tidak peduli untuk melakukan perubahan nama yang dikonfirmasi oleh penggunaan; namun demikian, tampak sangat jelas bagi saya jika membuat asumsi biasa geometri itu tepat dan tepat, sedangkan mekanika tidak; dan jika menganggap geometri sebagai ilmu yang memberikan pengetahuan umum tentang pengukuran semua benda, maka tidak punya hak lagi untuk mengecualikan kurva yang lebih kompleks daripada kurva yang lebih sederhana, asalkan itu dapat dipahami seperti dijelaskan oleh gerak terus menerus atau dengan beberapa gerakan berturut-turut, setiap gerakan sepenuhnya ditentukan oleh gerakan sebelumnya; karena dengan cara ini pengetahuan yang tepat tentang besarnya masing-masing selalu diperoleh (G, 43).

Melihat dalam pernyataan ini ketepatan dan ketepatan geometri terkait erat dengan pertimbangan geometer tentang gerakan yang dapat dilacak secara tepat dan tepat. Yaitu, geometer dibenarkan dalam menggunakan kurva sederhana serta kurva yang lebih kompleks, selama konstruksi kurva ini berlangsung dengan gerakan "tepat dan tepat".

Descartes mengklarifikasi bagaimana sebuah kurva kompleks "dapat dipahami seperti yang dijelaskan oleh gerakan terus menerus atau dengan beberapa gerakan berturut-turut, setiap gerakan sepenuhnya ditentukan oleh mereka yang mendahului" dengan menghadirkan kompas mesolabe yang pertama kali dikembangkannya pada tahun 1619:

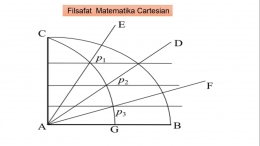
Pertimbangkan garis AB, AD, AF, dan sebagainya, yang anggap dapat digambarkan dengan menggunakan instrumen YZ [Gambar 3]. Instrumen ini terdiri dari beberapa penggaris yang disatukan sedemikian rupa sehingga YZ ditempatkan di sepanjang garis AN sudut XYZ dapat ditingkatkan atau dikurangi ukurannya, dan ketika sisinya disatukan, titik B, C, D, E, F, G, H, semua bertepatan dengan A; tetapi ketika ukuran sudut bertambah, penguasa BC, diikat pada sudut kanan ke XY di titik B, mendorong ke arah Z penguasa CD yang meluncur sepanjang YZ selalu di sudut kanan.

Dengan cara yang sama, CD mendorong DE yang meluncur sepanjang YX selalu sejajar dengan BC; DE mendorong EF; EF mendorong FG; FG mendorong GH, dan sebagainya. Dengan demikian dapat membayangkan tak terbatas penguasa, masing-masing mendorong yang lain, setengah dari mereka membuat sudut yang sama dengan YX dan sisanya dengan YZ.

Sekarang ketika sudut XYZ dinaikkan, titik B menggambarkan kurva AB, yang merupakan lingkaran; sedangkan persimpangan dari penguasa lainnya, yaitu, titik D, F, H menggambarkan kurva lainnya, AD, AF, AH, di mana yang terakhir lebih kompleks daripada yang pertama dan ini lebih kompleks daripada lingkaran.

Namun demikian saya tidak melihat alasan mengapa deskripsi dari yang pertama tidak dapat dipahami dengan jelas dan sejelas itu dari lingkaran, atau setidaknya sebagai bagian dari kerucut; atau mengapa yang kedua, ketiga, atau lainnya yang dapat dengan demikian dijelaskan, tidak dapat dengan jelas dipahami sebagai yang pertama: dan karena itu saya tidak melihat alasan mengapa mereka tidak boleh digunakan dengan cara yang sama dalam penyelesaian masalah geometris (G, 44--47).

Beberapa poin patut ditekankan. Pertama, Descartes menyajikan kurva yang lebih kompleks yang dihasilkan oleh kompasnya seperti yang dijelaskan oleh gerakan yang dapat "dipahami dengan jelas dan berbeda" seperti gerakan yang diperlukan untuk membangun lingkaran yang lebih sederhana. Dan karena gerakan jelas dan berbeda yang diperlukan untuk konstruksi mereka, kurva ini secara geometris sah.

Artinya, konsisten dengan kriteria umum Descartes untuk membangun kurva geometris, kurva kompleks ini dapat digunakan dalam solusi masalah geometris. Kedua, melihat meskipun Descartes berhati-hati untuk membedakan keprihatinan geometri dari orang-orang mekanik, ia tidak menjauhi konstruksi kurva dengan menggunakan instrumen.

Meskipun konstruksi instrumental adalah konstruksi mekanis, mereka tetap dapat memunculkan kurva geometris justru karena gerakan instrumen dikandung dengan "jelas dan jelas". gerakan dihasilkan oleh instrumen tidak membuat kurva yang dihasilkan non-geometris. (Untuk lebih lanjut tentang penggunaan instrumen di La Geometrie)

Dalam nada yang sama, kurva yang non-geometris menurut standar Descartes adalah kurva yang membutuhkan gerakan yang lebih rumit, kurang jelas dan berbeda untuk konstruksinya. Dia menjelaskan: