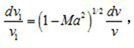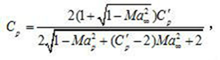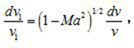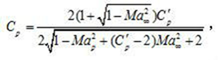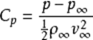Di tahun itu, dalam paper makalah berjudul “Rocket”, dimana Qian menggambarkan ambisi tingginya dengan menuliskan puisi berikut: “Dalam malam musim panas yang cerah, memandang bintang dilangit yang bergemerlapan, ada persaan kecewa yang tak tersentuh, apakah memang benar begitu menyedihkan? Ohh tidak, tidak pernah., Kita harus menaklukkan alam semeseta.” (“你在一个清朗的夏夜,望着繁密的闪闪群星,有一种不可及的失望吧,我们真的如此可怜吧,不 绝不,我们必须征服宇宙” : “In a clear and bright summer night, looking up at the dense shining stars, you feel a kind of untouchable disappointment. Are we really so pathetic? No. never. We must conquer the universe.”)
Di MIT, Qian yang perfeksionis ini selalu top dalam kelasnya, setiap pagi bangun jam 6. Kecuali ke kelas kuliah dan eksprimen, sebagian besar waktunya berada di perpustakaan. Hobinya adalah musik klasik. Boston Symphony Ochestra total mengadakan 20 kali konser dari tahun 1935-1936, Qian tidak pernah abstain sekalipun.
Dalam waktu kurang dari setahun setelah tiba di AS, Qian yang berumur 25 tahun ini melakukan perjalanan melintas kontinental AS dan datang ke Caltech (Calfifornia Institute of Technology) seorang diri, untuk bertemu dengan seorang mentor yang paling penting dalam hidupnya---Theodore von Karman seorang legendaris ilmuwan Yuhudi yang datang ke AS untuk menghindarianti-Semitisme di Jerman pada waktu itu, dan bersama von Karman melakukan studi penerbangan.
Sama sebagai pendatang dari negara lain antara von Karman dan Qian Xuesen para jenius mmepunyai perasaan saling simpati.
Mentornya von Karman dalam buku kenangannya menggambarkan ketika pertama kali bertemu Qian: “Ketika aku mendongak untuk mengamati seorang pemuda yang sedikit pendek dengan tatapan serius, dan menjawab pertanyaan saya dengan jawaban yang sangat presisi, sehingga membuat saya langsung terkesan dengan kecepatan dan ketajaman pikirannya.”

Karman-Tsien(Qian) Pressure Volume Law
The velocity potential equation of the two-dimensional non-viscous steady subsonic velocity is a nonlinear partial differential equation in the physical plane (x, y). By proper transformation, the linear equation can be formed on the velocity plane (Vx, Vy), but the boundary condition is to be solved, it is difficult to solve the problem. In order to solve this difficulty, Qian Xuesen proposed a "tangential gas approximation" method. The main point is that the isentropic curve of the passing point (poo.1/poo) is replaced by a tangent line at (poo.1/poo) , in the plane of the reciprocal of pressure and density 1, Flow pressure and density. The introduction of a hypothetical incompressible flow (see compressible flow) between the velocity i and the velocity in the original subsonic flow satisfies the relationship: