Pelajaran Penting yang Bisa Diambil dari Teori Himpunan

Pelajaran kehidupan apa yang bisa diambil dari matematika? Banyak, satu diantaranya adalah toleransi. Toleransi  adalah sikap manusia untuk saling menghormati dan menghargai perbedaan, baik antar individu maupun kelompok. Betapa pentingnya menanamkan  toleransi untuk menghadirkan perdamaian dalam keberagaman.

Bagaimana matematika bisa menanamkan toleransi? Tulisan saya kali ini akan mencoba menjawabnya.

Satu materi matematika yang dipelajari di kelas 7 semester 1 adalah himpunan. Materi himpunan seolah mengajak siswa kembali ke masa awal SD dimana mereka diajak belajar matematika dengan gambar yang bermacam-macam.

Dalam pembelajaran materi ini, siswa selalu antusias saat diminta untuk menyebutkan contoh-contoh himpunan. Jawaban mereka sangat beragam tak ubahnya seperti zaman saya sekolah dulu.

Dulu saat siswa diminta menyebutkan contoh himpunan, yang paling sering muncul adalah himpunan warna pelangi, himpunan binatang ternak, himpunan binatang yang berkembang biak dengan bertelur atau himpunan warna lampu lalu lintas. 

Namun kini contoh siswa lebih bervariasi. Meski himpunan hewan berkaki empat, hewan unggas tetap keluar, namun ada juga contoh menarik lain yaitu himpunan stasiun televisi di Indonesia, himpunan sosmed yang banyak dipakai, atau himpunan nama- nama merk HP. Hmm.. zaman benar benar sudah berubah.

Pelajaran himpunan di TK dan SD, dokumentasi pribadi

Teori Himpunan

Himpunan adalah kumpulan obyek yang sifat keanggotaannya didefinisikan dengan jelas.

Jelas disini berarti sudah ada patokan yang sama untuk setiap orang. Contoh kumpulan yang merupakan himpunan adalah kumpulan bunga yang berwarna merah, kumpulan binatang berkaki dua juga kumpulan warna pelangi.

Bandingkan contoh di atas dengan  kumpulan bunga yang indah, kumpulan artis yang cantik dan kumpulan binatang yang lucu.

Kumpulan tersebut bukan himpunan karena indah menurut satu orang belum tentu indah menurut orang lain. Demikian pula untuk cantik dan lucu, setiap orang mempunyai standar yang berbeda.

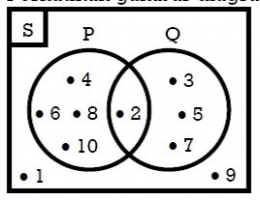
Dalam himpunan dikenal himpunan semesta. Semesta adalah himpunan yang memuat anggota himpunan yang dibicarakan. Sebagai contoh jika terdapat himpunan P ={2,4,6,8,10}, Q={2,3,5,7} dan S={1,2,3,4,5,6,7,8,9,10} . S adalah himpunan semesta karena semua anggota P dan Q termuat dalam S.

Hubungan antara himpunan P, Q dan S bisa digambarkan dalam diagram Venn sebagai berikut:

Sumber dokumentasi pribadi

Dari diagram bisa diketahui ada anggota P yang juga berupakan anggota Q dilambangkan dengan P irisan Q, ada anggota P yang tidak termasuk P dilambangkan dengan P-Q, ada anggota Q yang tidak termasuk P, dilambangkan dengan Q-P, gabungan dari P dan Q atau PUQ juga anggota S yang tidak termasuk dalam P maupun Q dilambangkan dengan (PUQ)' (baca: P gabungan Q komplemen).

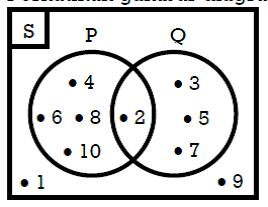
Jika dituliskan dengan menggunakan tanda operasi himpunan menjadi :

P irisan Q    = {2}

P - Q    = { 4,6,8,10}

Q -- P   = {3,5,7}

P U Q  = { 2,3,4,5,6,7,8,10}

(PUQ)' = {1,9}

Penggambaran hubungan antar himpunan dalam diagram Venn bisa dianalogikan dengan apa yang terjadi dalam kehidupan sehari-hari. Dalam keseharian manusia biasa membuat kelompok berdasarkan kesamaan-kesamaan yang dimiliki. Misalnya kesamaan visi, kesenangan, profesi atau apa saja.

Ada yang mengikatkan diri pada satu kelompok, dua kelompok, ataupun banyak kelompok. Namun ada pula yang tidak suka mengikatkan diri pada kelompok manapun. Salahkah? Tentu tidak. Karena setiap orang memiliki pandangan yang berbeda dan bebas melaksanakan apa yang diyakininya sejauh tidak berbenturan dengan aturan. Melalui pelajaran himpunan siswa bisa belajar tentang kemajemukan dalam masyarakat dan menghargainya.

Ada hal lain yang bisa diambil dari pembelajaran himpunan. Suatu saat saya memberikan soal sebagai berikut:

Berapakah nilai x yang memenuhi x +2 <2?
Meski bukan soal himpunan, soal tersebut masih berkaitan dengan himpunan.

Setelah mengerjakan dalam beberapa saat ternyata ada dua versi jawaban yang muncul dari siswa. Siswa pertama menjawab tidak ada jawaban atau himpunan kosong, sementara siswa yang lain menjawab {-1,-2,-3,..}.

"Dua duanya benar", kata saya saat itu.

Beberapa siswa protes," Kok bisa benar semua Bu?"

Dengan rinci saya jelaskan bahwa siswa pertama benar, karena ia menjawab dengan semesta bilangan positif. Tidak ada bilangan positif yang jika ditambah dua hasilnya lebih kecil dari dua.
Siswa kedua juga tidak salah, karena ia menjawab dengan semesta bilangan bulat. Bilangan bulat yang jika ditambah dua hasilnya kurang dari dua adalah adalah {-1,-2,-3,..}.
Bukankah  pembuat soal tidak mencantumkan semesta pembicaraannya? 

Siswa tampak lega mendengar jawaban itu.

Penanaman toleransi sejak dini, Sumber gambar: detikNews-detik.com

Apa pelajaran penting yang bisa diambil dari masalah ini? Jangan mudah antipati terhadap pandangan orang yang berbeda dengan kita karena tiap orang punya pijakan atau semesta berpikirnya sendiri-sendiri. Perbedaan adalah sebuah keniscayaan dan perlu sikap bijak dalam menghadapinya.

Semoga bermanfaat.

Salam matematika