Di awal tulisan ini saya mengajak pembaca untuk mencermati tiga soal matematika berikut ini:
[Soal nomor 1] Ibu mempunyai 75 butir permen. Permen-permen itu hendak dibagikan pada 5 orang anaknya. Berapa bagian tiap anak?
[Soal nomor 2] Menjelang lebaran, sebuah toko pakaian mengadakan diskon besar-besaran untuk semua produk kemeja dan celana. Pak Hakim membeli sebuah kemeja seharga Rp 125.000 dan sebuah celana Rp 150.000. Jika toko memberikan diskon 15.23% per item, berapakah harga yang harus dibayar Pak Hakim?
[Soal nomor 3] Sebuah tangga disandarkan di tembok dengan posisi miring. Jika panjang tangga 25 m dan jarak ujung bawah tangga ke tembok adalah 15 m, berapakah jarak ujung atas tangga dari lantai?
Soal yang saya ambil di atas biasa muncul di soal-soal latihan matematika tingkat SD dan SMP.
Nah, mari kita bahas satu per satu.
Soal nomor 1 adalah soal materi pembagian dengan cara penyelesaian yang sangat simpel, yaitu 75:5=15, jadi bagian tiap anak adalah 15 butir permen.

Penyelesaiannya adalah (100-15.23)% x 275.000 = 84.77% x 275.000 = 233.117,5. Jadi harga baju dan celana yang harus dibayar Pak Hakim adalah Rp 233.117,5.
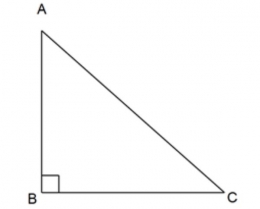
Soal nomor 3, sering dijumpai di materi Pythagoras. Soal tersebut bisa digambarkan sebagai berikut, misalkan AC adalah tangga, AB adalah dinding dan BC adalah lantai.
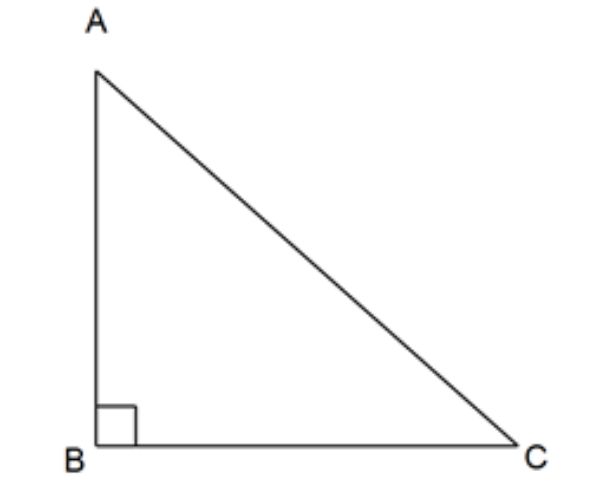
Untuk mencari jarak ujung atas tangga dengan lantai berarti kita mencari panjang AB. Dengan menggunakan teorema Pythagoras diperoleh:
AB^2 = AC^2 - BC^2
= 25^2 - 15^2
= 625 - 225 = 400
AB = 400 = 20
Jadi jarak ujung atas tangga ke lantai adalah 20 m.
Secara matematika tidak ada yang aneh dengan soal di atas, tapi logiskah?
Dari soal nomor satu saya pernah mendapat komentar siswa. Setengah bercanda siswa saya berkata, "Ibunya jahat ya, bu? Kan bisa gigis (Jawa: gigi keropos) semua gigi anak-anaknya."
Sontak siswa dalam kelas semua tertawa termasuk saya. Pintar sekali murid saya ini, ibu mana yang mau mengorbankan gigi anak-anaknya dengan memberikan permen sebanyak itu.
Pada soal nomor dua sekilas tidak ada masalah, tapi coba kita amati besaran diskonnya. Kenapa sulit sekali ya?
Biasanya besaran diskon yang diterapkan di toko adalah berupa bilangan bulat. Kalau pun pecahan, maka yang digunakan adalah sekian koma lima.
Soal tersebut kelihatan mengada-ada. Dengan diskon sebesar 15.23% sepertinya memaksa siswa untuk "bekerja keras" mencari hasilnya. Ya, akhirnya sebagian siswa lari ke kalkulator.
Kalau tujuan pembelajaran adalah siswa bisa mencari harga sesudah diskon lebih baik prosentase disajikan dalam bilangan yang lebih sederhana supaya pikiran siswa tidak terpecah dan akhirnya justru sibuk pada perhitungan yang rumit.
Nah untuk soal nomor tiga, saya punya sedikit cerita. Suatu saat listrik di rumah bermasalah sampai saya harus menelepon pihak PLN.
Oleh teknisinya, karena harus membetulkan di atas, kami diminta untuk menyediakan tangga. Bergegas kami meminjam tangga pada pak tukang yang tak jauh rumahnya dari tempat kami.
"Pakde, ngapunten mau pinjam tangga," kata saya.
"Boleh ambil saja, tapi itu cuma 2.5 meter ya..," kata pak tukang.
"2.5 meter itu seberapa?", tanya saya lagi.
"Ah, paling setinggi talang itu," jawab pak tukang sambil menunjuk talang di rumahnya yang tingginya sama dengan rata-rata tinggi rumah di kampung.
Deg, saat itu juga saya langsung ingat soal Pythagoras saya. 2,5 meter sudah setinggi itu, padahal di soal panjang tangga saya 25 meter.
Astaga, lha kalau disandarkan di tembok setinggi apa temboknya? Tentunya ruangan yang dibutuhkan untuk menyimpan tangga tersebut besar sekali.
Tapi saya juga heran, kenapa siswa saya tidak ada yang protes dengan soal tersebut. Jangan-jangan mereka takut pada saya. Atau sama tidak telitinya dengan saya?
Beragam perasaan berkecamuk dalam hati saya. Malu, menyesal dan gemas pada diri sendiri. "Kok gak mikir ya", kata hati saya.
Dalam pembelajaran matematika betapa seringnya kita menghadapi soal yang kurang logis semacam ini, baik mengenai bilangan atau ceritanya.
Mungkin ada yang berpendapat apa pengaruhnya soal logis atau tidak, yang penting konsep matematika yang diajarkan sudah tersampaikan, cukup kan? Ternyata masalahnya tidak sesederhana itu
Membuat soal yang kurang logis pada siswa akan berdampak siswa mempunyai pandangan bahwa matematika hanya ilmu menghitung saja.
Ia adalah ilmu yang berada di awang-awang dan punya dunia sendiri, padahal kenyataannya tidak demikian, bukan?
Matematika ada begitu dekat dengan kita, sepertinya tidak ada aspek kehidupan yang lepas dari matematika.
Dalam dunia perdagangan, memasak, teknik, jahit menjahit, dan lainnya selalu ada matematika. Kita tak pernah bisa lepas dari matematika karena selalu ada bilangan di sana.
Membuat soal yang tidak logis justru menjauhkan siswa dari matematika yang bisa berakibat mereka tidak menyukai matematika.
Membuat soal logis adalah sebuah tantangan. Di samping karena siswa sekarang semakin kritis, mereka begitu berani bertanya dan juga mempersiapkan siswa menghadapi AKM. Seperti diketahui soal yang disajikan di AKM adalah soal yang nyata dalam kehidupan sehari hari.
Lalu bagaimana agar soal yang kita sajikan logis?

Jika di pasar harga beras perkilo Rp 11.000, jangan sampai membuat soal yang di hasil akhirnya sampai pada kesimpulan Jadi harga beras yang dibeli ibu adalah Rp 120.000/kg. Eh, beras yang seperti apa itu?
Kedua, membuat soal dalam sebuah tim. Dalam sebuah tim pembuat soal, ada pembuat dan penelaah soal.
Sebelum disajikan diusahakan soal sudah ditelaah terlebih dahulu apakah soalnya tidak keluar dari kompetensi yang hendak dicapai dan juga apakah sesuai dengan kenyataan sehari-hari. Membuat soal dalam sebuah tim hasilnya jauh lebih bagus daripada bekerja sendirian.
Perlu kehati-hatian dalam membuat soal matematika. Karena logis atau tidaknya soal sangat besar pengaruhnya pada cara pandang siswa tentang matematika.
Adalah hal yang sangat aneh jika dalam pembelajaran matematika soal yang disajikan tidak logis, karena matematika sendiri mengajar siswa untuk dapat berpikir logis.
Semoga bermanfaat dan salam matematika:)
Referensi : Buku Matematika Kelas 7 dan kelas 8 Kurikulum 2013 Kementrian Pendidikan dan Kebudayaan Republik Indonesia
Baca konten-konten menarik Kompasiana langsung dari smartphone kamu. Follow channel WhatsApp Kompasiana sekarang di sini: https://whatsapp.com/channel/0029VaYjYaL4Spk7WflFYJ2H