Suatu hari seorang teman mengirimkan quotes lewat whatsapp pada saya: Love is like pi, it is natural irrational and very important.
Aha..Saya benar benar tergelitik membaca quotes ini. Siapa yang tidak kenal pi? Sejak SD tentunya kita sudah mengenalnya. Pi pertama kali dikenalkan pada materi lingkaran, tepatnya keliling lingkaran. Tiba-tiba saya langsung ingat pembelajaran saya tentang mencari nilai pi.
1. Tentang Pi
Pi adalah rasio keliling lingkaran dengan diameternya dan dilambangkan dengan huruf Yunani kecil yang berasal dari huruf pertama dari kata Yunani perimetros atau yang disebut dengan keliling.
Dari perbandingan π=K/d , akhirnya kita memperoleh rumus keliling lingkaran sebagai K=π.d. Pendekatan untuk nilai pi adalah 3,14 atau 22/7 .
Sejak jaman dahulu, para cendekiawan dan ahli matematika telah terpesona oleh pi dan telah berusaha keras untuk mendapatkan nilai pi yang paling mungkin.
1680 SM: nilai tertua pi yang telah ditemukan adalah karya orang Babel. Mereka berusaha mencari nilai pi dengan menggunakan segi enam. Nilai perkiraan phi saat itu adalah 3 + 1/8 = 3.125
1650 SM: Papirus Matematika Rhind yang ditemukan pada tahun 1855 menyebutkan bahwa orang Mesir mempelajari nilai pi dengan menggunakan segi delapan. Nilai pi diperoleh sekitar 3,16.
700 SM: Teks India Shatapatha Brahmana memberikan perkiraan pi sama dengan 25/8 (3.125). Matematikawan India dari periode Veda kembali memperkirakan Pi menjadi 3,1416 dengan menggunakan perhitungan astronomi.
Archimedes (287 SM-212 SM) dianggap sebagai orang pertama yang menghitung estimasi Pi yang akurat dengan mencari keliling poligon segi 96.
Perkiraan nilai pi menurut Archimedes adalah 220/71<π<22/7
Sesudah Archimedes banyak ahli matematika akan menggunakan metode sejenis untuk menentukan semakin banyak digit Phi. Dari perkiraan nilai phi sampai 5 tempat desimal, 6 tempat desimal, 14 tempat desimal hingga saat ini, komputer yang paling kuat mampu menentukan hingga 13 triliun tempat desimal.

2. Pembelajaran untuk mencari nilai pi
Suatu saat saya bertanya pada siswa,"Berapakah nilai pi?"
Kompak mereka menjawab,"3.14 atau 22/7!".
"Dari mana itu?" tanya saya lagi. Siswa sejenak ragu. Akhirnya ada yang menjawab. "Dari guru SD saya, Bu.."
He.. He... Benar sekali, tapi tentunya bukan itu maksud saya.
Dalam pembelajaran materi Lingkaran di kelas 8, saya ingin memantapkan pemahaman siswa bahwa phi adalah hasil pembagian antara keliling lingkaran dan diameternya. Jadi mereka faham asal muasal pi. Tidak sekedar hafal.
Sehari sebelumnya tiap siswa saya minta untuk membawa satu benda berbentuk lingkaran dan mistar dari rumah. Dalam pembelajaran siswa saya minta untuk mengukur diameter dan keliling lingkaran dan hasilnya dimasukkan dalam tabel yang sudah disediakan.

"Bagaimana cara mengukur keliling benda ini sementara yang tersedia adalah mistar?" tanya saya sambil membawa sebuah mistar dan tutup toples.
Sejenak siswa berpikir. Ada beberapa siswa yang mencoba menekuk mistar plastik mengikuti bentuk lengkungan lingkaran dan gagal.
Setelah beberapa lama, ternyata ada dua versi cara yang muncul. Yang pertama mengambil benang, tali atau pita lalu dililitkan pada benda berbentuk lingkaran satu kali , panjang benda yang dililitkan tadi diukur dengan mistar, itulah keliling lingkaran.

Yang kedua dengan menggelindingkan benda di atas penggaris. Sebelumnya benda ditandai dengan spidol dan digelindingkan mulai dari angka nol. Sesudah satu kali penggelindingan, dilihat tanda spidol berhenti di angka berapa, dan itulah kelilingnya.

Cukup menarik. Siswa jadi mempunyai banyak ide untuk melakukan sesuatu jika sarananya terbatas.
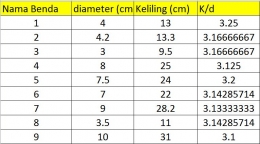
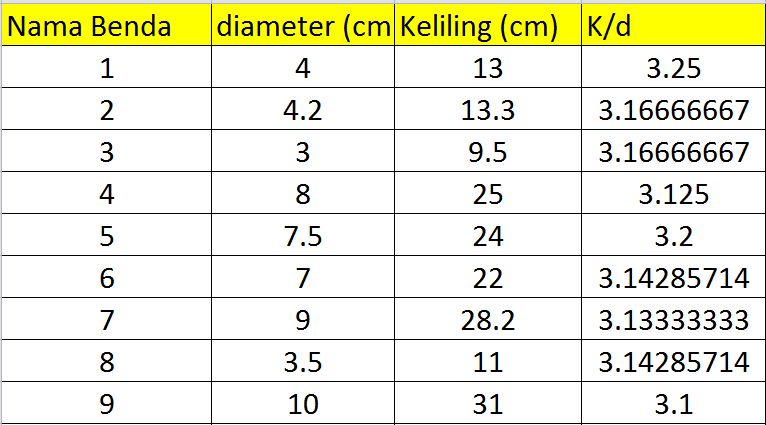
Sesudah pengukuran, siswa diminta memasukkan data dalam tabel yang ditayangkan guru di ppt. Tabel berisi kolom untuk ukuran diameter (d), keliling(K) dan keliling /diameter(K/d).
Nah, siswa diminta mengamati kolom K/d. Tampak bahwa hasilnya selalu 3 koma sekian. Jika percobaan dilakukan dengan teliti dan berulang-ulang maka nilai K/d akan semakin mendekati 3.14 atau pi.
Nah kembali ke quotes: Love is like pi, it is natural irrational and very important. Benarkah? Important? jelas, pi amat penting. Banyak perhitungan yang memerlukan nilai pi. lrrational? jelas. Bilangan irasional adalah bilangan yang jika dinyatakan dalam bentuk desimal angka di belakang koma tidak beraturan dan tidak berhenti. Bahkan dari uraian di atas sampai 13 triliun angka di belakang koma, dan mungkin masih bisa bertambah lagi.
Natural? Bukan, pi jelas bukan bilangan natural atau bilangan asli, bilangan asli adalah bilangan bulat lebih dari nol, sementara pi adalah 3.14. Ia jelas bukan bilangan asli. Yang lebih tepat menurut saya pi adalah bilangan real. Bilangan real terbagi menjadi dua yaitu bilangan rasional dan irasional. Karena pi irasional jelas ia bilangan real. Jadi quotes yang lebih tepat adalah Love is like pi, it is real, irrational and very important.
Lalu apakah cinta seperti pi? Apakah cinta itu nyata? Irasional? Sangat penting dalam kehidupan? he..he..Saya pikir sahabat kompasianer pasti lebih memahaminya.
Salam matematika :)
Sumber bacaan : Matematika 8 Kurikulum 2013 Departemen Pendidikan dan Kebudayaan
Baca konten-konten menarik Kompasiana langsung dari smartphone kamu. Follow channel WhatsApp Kompasiana sekarang di sini: https://whatsapp.com/channel/0029VaYjYaL4Spk7WflFYJ2H