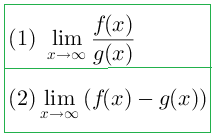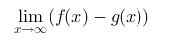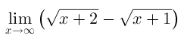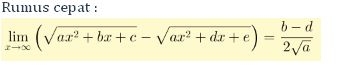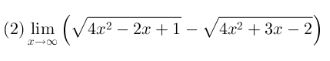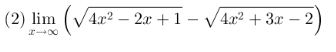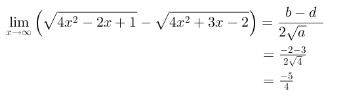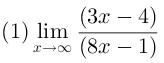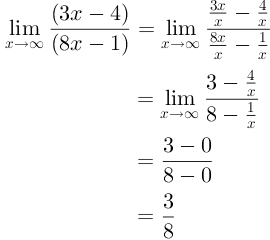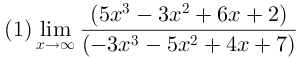Semangat pagi
Saya Sri Nurhaida dari kelas XII TKI B sekolah di SMK Negeri 1 Wanareja akan sedikit berbagi tips dan trik menyelesaikan soal limit fungsi aljabar tak tentu
Oke langsung aja yah
Dalam bahasa matematika untuk menyatakan suatu keadaan atau kondisi yang nilai dan besarnya tidak dapat ditentukan digunakan lambang∞(dibacanya tak berhingga). Soal-soal limit fungsi aljabar dengan variabel atau peubah x mendekati tak berhingga, biasanya sering dijumpai dalam bentuk umum seperti dibawah ini:
Bentuk umum limit fungsi aljabar x mendekati tak berhingga adalah,
adapun cara lainya adalah :
Mengalikan dengan faktor lawan
biasanya rumusnya berbentuk

contoh soalnya:

pertama kita keerjakan dengan cara yang umum dulu ya

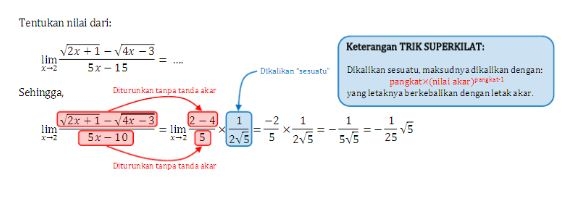
selain itu kita juga bisa menghitung nilai limit fungsi aljabar bentuk lim yaitu dengan syarat f(x) dan g(x) merupakan fungsi kuadrat. Rumusnya seperti ini :

perhatikan contoh berikut:

penyelesaian:

b = -2 ,dan d= 3,dan a= 4.. maka kita gunakan rumus cepat diatas

yang kedua yaitu dengan cara L’Hopital
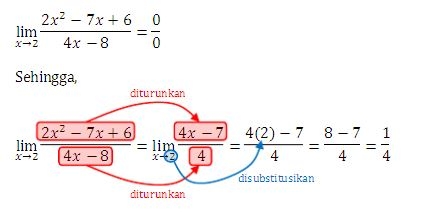
contohnya:

dan ini cara cepatnya:

contoh lainnya

Perhatikan f(x) dan g(x) mempunyai pangkat tertinggi yaitu 1, maka pembilang dan penyebut masing-masing dibagi x, maka

cara cepatnya:
Dari soal diatas, pangkat tertinggi f(x) =pangkat tertinggi g(x) yaitu pangkat 3 maka memenuhi (1) jadi

nah, lebih cepat kan
sekian dari saya apabila ada kekurangan mohon maaf ya
sampai jumpa :)
Baca konten-konten menarik Kompasiana langsung dari smartphone kamu. Follow channel WhatsApp Kompasiana sekarang di sini: https://whatsapp.com/channel/0029VaYjYaL4Spk7WflFYJ2H