Contoh : XDani = TDani + EDani
- Xj = Tj + Ej
Persamaan tersebut digunakan jika pengukuran dilakukan pada sampel individu, dengan beberapa kali sesi (trial) pengukuran, dengan j adalah sesi pengukuran.
Contoh :
XMalam = TMalam + EMalam
XPagi = TPagi + EPagi
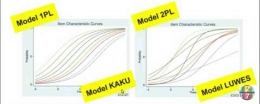
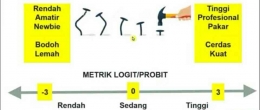
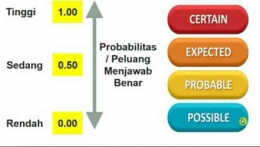
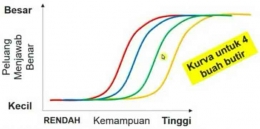
TEORI RESPONS BUTIR
Teori Respons Butir merupakan sebuah teori yang berupaya untuk memadukan subjek dan butir menjadi satu informasi dalam satu skala. Hal ini dikarenakan pada CTT tidak dapat meletakkan subjek dan butir dalam 1 skala. Misalkan :
- Tingkat kesulitan butir (P) : P Butir-1 = 0,5 dan Butir-2 = 0,3.
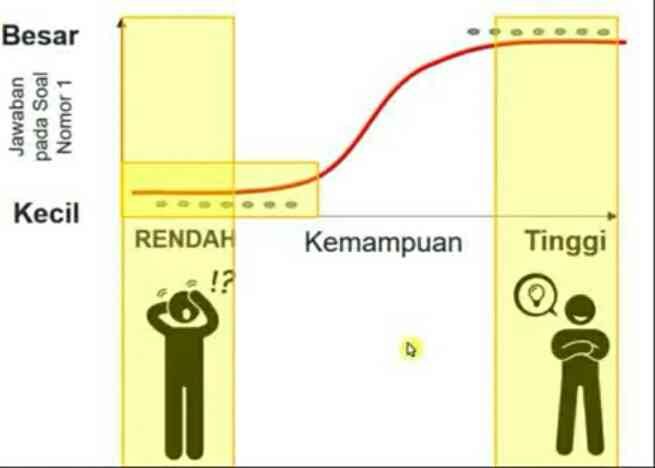
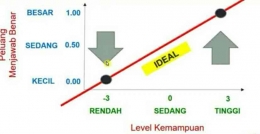
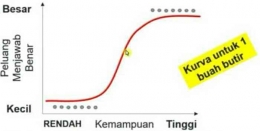
Belum tentu butir-butir tersebut berbeda tingkat kesulitannya. Hal ini dikarenakan tingkat kesulitan butir itu dipengaruhi oleh subjek. Soal akan terasa sulit jika diberikan kepada orang-orang yang kemampuannya rendah, sebaliknya soal akan terasa mudah jika diberikan kepada orang-orang yang kemampuannya tinggi.
- Hasil pemaduan antara subjek dan butir itu nantinya akan meletakkan keduanya menjadi sesuatu yang bersifat invarian atau konsisten antar subjek dari berbagai macam level.
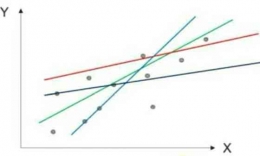
Untuk memahami Teori Respons Butir secara lebih lanjut, terlebih dahuulu kita perlu memahami dan mengenal Analisi Regresi Linier. Adapun persamaan dari regresi Linier yaitu : Y = B0 + B1X + E

Parameter
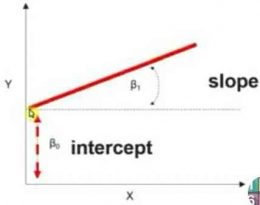
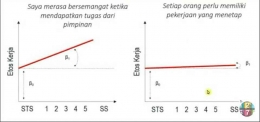
B0 = intersep
B1 = Slope/Kemiringan
Intersep adalah kondisi ketika B1 = 0.
- Menunjukkan peranan X terhadap perubahan Y.
- Semakin besar kemiringannya, semakin besar peranan X terhadap Y.
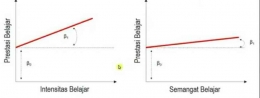
- Dalam psikometrika, slope dapat menunjukkan korelasi butir total
Gambaran tentang parameter intersep: