Simulasi Monte Carlo dengan Excel

Metode Monte Carlo merupakan metode dimana kita men-generate banyak percobaan (simulasi) untuk mendapatkan expected value (nilai harapan) dari suatu peubah acak. Di dalam simulasi ini kita men-generate angka random dari suatu distribusi yang kita tentukan di awal. Monte Carlo dahulu sering digunakan dalam permainan judi casino karena membantu dalam memprediksi suatu nilai.

Kita dapat menemukan metode Monte Carlo diaplikasikan dalam berbagai bidang, mulai dari ekonomi sampai fisika nuklir dan juga lintas bidang. Tentu saja cara aplikasinya berbeda dari satu bidang ke bidang lainnya, dan ada banyak sekali himpunan bagian Monte Carlo meskipun dalam satu bidang yang sama.

Monte Carlo umumnya digunakan dalam dunia keuangan dan perbankan, untuk menghitung resiko finansial. Salah satu kegiatan dalam dunia perbankan yang kita ketahui bersama adalah pemberian kredit kepada nasabah. Peranan Monte Carlo dalam hal ini yaitu untuk memprediksi risiko finansial perbankan akibat kredit macet. 

Dalam dunia investasi, simulasi Monte Carlo dapat digunakan oleh investor untuk mengetahui resiko gagal bayar dari suatu instrumen investasi. Oleh karena itu, simulasi Monte Carlo sangat membantu dalam melakukan mitigasi risiko. 

Hal yang menyamakan semua pengaplikasian di berbagai bidang tersebut adalah bahwa percobaan Monte Carlo membangkitkan bilangan acak untuk memeriksa permasalahan.

Tersedia banyak commercial packages untuk menjalankan simulasi Monte Carlo. Bagaimanapun program spreadsheet dasar juga dapat digunakan untuk menjalankan suatu simulasi, salah satunya Microsoft Excel. Beberapa percobaan dapat di-generate dengan beberapa formula dasar sebanyak jumlah iterasi yang disyaratkan oleh model.

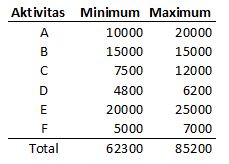
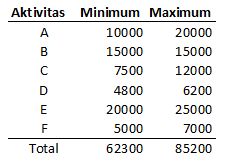
Dalam percobaan kali ini, asumsikan terdapat suatu proyek yang terdiri atas enam aktivitas. Setiap aktivitas mempunyai total biaya dalam range tertentu. Dari semua aktivitas tersebut, terdapat aktivitas dengan biaya yang fix (aktivitas B), namun secara keseluruhan nilai-nilainya berada pada suatu interval. Monte Carlo akan digunakan untuk mengestimasi total biaya dari proyek. Asumsi yang penting dan tidak boleh dilupakan adalah variabel-variabel harus saling independen. Dengan kata lain, biaya dari masing-masing aktivitas tidak dipengaruhi oleh biaya dari aktivitas lain.

DOK.ISTIMEWA

Total biaya proyek merupakan random variable yang nilainya jatuh di antara nilai maksimum dan nilai minimum. Variabel ini akan mengikuti distribusi normal ketika ia merupakan gabungan dari banyak random variabel. Inilah sebabnya mengapa individual distribution dari variabel tidaklah penting.

Prosedur umum dari metode Monte Carlo adalah sebagai berikut.

1.  Generate angka random yang mewakili biaya untuk tiap aktivitas.
2. Jumlahkan setiap seri angka random dari seluruh aktivitas untuk memperoleh total biaya proyek.
3. Expected cost proyek adalah rata-rata dari total biaya proyek hasil penjumlahan.

Di sini saya menggunakan aplikasi Microsoft Excel 2013. 

Langkah pertama yaitu men-generate angka random untuk biaya setiap aktivitas. Asumsikan biaya berdistribusi uniform. Kita gunakan fungsi RAND() untuk membangkitkan angka random pada interval (0,1) kemudian kita kalikan dengan range dari tiap aktivitas. Range adalah selisih antara nilai maksimum dan nilai minimum.

Biaya random untuk aktivitas A dapat kita tulis formulanya seperti berikut.

=RAND()*(20000-10000)+10000

Formula ini akan men-generate angka random yang nilainya antara 10000 dan 20000.

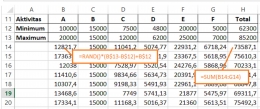
Jika formula di atas kita terapkan untuk setiap aktivitas, biaya total proyek merupakan penjumlahan dari fungsi untuk semua aktivitas. Kemudian kita terapkan ke semua baris sebanyak iterasi model. 

Gambar di bawah ini merupakan sampel dari model yang menunjukkan tujuh iterasi pertama. 

DOK.ISTIMEWA

Menentukan jumlah iterasi

Metode Monte Carlo dapat memprediksi expected value dari peubah acak sekaligus juga mampu memprediksi estimation error, yang proporsional atau sebanding dengan banyaknya iterasi. Rumus total error yaitu : 

error = (3*sigma)/(akar N)

dimana sigma adalah standar deviasi dari peubah acak, dan N adalah jumlah iterasi. Kita dapat meng-estimasi batas atas dari sigma dengan menghitung standar deviasi dari nilai maksimum, minimum, dan rata-rata peubah acak.

sigma =STDEVP(H12:H13;AVERAGE(H12:H13)) = 9349

Mari kita tentukan jumlah iterasi yang diperlukan untuk error kurang dari 2%. Estimasi kasar peubah acak adalah rata-rata dari nilai maksimum dan nilai minimum. Absolute error 2% adalah rata-rata nilai maksimum dan minimum dibagi dengan 50 (100/2) :

error =AVERAGE(H12:H13)/50 = 1475

Sehingga jumlah iterasi untuk mendapatkan hasil dengan error kurang dari 2% adalah:

N = (3*9349/1475)^2 = 362

Maka jumlah iterasi pada lembar kerja excel kita buat sebanyak 362 sehingga expected value dari peubah acak adalah rata-rata dari total kolom :

expected project cost =AVERAGE(H14:H375) = 73785,44

Nilai estimasi total biaya proyek didapatkan sebesar 73785,44$. Karena berdistribusi normal, letak median seharusnya sangat dekat dengan mean : 

=MEDIAN(H14:H375) = 73652,64

Perbedaanya hanya 0,18%

Informasi berguna lainnya adalah kurtosis dan skewness. Kurtosis adalah derajat keruncingan suatu distribusi (diukur relatif terhadap distribusi normal). Distribusi normal sempurna memiliki kurtosis 0.

=KURT(H14:H375) = -0,69

Nilai kurtosis yang lebih kecil dari nol mengindikasikan bahwa distribusi random variabel lebih flat dibandingkan dsitribusi normal.

Skewness atau disebut juga ukuran kemiringan adalah suatu bilangan yang menunjukan miring atau tidaknya bentuk kurva suatu distribusi . Distribusi normal sempurna memiliki skewness 0.

=SKEW(H14:H375) = -0,01

Nilai skewness yang lebih kecil dari nol tersebut di atas mengindikasikan bahwa ekor distribusi menceng sedikit ke kiri. 

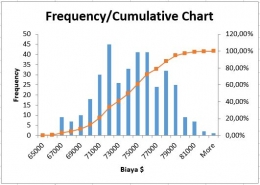
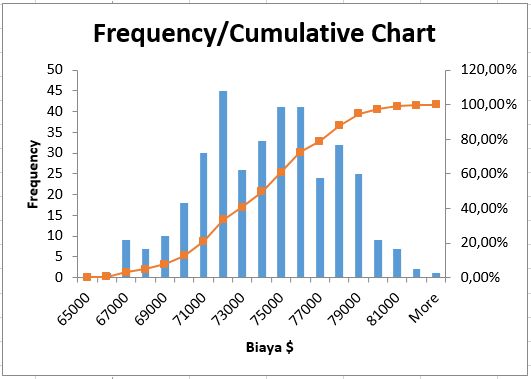
Hasil dari simulasi Monte Carlo jika diplot akan menghasilkan chart sebagaimana berikut.

DOK.ISTIMEWA

Bagi yang ingin mendownload lembar kerja saya, bisa akses di sini. :)