Frekuensi Not Tangga Nada Merupakan Deret Ukur

Bunyi dihasilkan oleh getaran.

Getaran adalah gerak bolak balik suatu benda.

Keras lembutnya bunyi ditentukan oleh besar kecilnya amplitudo getaran. Amplitudo adalah jarak simpangan terjauh dari getaran. Makin besar amplitudo makin keras bunyi.

Tinggi rendahnya suatu bunyi ditentukan oleh frekuensi getaran tersebut. Makin besar frekuensi makin tinggi bunyi. Satuan frekuensi adalah Hz (Hertz) yang artinya per detik.

Nada adalah bunyi dengan frekuensi tertentu. Deretan nada nada  tersebut dalam urutan teratur disebut tangga nada. Ada beberapa standard dan notasi tangga yang dipergunakan dan dipakai, dan dalam pembahasan ini kita memakai nada (not) balok yang identitas setiap nada ditulis dengan huruf sbb. :

C  -  D  -  E  -  F  -  G  -  A  -  B  -  C'

Nada di atas diurutkan sesuai dengan tinggi nada, yaitu urutan frekuensi nada tersebut. Nada C lebih rendah dari nada berikutnya D, yang berarti frekuensi nada C lebih kecil dari frekuensi nada D.

Diantara nada yang berurutan (kecuali E ke F, dan B ke C') masih ada nada lain dengan frekuensi berada diantara nada yang mengapitnya. Secara lengkap tangga nada tersebut dapat dituliskan sbb:

C  -  C#  -  D  -  D#  -  E  -  F   - F#  -  G  -  G#  -  A  -  A#  -  B   - C'

Tanda # (dibaca kres) berarti frekuensi naik 1/2 laras. Ada tanda lain yang lazim dipakai juga yaitu tanda b (dibaca mol), yang berarti turun 1/2 laras . Sehingga C# bisa juga ditulis Db. Demikian juga berlaku untuk nada nada lainnya.

Ada hal menarik tentang besarnya frekuensi tangga nada ini secara matematis, yaitu frekuensi nada yang berurutan membentuk deret ukur. Hal ini berarti perbandingan (rasio) frekuensi dua nada yang berurut adalah bilangan konstan. Jika frekuensi F(C) berarti frekuensi nada C, F(C#) berarti frekuensi nada C#, dan seterusnya, maka :

F(C#) / F(C) = F(D) / F(C#) = bilangan konstan = R (ratio nada)

Berapakah besarnya rasio (R) itu ?

Kita dapat menghitung R dengan matematika yang sederhana sbb. :

Frekuensi C' 2 (dua) kali frekuensi C , rentang frekuensi dari suatu frekuensi ke dua kali frekuensinya  disebut 1 oktav. 

Ada 12 nada setelah C untuk mencapai C' yang frekuensinya menjadi 2 kali, sehingga kita dapat hubungan matematis  sbb. :

R pangkat 12  = 2  sehingga R = 1.059463

Jika diketahui frekuensi salah satu nada saja maka kita akan mengetahui frekuensi dari nada nada lainnya. 

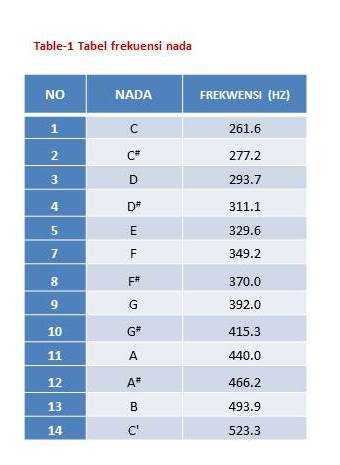
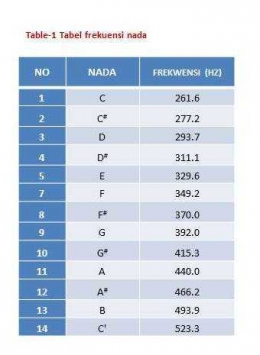
Secara internasional telah diketahui frekuensi nada A adalah 440,0 Hz. Melalui perhitungan hubungan rasio ini maka frekwensi nada lainnya dapat dihitung seperti  table pada gambar..

Frekuensi nada nada yang membentuk jutaan lagu ini tak dinyana memenuhi  hubungan matematik yang sederhana, yaitu deret ukur atau deret geometri.Hubungan matematik dalam frekuensi tangga nada ini telah penulis terapkan untuk membuat perangkat musik bell elektronik, menggunakan mikrokontroler. Salam sains.