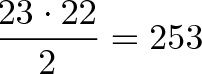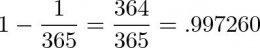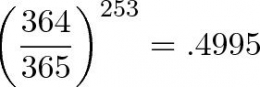Fenomena "Birthday Paradox" di Kompasianival 2020 yang Juga Ada di Sekitar Kita

Kompasianer pertama (yang terlama) adalah Katedraradjawen yang mendaftar pada tanggal 22.10.2009. Ia memiliki kesempatan 99,726027397% tanggal registrasi yang tidak sama dengan ke-19 nominator lainnya yang belum mendaftar. 99,726027397% didapatkan dari 364/365. 364 adalah jumlah hari kosong dan 365 adalah total hari dalam setahun.  

Kompasianer kedua terlama adalah Dewi Puspasari dengan tanggal 28.04.2010, memiliki rasio dengan tanggal registrasi yang sama sebanyak 363/365 =99,45%. Kompasianer ketiga terlama adalah Agung Webe memiliki rasio 362/365 =99,17%, dan Hennie Triana sebagai Kompasianer ke empat terlama memiliki rasio 361/365 =98,90%.

Perhitungan ini terus berlanjut, hingga ke Kompasianer ke-20 yang mendaftar, yaitu Rudy Gunawan pada tanggal 01.12.2019. Rudy di sini memiliki rasio kesempatan tanggal registrasi yang tidak sama dengan nominator lainnya sebanyak 345/365 =94,52%.

Birthday paradox menjelaskan bahwa angka 23 adalah kesempatan terbaik untuk mendapatkan 50% orang dengan tanggal ulangtahun yang sama. Katakanlah secara acak kita mengambil tiga Kompasianer lainnya, yaitu Anis Hidayanti, Budi Susilo, dan Widz Stoops. Dengan demikian, maka Widz Stoops akan mendapatkan rasio kesempatan sebesar 343/354 =96,89%, karena sudah ada 22 hari yang telah diambil oleh Kompasianer pertama hingga yang ke dua puluh dua.

Sekarang mari kita membalik perhitungan rasio ini dengan menggunakan pendekatan yang berbeda. Obyek perhitungan kita sudah beralih kepada probabilitas dari total 23 Kompasianer untuk memiliki dua kemungkinan saja, yaitu tanggal registrasi yang sama atau tidak sama.

Rumus matematika sederhananya sebagai berikut;

Sumber: betterexplained.com

Total 23 orang akan memiliki 253 perbandingan atau 253 probabilitas dari dua kemungkinan tanggal yang penulis jelaskan di atas.

Setiap individu memiliki kesempatan untuk tanggal registrasi yang tidak sama dengan orang kedua sebesar;

Sumber: betterexplained.com

Bagaimana dengan probabiitas dari 23 orang? Dengan menggunakan pola eksponensial, rumus yang didapatkan adalah sebagai berikut;

Sumber: betterexplained.com

Satu perbandingan menghasilkan 99,72% kemungkinan tanggal registrasi yang tidak sama, namun 253 kemungkinan hanya menyisakan 49,95%, atau 50,05% kemungkinan tanggal registrasi yang sama.

Bagi yang senang dengan itung-itungan, rumus matematika eksponensial ini cukup mengagumkan. Namun bagi yang lebih sering bingung sendiri, cukuplah dengan angka-angka yang jelimet ini.

Apa yang bisa dimaknai dari fenomena Birthday Paradoks ini?

Kesempatan Tidak Bekerja dengan Rumus Sederhana.