Soal:
Berikut ini adalah kasus pada PT, XYZ yang memperlihatkan adanya kemungkian rekonsilasi atau hubungan antara metode akuntansi keuangan komersial (x) dengan metode akuntansi perpajakan atau akuntansi fiskal (y):
2x + 3y = 13
dan 2x – 4y + 8 = 0
A. Hitunglah Nilai x, dan y pada persamaan tersebut!
B. Berapa selisih rekonsiliasi fiskal dengan metode akuntansi?
C. Buatlah jurnal pada rekonsiliasi fiscal dan komersial ini!
Jawaban:
A. Menyelesaikan Sistem Persamaan
Pertama, kita sederhanakan Persamaan 2:
2𝑥 − 4𝑦 + 8 = 0
2x − 4y = −8
Sekarang kita punya dua persamaan:
2𝑥 + 3𝑦 = 13 (Persamaan 1)
2𝑥 − 4𝑦 = −8 (Persamaan 2’)
Untuk mengeliminasi x, kita kurangkan Persamaan 2' dari Persamaan 1:
(2𝑥 + 3𝑦) − (2𝑥 − 4𝑦) = 13 − (−8)
2𝑥 + 3𝑦 − 2𝑥 + 4𝑦 = 13 + 8
7𝑦 = 21
𝑦 = 3
Sekarang kita substitusi nilai 𝑦 = 3 ke salah satu persamaan, misalnya Persamaan 1:
2𝑥 + 3𝑦 = 13
2𝑥 + 3(3) = 13
2𝑥 + 9 = 13
2𝑥 = 4
𝑥 = 2
Jadi, nilai 𝑥 dan 𝑦 adalah:
𝑥 = 2
𝑦 = 3
B. Menghitung Selisih Rekonsiliasi Fiskal dengan Metode Akuntansi
Selisih rekonsiliasi fiskal dan metode akuntansi adalah perbedaan antara nilai x dan 𝑦. Dalam konteks ini, nilai x adalah hasil dari metode akuntansi komersial dan nilai 𝑦 adalah hasil dari metode akuntansi perpajakan.
Selisih rekonsiliasi fiskal:
𝑥 − 𝑦 = 2 − 3 = −1
C. Membuat Jurnal Rekonsiliasi Fiskal dan Komersial
Berikut adalah contoh jurnal yang mencerminkan rekonsiliasi antara akuntansi komersial dan akuntansi perpajakan berdasarkan perbedaan nilai x dan y:
Jurnal untuk Akuntansi Komersial (Nilai x)
Debet: Pendapatan Rp 2.000
Kredit: Kas Rp 2.000
Jurnal untuk Akuntansi Perpajakan (Nilai y)
Debet: Pendapatan Rp 3.000
Kredit: Kas Rp 3.000
Jurnal untuk Rekonsiliasi
Untuk mencerminkan selisih rekonsiliasi fiskal, kita buat jurnal sebagai berikut:
Debet: Pendapatan (selisih) Rp 1.000
Kredit: Beban Pajak (selisih) Rp 1.000
Dengan jurnal di atas, kita mencerminkan bahwa ada perbedaan antara pendapatan yang diakui secara komersial dengan pendapatan yang diakui untuk tujuan perpajakan, yaitu selisih sebesar Rp 1.000.

Soal:
Berikut ini adalah persamaan matematika untuk utang pajak PT Dian Harapan:
ab+c = 2020
a+bc = 2021
Dimana a adalah utang pajak Divident, b Utang Pajak Bunga, dan c utang pajak royalty
Hitunglah berapa jumlah utang pajak pada persamaan tersebut!
Buatlah jurnal yang diperlukan!
Jawaban:
Langkah 1: Menyelesaikan Sistem Persamaan
Pertama, kita coba mencari hubungan antara 𝑎, 𝑏, dan 𝑐 dari kedua persamaan. Mari coba substitusi 𝑐 dari Persamaan 1 ke dalam Persamaan 2. Kita mulai dengan mengekspresikan 𝑐 dari Persamaan 1:
𝑐 = 2020 – 𝑎𝑏
Substitusi 𝑐 ke dalam Persamaan 2:
𝑎 + 𝑏 (2020 − 𝑎𝑏) = 2021
𝑎 + 2020𝑏 – 𝑎𝑏^2 = 2021
Sekarang, kita coba menyederhanakan persamaan ini:
𝑎 + 2020𝑏 – 𝑎𝑏^2 = 2021
Untuk mencari solusi yang mungkin, kita coba beberapa nilai 𝑏 dan memeriksa apakah nilai 𝑎 dan 𝑐 memenuhi kedua persamaan.
Langkah 2: Mencoba Nilai untuk Menemukan Solusi
Kita mulai dengan asumsi bahwa 𝑏 adalah bilangan bulat positif kecil. Mari kita coba 𝑏 = 1:
Jika 𝑏 = 1:
𝑐 = 2020 − 𝑎 x 1 = 2020 − 𝑎
Substitusi ini ke dalam Persamaan 2:
𝑎 + 1 (2020 − 𝑎) = 2021
𝑎 + 2020 – 𝑎 = 2021
2020 = 2021 (tidak mungkin)
Karena 𝑏 = 1 tidak memberikan solusi yang benar, kita coba 𝑏 = 2:
Jika 𝑏 = 2:
𝑐 = 2020 – 𝑎 x 2 = 2020 − 2𝑎
Substitusi ini ke dalam Persamaan 2:
𝑎 + 2 (2020 − 2𝑎) = 2021
𝑎 + 4040 − 4𝑎 = 2021
4040 − 3𝑎 = 2021
3𝑎 = 4040 – 2021
3𝑎 = 2019
𝑎 = 673
Dengan 𝑎 = 673 dan 𝑏 = 2:
𝑐 = 2020 – 2 x 673
𝑐 = 2020 −1346
𝑐 = 674
Sekarang kita periksa apakah nilai-nilai ini memenuhi kedua persamaan:
𝑎𝑏 + 𝑐 = 673 x 2 + 674 = 1346 + 674 = 2020 (benar)
𝑎 + 𝑏𝑐 = 673 + 2 x 674 = 673 + 1348 = 2021 (benar)
Langkah 3: Jumlah Utang Pajak
Jumlah utang pajak adalah jumlah dari 𝑎, 𝑏, dan c:
𝑎 + 𝑏 + 𝑐 = 673 + 2 + 674 = 1349
Langkah 4: Membuat Jurnal yang Diperlukan
Berdasarkan nilai 𝑎, 𝑏, dan 𝑐:
1.Utang Pajak Dividen (a) = Rp 673
2.Utang Pajak Bunga (b) = Rp 2
3.Utang Pajak Royalti (c) = Rp 674
Berikut adalah jurnal yang diperlukan untuk mencatat utang pajak ini:
Jurnal untuk Utang Pajak
- Debet: Beban Pajak Rp 1349
- Kredit: Utang Pajak Dividen Rp 673
- Kredit: Utang Pajak Bunga Rp 2
- Kredit: Utang Pajak Royalti Rp 674
Dengan jurnal di atas, kita mencerminkan total beban pajak yang harus dibayar serta pembagian ke dalam masing-masing jenis utang pajak yang terkait.

Langkah 1: Menentukan Fungsi Dekomposisi Penyusutan Aktiva/Depresiasi (DP)
Kita diberikan fungsi penyusutan aktiva/depresiasi (DP) sebagai berikut:
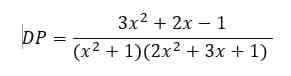
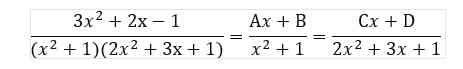
Langkah pertama adalah menggabungkan pecahan parsial ke dalam satu pecahan dengan penyebut yang sama:
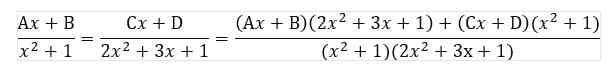
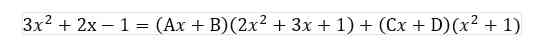
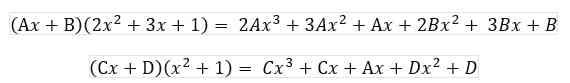
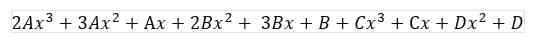
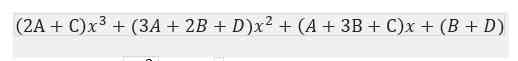
2𝐴 +𝐶 = 0 (Persamaan 1)
3𝐴 + 2𝐵 + 𝐷 = 3 (Persamaan 2)
𝐴 + 3𝐵 + 𝐶 = 2 (Persamaan 3)
𝐵 + 𝐷 = −1 (Persamaan 4)
Langkah 3: Menyelesaikan Sistem Persamaan untuk Menentukan A, B, C, dan D
Pertama, dari Persamaan 1, kita dapatkan:
𝐶 = −2𝐴
Substitusi 𝐶 ini ke dalam Persamaan 3:
𝐴 + 3𝐵 − 2𝐴 = 2
−𝐴 + 3𝐵 = 2 (Persamaan 3’)
Sekarang kita punya dua persamaan:
−𝐴 + 3𝐵 = 2 (Persamaan 3’)
𝐵 + 𝐷 = −1 (Persamaan 4)
Dan Persamaan 2:
3𝐴 + 2𝐵 + 𝐷 = 3
Dari Persamaan 4, kita dapatkan:
𝐷 = −1 – 𝐵
Substitusi 𝐷 ini ke dalam Persamaan 2:
3𝐴 + 2𝐵 − 1 − 𝐵 = 3
3𝐴 + 𝐵 – 1 = 3
3𝐴 + 𝐵 = 4 (Persamaan 2’)
Sekarang kita punya dua persamaan dengan dua variabel 𝐴 dan B:
3𝐴 + 𝐵 = 4 (Persamaan 2’)
−𝐴 + 3𝐵 = 2 (Persamaan 3’)
Kita bisa menyelesaikan sistem ini dengan metode eliminasi atau substitusi. Mari kita gunakan eliminasi. Kita kalikan Persamaan 2' dengan 3:
9𝐴 + 3𝐵 = 12 (Persamaan 2”)
Sekarang, kita tambahkan Persamaan 3' dan Persamaan 2''):
9𝐴 + 3𝐵 – 𝐴 + 3𝐵 = 12 + 2
8𝐴 + 6𝐵 = 14
4𝐴 + 3𝐵 = 7 (Persamaan 5)
Dari Persamaan 3':
−𝐴 + 3𝐵 = 2
Kita kalikan Persamaan 3' dengan 4:
−4𝐴 + 12𝐵 = 8
Menambahkan Persamaan 5 dan ini:
4𝐴 + 3𝐵 − 4𝐴 + 12𝐵 = 7 + 8
15𝐵 = 15
𝐵 = 1
Substitusi 𝐵 kembali ke dalam Persamaan 2':
3𝐴 + 1 = 4
3𝐴 = 3
𝐴 = 1
Substitusi 𝐴A kembali ke dalam 𝐶 = −2𝐴
𝐶 = −2 (1) = −2
Substitusi 𝐵B kembali ke dalam 𝐷 = −1 − 𝐵:
𝐷 = −1 – 1 = −2
Jadi, koefisiennya adalah:
𝐴 = 1, 𝐵 = 1, 𝐶 = −2, 𝐷 = −2
Langkah 4: Menentukan Lima Bentuk Persamaan TP secara Matematika
Berdasarkan koefisien yang telah kita temukan, kita dapat menulis fungsi dekomposisi DP sebagai berikut:
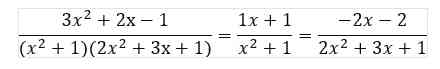
Langkah 5: Menghitung Nilai Rasional DP untuk Nilai A, B, dan C
Menggunakan nilai koefisien yang telah ditemukan 𝐴 = 1, 𝐵 = 1, 𝐶 = −2, dan 𝐷 = −2, kita substitusi ke dalam fungsi dekomposisi untuk mendapatkan nilai rasional DP:
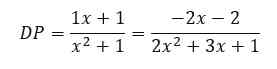
Kita dapat menghitung DP untuk nilai 𝑥 yang berbeda untuk melihat bagaimana penyusutan berubah seiring waktu atau untuk nilai-nilai tertentu yang relevan dengan skenario tertentu.
Baca konten-konten menarik Kompasiana langsung dari smartphone kamu. Follow channel WhatsApp Kompasiana sekarang di sini: https://whatsapp.com/channel/0029VaYjYaL4Spk7WflFYJ2H



















