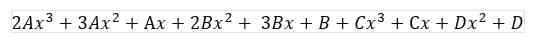Sekarang kita punya dua persamaan:
−𝐴 + 3𝐵 = 2 (Persamaan 3’)
𝐵 + 𝐷 = −1 (Persamaan 4)
Dan Persamaan 2:
3𝐴 + 2𝐵 + 𝐷 = 3
Dari Persamaan 4, kita dapatkan:
𝐷 = −1 – 𝐵
Substitusi 𝐷 ini ke dalam Persamaan 2:
3𝐴 + 2𝐵 − 1 − 𝐵 = 3
3𝐴 + 𝐵 – 1 = 3
3𝐴 + 𝐵 = 4 (Persamaan 2’)
Sekarang kita punya dua persamaan dengan dua variabel 𝐴 dan B:
3𝐴 + 𝐵 = 4 (Persamaan 2’)
−𝐴 + 3𝐵 = 2 (Persamaan 3’)
Kita bisa menyelesaikan sistem ini dengan metode eliminasi atau substitusi. Mari kita gunakan eliminasi. Kita kalikan Persamaan 2' dengan 3:
9𝐴 + 3𝐵 = 12 (Persamaan 2”)
Sekarang, kita tambahkan Persamaan 3' dan Persamaan 2''):
9𝐴 + 3𝐵 – 𝐴 + 3𝐵 = 12 + 2
8𝐴 + 6𝐵 = 14
4𝐴 + 3𝐵 = 7 (Persamaan 5)
Dari Persamaan 3':
−𝐴 + 3𝐵 = 2
Kita kalikan Persamaan 3' dengan 4:
−4𝐴 + 12𝐵 = 8
Menambahkan Persamaan 5 dan ini:
4𝐴 + 3𝐵 − 4𝐴 + 12𝐵 = 7 + 8
15𝐵 = 15
𝐵 = 1
Substitusi 𝐵 kembali ke dalam Persamaan 2':
3𝐴 + 1 = 4
3𝐴 = 3
𝐴 = 1