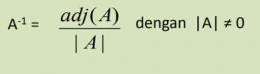Memahami 7 Jenis Matriks dan Rumus Invers Matriks Beserta Contoh Soalnya!

Dalam mata pelajaran matematika, untuk menyelesaikan suatu sistem persamaan linear tiga variabel (SPLTV) bisa menggunakan metode determinan dan invers matriks.

Sebelum kita mencari invers dari suatu matriks, maka ditentukan determinannya terlebih dahulu. Determinan adalah nilai yang bisa dihitung dari unsur-unsur suatu metrics persegi.

Invers sendiri bisa diartikan sebagai lawan dari sesuatu atau kebalikan. Apabila suatu matriks mempunyai invers, maka bisa dikatakan bahwa matriks tersebut adalah matriks nonsingular. Nah, sebaliknya, apabila suatu matriks tidak mempunyai invers, maka matriks tersebut adalah matriks singular.

Invers matriks adalah sebuah kebalikan (invers) dari kedua matriks. Jika matriks tersebut dikalikan, maka akan menghasilkan matriks persegi (AB = BA = |).

Simbol dari invers matriks adalah pangkat -1 dan letaknya berada di atas hurufnya. Sebagai sebuah contoh, matriks b adalah invers matriks A, sehingga ditulisnya dengan B = A -- 1 dan matriks A adalah invers dari matriks B ditulis dengan A = B -- 1. Matriks A dan B adalah dua matriks yang saling invers atau berkebalikan.

Adapun sifat matriks yang perlu diketahui adalah sebagai berikut:

• Suatu matriks A adalah matriks bujur sangkar.

• Apabila det (A) tidak sama dengan 0, maka matriks A mempunyai invers yaitu A-1

• Sebaliknya, apabila determinan A sama dengan 0, maka berarti A tidak memiliki invers.

Jenis-Jenis Matriks

Untuk semakin memahami invers matriks dan contoh soalnya, kamu juga bisa mengenal jenis-jenis matriks. Jenis matriks sendiri terdiri dari 8 macam, yaitu:

1. Matriks persegi

Matriks persegi, yaitu jumlah suatu elemen pada baris dan kolom yang sama. Bentuknya yang bujur sangkar membuatnya terdapat diagonal utama serta sekunder.

2. Matriks baris

Matriks baris adalah matriks dengan 1 baris hal ini yang membuat ordo dari matriks tersebut adalah A1xn

3. Matriks kolom

Matriks kolom adalah matriks yang memiliki jumlah satu kolom. Matriks yang satu ini mempunyai ordo mx1.

4. Matriks nol

Matriks nol adalah matriks dengan elemen bilangan nol dengan notasi 0 mxm.

5. Matriks identitas

Matriks identitas, adalah matriks satuan dengan semua diagonalnya memiliki nilai sama, yaitu 1. Simbolnya adalah I atau miring I.

6. Matriks skalar

Matriks skalar adalah matriks dengan elemen diagonal yang bernilai sama. A11 = a22 sampai nilai k dan dapat bernilai sembarang.

7. Matriks transpose

Matriks transpose adalah matriks yang berasal dari penukaran letak baris serta kolom matriks yang sebelumnya. Transpose sendiri disimbolkan dengan aksen T pada bagian atas matriks sebelumnya.

Rumus Invers Matriks dan Contoh Soal

Sumber: lexpress

1. Rumus Invers Matriks Berordo 2x2

Berikut ini adalah invers matriks yang digunakan untuk matriks yang memiliki ordo 2x2.

Sumber: kumparan.com

Invers matriks yang memiliki ordo 2 bisa langsung diperoleh dengan cara sebagai berikut:

• Tukar elemen-elemen pada diagonal utama.

• Berikan tanda negatif pada elemen lainya.

• Bagilah setiap elemen pada matriks dengan determinannya.

2. Rumus Invers Matriks Berordo 3x3

Mencari invers matriks yang memiliki ordo 3x3 bisa dilakukan melalui dua cara, yaitu dengan adjoin dan transformasi baris elementer.

Adjoin matriks sendiri adalah transpose dari suatu matriks yang elemen-elemennya adalah kofaktor dari elemen-elemen matriks tersebut. Maka, rumus invers matriks dengan ordo 3x3 adalah:

Sumber: kumparan.com

Dalam menentukan suatu invers matriks An dengan cara transformasi baris elementer dapat menggunakan Langkah-langkah berikut ini:

1. Bentuk matriks ini (An|In), dengan Im merupakan matriks identitas dengan ordo n.

2. Transformasikan matriks (An|In) ke dalam bentuk (In|Bn) dengan transformasi elemen baris.

3. Hasil dari langkah kedua, bisa didapat invers dari matriks An yaitu Bn.

Notasi yang paling sering digunakan dalam transformasi baris elementer di antaranya adalah sebagai berikut:

1. Bi Bj: menukarkan elemen-elemen baris ke-I dengan elemen-elemen yang ada pada baris ke-j.

2. Bi: mengalihkan tiap elemen pada baris ke-I dengan scalar k.

3. Bi + kBj: jumlahnya elemen pada baris ke-I dengan k dikalikan dengan elemen-elemen garis ke-j.

Nah, itulah rumus-rumus yang bisa kamu gunakan dalam mencari invers matriks. Kamu akan mudah mengerjakan invers matriks jika kamu sering berlatih melalui contoh-contoh soal.

Penulis: Nurul Ismi Humairoh