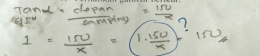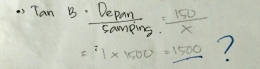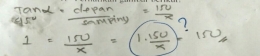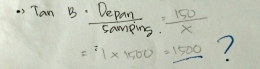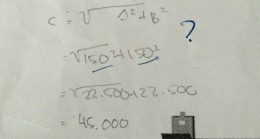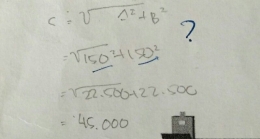ANALISIS KEMAMPUAN PENALARAN SISWA DALAM MENYELESAIAKAN SOAL PISA DITINJAU DARI KECERDASAN LOGIS MATEMATIS
Oleh: Ferry Agustian
Jurusan Tadris Matematika Fakultas Tarbiyah dan Ilmu Keguruan IAIN
Tulungagung
E-mail: ferryagustian83@gmail.com
ABSTRAK
Penalaran merupakan tujuan yang penting dalam pembelajaran matematika. Oleh karena itu, seorang guru harus mengetahui siswanya dalam menyelesaikan soal matematika. Akan tetapi masih banyak siswa yang kebingungan jika mengerjakan soal PISA. Soal PISA sangat menuntut kemampuan penalaran. Untuk itu dalam penelitian ini bertujuan untuk mendeskripsikan kemampuan penalaran siswa dalam mengerjakan soaL PISA ditinjau dari kecerdasan logis matematis. Instrumen utama dalam penelitian ini adalah peneliti. Instrumen pendukung dalam penelitian ini adalah soal PISA dan pedoman wawancara. Teknik pengumpulan datanya menggunakan tes, angket, dan wawancara. Analsisi data dilakukan dengan mereduksi data hasil tes, angket, dan wawancara kemudian disajikan dan ditarik kesimpulan.
Kata Kunci: kemampuan penalaran, soal PISA, kecerdasan logis matematis
PENDAHULUAN
Pendidikan di sekolah memiliki tujuan untuk meningkatkan daya nalar siswa terutama dalam menyelesaikan masalah mata pelajaran matematika. Penalaran merupakan aspek penting dalam pendidikan terutama pendidikan matematika. Dengan kemampuan penalaran yang baik, siswa akan memahami bahwa matematika itu bermakna. Kemampuan penalaran matematis akan menunang pemahaman matematis, mampu mengeksplor ide, mampu memperkirakan solusi, dan menerapkan ekspresi matematis dlam konteks matematika yang relevan. Terlebih lagi sesuai dengan salah satu tujuan pembelajaran matematika yang harus dicapai mengatakan bahwa kemampuan penalaran melatih cara berpikir dan bernalar dalam menarik kesimpulan, mengembangkan kemampuan pemecahan masalah, serta mengembangkan kemampuan menyampaikan informasi atau mengkomunikasikan ide-ide melalui lisan, tulisan, gambar, grafik, peta, diagam, dan sebagainya (Sumartini, 2015).
Tujuan pembelajaran matematika dan standar proses dari NCTM selaras dengan tujuan pembelajaran matematika yang dinyatakan oleh BSNP yaitu salah satunya agar siswa mempunyai kemampuan dan menggunakan penalaran pada pola dan sifat, melakukan manipulasi matematika dalam membuat generalisasi, menyusun bukti atau menjelaskan gagasan dan pernyataan matematika. baik di dalam NCTM maupun BSNP, penalaran merupakan salah satu kemampuan yang harus dicapai dalam pemebelajaran matematika (Ario, 2016). Menurut Basir penalaran matemtika bisa dijadikan sebagai fondasi dalam meahami matematika. Penalaran juga merupakan bagian integral dari pemecahan masalah. Penalaran berbeda dengan berpikir, penalaran matematika adalah bagian terpenting dalam berpikir yang melibatkan pembentukan generalisasi dan menggambarkan konklusi yang valid tentang ide dan bagaimana kaintannya antara ide-ide tersebut (Yusdiana & Hidayat, 2018). Wahyudin menyatakan bahwa kemampuan penalaran sangat penting untuk memahami matematika. Begitupun yang dikatakan Turmudi bahwasannya penalaran dan pembuuktian merupakan aspek fundamental dalam matematika. Selanjutnya Sumarno mengatakan bahwa kemampuan penalaran matematis sagat penting dalam pemahaman matematis, mengeksplor ide, memperkirakan solusi, dan menerapkan ekspresi matematis dalam konteks matematika yang relevan serta memahami bahwa matematika itu bermakna. Berdasarkan beberapa pendapat ahli di atas maka dapat disimpulkan bahwa penalaran merupakan hal yang sangat penting dalam matematika (Ario, 2016).
Namu Bentang Indria Yusdiana dan Wahyu Hidayat (Yusdiana & Hidatat, 2018) menyatakan bahwa kemampuan penalaran siswa dalam pembelajaran matematika masih rendah. Hal tersebut dikaenakan dalam proses pembelajaran masih enggunakan pembelajaran biasa sehingga siswa hanya berpusat pada guru. Pada saat pembelajaran berlangsung siswa kurang aktif, siswa hanya mendengar dan mencatat apa yang disampaikan oleh guru. Sehingga selama proses pembelajaran berlangsung kemampuan penalaran siswa masih belum terlihat. Selain itu Junaidi dan Zulkardi (Junaidi & Zulkardi, 2013) menyatakan bahwa potensi siswa dalam menggunakan penalaran dalam menjawab soal masih belum berkembang. Hal tersebut dikarenakan kurang tersedianya soal-soal yang didesain khusus yang sesuai dengan potensi dan karakter siswa.
Berdasarkan uraian di atas menunjukkan bahwasannya kemampuan penalaran matematis siswa sangat berbeda-beda. Sehingga pembelajaran matematika yang berorientasi pada kemampuan penalaran matemtatis siswa perlu diperhatikan. Banyak peneliti yang melaukukan penelitian tentang penalaran matematis diantaranya adalah (Tina Sri Sumartini, 2015; Bentang Indria Yusdiana dan Wahyu Hidayat, 2018; Marfi Ario, 2016).
Tina Sri Sumartini menyatakan bahwa penalaran merupakan ssuatu kegiatan atau proses berpikir untuk menarik kesimpulan atau membuat penyataan baru yang didasarkan pada pernyataan sebelumnya dan kebenarannya telah dibuktikan. Turmudi menyatakan bahwa kemampuan penalaran matematis merupakan suatu kebiasaan otak dikembangkan secara konsisten menggunakan berbagai macam konteks, mengenai penalaran dan pembuktian merupakan aspek-aspek fundamental dalam matematika. Dengan penalaran matematis, diharapkan siswa dapat mengajukan, menyusun bukti, dan melakukan manipulasi terhadap permasalahan matematika serta menarik kesimpulan dengan benar dan tepat (Sumartini, 2015). Jadi penalaran yang dimaksud dalam penelitian ini adalah proses berpikir dan bernalar dalam memecahkan suatu masalah kemudian diatrik sebuah kesimpulan.
Adapun indikator penalaran matematis yang diukur pada penelitian Mario Ari adalah memeriksa validitas argument, membuat analogi dan generalisasi, menarik kesimpulan logis, mengikuti turan inferensi (Ario, 2016). Indikator penalaran matematis pada penelitian Bentang Indria Yusdiana dan Wahyu Hidayat adalah melaksanakan perhitungan berdasarkan rumus/aturan matematika yang berlaku, menarik kesimpulan umum berdasarkan proses/konsep matematika yang terlihat, membuat perkiraan, dan menarik kesimpulan berdasarkan keserupaan proses/konsep matematika yang terlihat (Yusdiana & Hidayat, 2018). Adapun indikator kemampuan penalaran matematis menurut Sumarmo (2016) dalam pembelajaran matematika adalah menarik kesimpulan logis, memberikan penjelasan dengan model, fakta, sifat-sifat, dan hubuungan, memperkirakan jawaban dan proses solusi, emnggunakan pola dan hubungan utuk menganalisi situasi matematis, menyusun dan mengkaji konjektur, merumuskan lawan mengikuti aturan infereni, memeriksa validitas argumen, menyusun argumen yang valid, menyusun pembuktian langsung, tak langsung, dan menggunakan induksi matematis (Sumartini, 2015). Sedangakan indikator penalaran matematis yang digunakan dalam penelitian ini adalah melaksanakan perhitungan berdasarkan rumus/aturan matematika yang berlaku, menarik kesimpulan berdasarkan keserupaan proses/konsep matematika yang terlihat, membuat perkiraan, dan menarik kesimpulan umum berdasarkan pross/konsep matematika yang terlihat.
Pada masa ini, kualitas pendidikan sering dijadikan sebagai barometer perkembangan suatu negara, yaitu dengan mengukur kemampuan siswa dari setiap negara dalam menyelsaikan masalah matematika, sains, dan membaca serta aplikasinya dalam kehidupan sehari-hari. Terdapat dua assesmen utama beskala internasional yang menilai kemampuan matematika dan sains siwa (dalam Johar, 2012), yaitu TIMSS (Trend in International Mathematics and Science Study) dan PISA (Program for International Student Assesment). TIMSS yang disponsori oleh The International Associatio for Evaluation of Education Achievement (IEA) dilaksanakan secara regular sekali dalam empat tahun sejak 1994/1995 untuk mengetahui pencapaian siswa kelas 4 dan 8 SD dalam matematika dan sains. Fokus dari TIMSS adalah materi yang ada pada kurikulum, misalnya untuk matematika tentang bilangan, pengukuran, geometri, data dan aljabar. Sedangakan PISA yang disponsori oleh negara OECD (The Organization for Economic Cooperation ang Development) dilaksanakan secara regular sekali dalam tiga tahun sejak tahun 200 untuk mengetahui literasi siswa usia 15 tahun dalam matematika, sains, dan membaca. Fokus PISA adalah literasi yang menekankan pada keterampilan dan kompetensi siswa yang diperoleh dari sekolah dan dapat digunakan dalam kehidupan sehari-hari dalam berbagai situasi.
Indonesia beberapa kali mengikuti kedua ajang internasional di atas, namun hasilnya selalu memprihatinkan. Pada tahun 2003studi yang dilakukan oleh PISA menunjukkan prestasi Indonesia berada pada urutan 34 dari 41 negara. Pada tahun 2006, skor perolehan siswa SMP pada matematika bertengger hanya pada angka 391 (skala 0-800), padahal rata-rata skor sebesar 500. Dan berdasarkan hasil PISA terbaru 2012 pada mata pelajaran matematika (dalam Karimah & Fuad, 2017) posisi Indonesia semakin memprihatinkan yaitu berada pada urutan ke 64 dari 65 negara. Dalam studinya, PISA menguji siswa dengan tes. Wardhani (dalam Setiawan, dkk., 2014) mengemukakan bahwa soal-soal PISA sangat menuntut kemampuan penalaran dan pemecahan masalah. Sehingga hasil PISA terbaru tersebut menegaskan bahwa siswa di Indonesia masih lemah dalam kemampuan penalaran dan pemecahan masalah matematika.
Dalam meningkatkan kema,puan matematis siswa ada beberapa aspek yang harus diperhatikan, salah satunya yaitu faktor dari diri siswa. Setiap siswa mempunyai kecerdasan yang berbeda-beda sehingga berpengaruh pula pada proses penalarannya. Misalnya saja ada satu siswa yang kurang mampu dalam pelajaran matematika damun dia sangart pandai dalam olahraga. Hal tersebut sesuai dengan teori kecerdasan majemuk (multiplt intelegences). Howard Gadner, seorang psikolog ternama menyebutkan terdapat tujuh kecerdasan majemuk. Namun, pada perkembangannya, Gadner membagi kecerdasan majemuk tersebut menjadi sembilan tipe, yaitu kecerdasan linguistik, intrapersonal, matematik-logis, spasial, musikal, kinestetik, naturalis, dan eksistensial (Sholikhah, Budiyono, & Saputro, 2014). Kecerdasan logis matematis merupakan kecerdasan yang dapat dikembangkan menggunakan semua mata pelajaran. Aktivitas dalam mengembangkan kecerdasan logis matematis sangatlah luas tidak terbatas pada mata pelajaran matematika saja. Kecerdasan logis matematis menurut Yaumi adalah kemampuan yang berkenaan dengan rangkaian alasan, mengenal pola-pola dan aturan. Kemampuan ini sering disebut berpikir kritis. Kecerdasan ini berhubungan dengan kemampuan ilmiah. Oleh sebab itu dapat dikatakan bahwa kecerdasan logis matematis adalah kemampuan ilmiah untuk memahami suatu konsep dan secara prosedural menghubuungkan pola-pola abstrak dalam memcahkan suatu masalah. Kecerdasan logis matematis melibatkan banyak komponen, yaitu perhitungan matematika, logika berpikir, pemecahan masalah, penalaran, serta membedakan pola dan huubngan (Zulfairanatama & Hadi, 2013).
Penelitian tentang penalaran matematis sudah banyak dilakukan akan tetapi belum ada yang meneliti tentang kemampuan penalaran siswa dalam mengerjakan soal PISA ditinjau dari kecerdasan logis matematis. Seperti Tina Sri Sumartini meneliti tentang peningkatan kemampuan penalaran matematis melalui pembelajaran berbasis masalah. Bentang Indira Yusdiana dan Wahyu Hidayat meneliti tentang analsis kemampuan penalaran matematis siswa SMA pada materi limit fungsi. Selanjutnya Marfi Ario meneliti tentang analisis kemampaun penalaran matematis siswa SMK setelah mengikuti pemebelajaran berbasis masalah. Untuk itu perlu dilakukan sebuah penelitian mengenai kemampuan penalaran siswa dalam mengerjakan soal PISA ditinjau dari kecerdasan logis matematis. Dengan melakukan penelitian tersebt diharapkan guru dapat merancang suatu strategi maupun pembelajaran ang dapat mengoptimalkan dan meningkatkan kemampuan penalaran matematis siswa.
METODE
Peneltian ini merupakan penelitian deskriptif dengan menggunakan pendekatan penelitian kualitatif. Subjek penelitian ini adalah siswa kelas XI MA Darul Hikmah Tawangsari Tulungagung. Jumlah subjek yang digunakan adalah 3 orang siswa perempuan. Pemilihan subjek menggunakan teknik purposive sampling. Penilaian subjek juga berdasarkan angket yang disi oleh siswa dan diidentifikasi yang memiliki kecerdasan logis matematis. Instrumen yang digunakan dalam penelitian ini adalah instrumen utama dan instrumen pendukung. Instrumen utama dalam penelitian ini adalah peneliti. Instrumen pendukung dalam penelitian ini adalah soal PISA dan pedoman wawancara. Soal yang digunakan adalah 2 soal PISA tahun 2012. Pedoman wawancara yang digunakan berdasarkan indikator penalaran matematis. Teknik pengumpulan datanya menggunakan tes, angket, dan wawancara. Validitas data yang digunakan adalah triangulasi teknik. Analisis data dilakukan dengan mereduksi hasil tes, angket, dan wawancara kemudian disajikan dan ditarik kesimpulan.
HASIL PEMBAHASAN
Hasil penelitian diperoleh dari pekerjaan siswa di MA Darul Hikmah Tawwangsari Tulungagung. Berdasarkan hasil pengambilan angket logis matematis, maka dipilih TIGA siswa sebagai subjek penelitian yang dikategorikan menjadi tinggi (S1), sedang (S2), dan rendah (S3).
Kemampuan penalaran subjek penelitian dianalsisis berdasarkan indikator penalaran yaitu: (a) Melaksanakan perhitungan berdasarkan rumus/aturan matematika yang berlaku, (b) Menarik kesimpulan berdasarkan keserupaan proses/konsep matematika yang terlihat, (c) Membuat perkiraan, (d) Menarik kesimpulan umum berdasarkan proses/konsep matematika yang terlihat.
Kemampuan melaksanakan perhitungan berdasarkan rumus/aturan matematika yang berlaku.
Dalam menyelsaikan soal siswa dalap melakukan perhitungan berdasarkan rumus/aturan matematika yang berlaku setelah siswa memahmi, mempertimbangkan, dan melihat informasi yang bernilai serta melihat kemungkinan yang sesuai untuk memecahkan permasalahannya.
Jawaban Siswa
Subjek S1
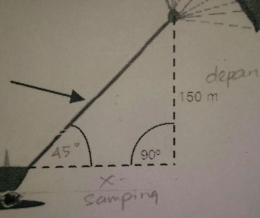
Jawaban subjek pada langkah pertama soal nomor 1 dapat dilihat pada gambar 1
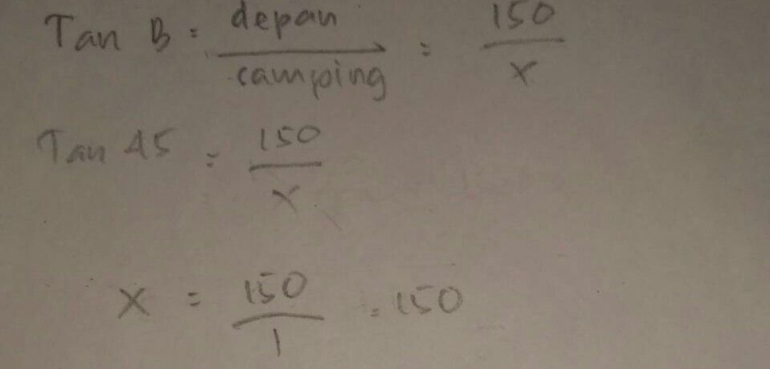
Terkait dengan indikator tersebut, berikut disajikan wawancara peneliti dengan S1.
Peneliti:"Perhatikan soal nomor 1, informasi apa saja yang dapat kamu ketahui dalam soal tersebut?"
S1: "Banyak, informasi yang saya ketahui saya tulis di gambar soal."
Peneliti:"Setelah mengetahui informasi tersebut, apa yang kamu lakukan."
S1:"Saya cermati terlebih dahulu, baru kemudian saya dapat menetukan rumus matematika yang akan saya gunakan untuk menemukan jawaban soal nomor 1."
Peneliti:"Rumus matematika apa yang kamu gunakan dalam menentukan jawaban?"
S1:"Rumus perbandingan trigonometri tan seperti jawaban saya ini Pak."
Peneliti:"x di sana mewakili apa?"
S1:"Tadi sudah saya misalkan bahwa x adalah panjang sisi samping."
Peneliti:"Bagaimana caranya x berpindah ke ruas kiri?"
S1:"Caranya dengan mengkalikan kedua ruas dengan huruf x dan kedua ruas dibagi dengan tan 45."
Peneliti:"Angka 1 itu diperoleh dari mana?"
S1:"tan 45 kan samadengan 1 Mas."
Berdasarkan hasil wawancara di atas, dapat dilihat bahwa S1 mampu melaksanakan perhitungan berdasarkan rumu/aturan matematika dengan baik. S1 asih mengingat rumus dari materi sebelumnya yang telah diajarkan. Dalam mengerjakan soal ini siswa bisa mencari informasi terlebih dahulu yang ada pada soal. Informasi tersebut digunakan siswa untuk menjawab soal. Siswa tidak merasa kesulitan dalam mengerjakan soal tersebut.
Subjek S2

Sesuai jawaban gambar 2 siswa megetahui apa saja yang diketahui (besar sudut dan tinggi) dan yang ditanyakan salam soal. Siswa mampu menetukan rumus yang dipakai namun pada proses perhitungan terdapat salah penulisan dimana siswa harusnya telah dapat menarik kesimpulan atas proses perhitungannya tetapi malah ditulis kembali model perhitungan sebelmnya.
Terkait dengan indikator tersebut, berikut disajikan hasil wawancara peneliti dengan S2.
Peneliti:"Perhatiakn soal nomor 1, informasi apa saja yang kamu ketahui dalam soal tersebut?"
S2:"Besar sudut dan tinggi segitiga."
Peneliti:"Setelah mengetahui informasi tersebut, apa yang kamu lakukan?"
S2:"Saya menentukan rumus untuk menjawab soal nomor 1."
Peneliti:"Rumus matematika apa yang kamu gunakan dalam menentukan jawaban?"
S2:"Rumus tan yaitu depan dibagi samping."
Peneliti:"x disana mewakili apa?"
S2:"x mewakili panjang sisi samping."
Peneliti:"Angka 1 itu diperoleh darimana?"
S2:"Hasil tan 45 Pak."
Peneliti:"Kenapa angka 1 tersebut dikalikan dengan 150 per x?"
S2:"Oh iya Pak, itu salah saya seharusnya menuliskan x sama dengan sehingga x diperoleh 150."
Berdasarkan wawancara di atas, S2 mampu melaksanakan perhitungan berdasarkan rumus/aturan matematika dengan cukup baik. Dalam mengerjakan soal ini siswa bisa mencari informasi terlebih dahulu yang ada pada sal. Informasi tersebut digunakan siswa untuk menjawab soal. Akan tetapi dalam menjawab soal masih terdapat proses yang salah
Subjek S3

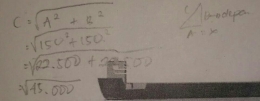
Sesuai jawaban gambar 3 siswa tidak menuliskan informasi yang ada dalam soal. Jawaban siswa tiadk terorganisi dengan baik. Hal tersebut dikarenakan siswa belum memahami soal, sehingga dalam menjawab soal siswa belum mampu melaksanakan perhitungan berdasarkan rumus/aturan matematika.
Terkait dengan indikator tersebut, berikut disajikan hasil wawancara peneliti dengan S3.
Peneliti:"Perhatikan soal nomor 1, informasi apa saja yang dapat kamu ketahui dalam soal tersebut?"
S3:"seperti yang ada dalam soal."
Peneliti:"Setelah mengetahui informasi tersebut, apa yang kamu lakukan?"
S3:"Saya langsung menjawab soalnya."
Peneliti:"Rumus matematika apa yang kamu gunakan dalam menentukan jawaban?"
S3:"Rumus yang seperti saya tulis Pak."
Peneliti:"x mewakili apa?"
S3:"tidak tau Pak."
Peneliti:"Angka 1 itu darimana?"
S3:"Tidak tau Pak, saya asal jawab. "
Berdasarkan hasil wawancara di atas, S3 belum mengetahui apa saja yang dikerjakan dalam soal. Siswa masih merasa bingung dalam menentukan rumus/aturan matematika yang digunakan dalam menjawab soal.
Kemampuan siswa dalam menarik kesimpulan berdasarkan keserupaan proses/konsep matematika yang terlihat.
Subjek S1
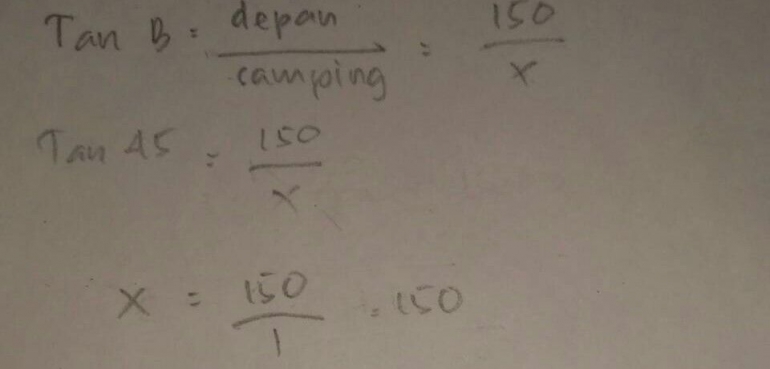
Peneliti:"Dari perhitungan yang telah kamu lakukan, apa yang kamu dapatkan atau apa yang dapat kau smpulkan?"
S1:"Saya mendapatkan panjang sisi samping dengan nilai 150."
Peneliti:"Lalu, apa yang kamu lakukan dengan nilai panjang sisi samping tersebut?"
S1:"Untuk melengkapi informasi yang dibutuhkan untuk mencari jawaban dari pertanyaan sebenarnya."
Berdasarkan wawancara di atas, S1 mampu menarik kesimpulan berdasarkan keserupaan proses/konsep matematika yang telah ia selesaikan.
Subjek S2

S2:"Untuk menjawab langkah selanjutnya Pak."
Bedasarkan wawancara di atas, S2 mampu menarik kesimpulan berdasarkan keserupaan proses/konsep matematika yang telah ia selesaikan.
Subjek S3

Peneliti:"Dari perhitungan yang telah kamu lakukan, apa yang kamu dapatkan atau apa yang dapat kamu simpulkan?"
S3:"Saya jawabnya 1500 Pak."
Peneliti:"Lalu apa yang kamu lakukan dengan nilai 1500 tersebut?"
S3:"Buat langkah berikutnya Pak."
Berdasarkan wawancara di atas, S3 masih kurang dalam menarik kesimpulan berdasarkan keserupaan proses/konsep matematika yanng telah ia selesaikan.