Pagi itu sekitar tiga puluh dua siswa kelas sembilan duduk berkeliling di aula. Empat siswa sedang memberikan penjelasan sekaligus praktik , sementara yang lain memperhatikan.
Penjelasan berkisar tentang bagaimana cara menaksir tinggi sebuah obyek.
Sebuah tongkat dipegang dalam posisi berdiri oleh seorang siswa, sementara satu siswa yang lain terlentang sambil mengintai ke arah obyek yang akan ditaksir ketinggiannya. Dalam hal ini obyeknya adalah lampu gantung di aula.

Sementara siswa yang terlentang mengintai obyek dengan teliti, siswa yang berdiri memegang tongkat menandai posisi titik di tongkat yang membentuk garis lurus antara mata, dan obyek. Tampak sekali kerjasama yang baik di antara mereka.
Hasil pengamatan lalu mereka catat dan dipakai sebagai dasar untuk menaksir ketinggian lampu gantung.
Empat siswa yang praktik di atas adalah siswa yang tergabung dalam pramuka inti sekolah.
Dalam pembelajaran matematika kali ini saya sengaja mengajak siswa pramuka berkolaborasi , karena topiknya akrab dengan dunia pramuka yaitu penerapan kesebangunan segitiga untuk memecahkan masalah di sekitar kita.
Jika di tulisan sebelumnya saya menulis tentang penggunaan klinometer untuk menghitung ketinggian obyek dengan menggunakan konsep kesebangunan segitiga, kali ini saya bercerita bahwa ternyata konsep matematika juga banyak digunakan dalam pramuka.

Kegiatan Pramuka yang menggunakan konsep matematika misalnya mengukur lebar sungai, pioneering, pendirian tenda, juga saat menaksir tinggi suatu obyek ketika mereka melakukan kegiatan di lapangan.
Sesuai tema pembelajaran kali ini yang dibahas adalah bagaimana pramuka menaksir ketinggian obyek dengan menggunakan konsep kesebangunan segitiga.
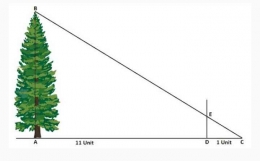
Menaksir tinggi obyek adalah salah satu ketrampilan Pramuka yang tercantum dalam SKU (Syarat Kecakapan Umum) pramuka. penggalang. Nah, bagaimana langkah-langkahnya? Mari kita simak bersama: ( Obyek yang dipakai adalah pohon)

1. Ambil posisi di depan pohon yang akan ditaksir ketinggiannya kira-kira 11 satuan panjang. Satuan panjang bisa menggunakan tongkat atau langkah kaki dari titik A ke Titik D.
2. Letakkan tongkat pada titik D dalam posisi berdiri (dipegang oleh salah satu anggota pramuka).
3. Hitung satu satuan panjang lagi dan beri nama dengan titik C.
4. Dari Titik C, seorang anggota pramuka diminta untuk mengintai ke puncak pohon (B) melalui tongkat yang ditegakkan pada Titik D.

5. Tandai bagian tongkat yang dilalui garis CB. Dan titik pertemuan tersebut diberi nama Titik E.
Rumus untuk mencari Tinggi pohon adalah AB = 12 x DE
Ternyata dibagian akhir inilah konsep kesebangunan segitiga muncul.
Dalam gambar di atas ada dua segitiga yang sebangun yaitu ABC dan DEC. Karena sebangun maka berlaku perbandingan :
AB/DE = AC/DC = BC/EC
Dari perbandingan tersebut diambil perbandingan AB/DE = AC/DC, dan diperoleh
1/12 = DE / AB atau
AB = 12 x DE,
Karena AB adalah tinggi pohon, maka
tinggi pohon = 12 x DE.
Misal:
Jika diperoleh DE= 50 cm, maka tinggi pohon adalah 12 x 50 cm = 600 cm atau 6 meter.
Mudah sekali bukan?
Siswa pagi itu demikian antusias dalam mengikuti pembelajaran. Siswa yang berperan sebagai narasumber memberikan penjelasan langkah-langkah secara detail, sementara siswa yang lain memperhatikan dengan seksama.

Sesekali mereka mencatat bagian-bagian penting dari penjelasan yang ada, sementara guru memberikan penguatan yang diperlukan pada penjelasan siswa.
Meski yang menjadi 'guru' saat itu adalah teman siswa sendiri, semua tetap serius mengikuti pembelajaran karena ada tugas akhir berupa laporan yang harus dikumpulkan.
Ya, penjelasan yang diberikan oleh pramuka pagi itu demikian menarik.
Ilmu yang baru bagi siswa yang lain.
Beberapa pertanyaan dilontarkan siswa pada 'guru' mereka, seperti mengapa harus terlentang atau bagaimana cara mengukur jarak dari pengamat ke obyek jika tidak membawa meteran. Dan semua pertanyaan dijawab dengan jelas sesuai dengan apa yang sering dipraktekkan pramuka di lapangan.

Aha, pembelajaran yang sangat menyenangkan. Dengan kolaborasi antara pramuka dan matematika hari itu siswa bisa belajar bagaimana menerapkan konsep matematika untuk memecahkan masalah- masalah yang ada di sekitar kita.
Satu hal lagi yang tak kalah penting adalah menunjukkan pada siswa bahwa matematika bukan sekedar kumpulan rumus atau materi yang sulit. Hakekatnya matematika sangat dekat dengan kehidupan kita sehari-hari.
Semoga bermanfaat dan salam matematika
Sumber bacaan : http://panduan-kepramukaan.blogspot.com/2016/12/cara-menaksir-tinggi-metode-i.html
Baca konten-konten menarik Kompasiana langsung dari smartphone kamu. Follow channel WhatsApp Kompasiana sekarang di sini: https://whatsapp.com/channel/0029VaYjYaL4Spk7WflFYJ2H