Apakah materi matematika yang paling sulit di kelas 8? Jika ditanyakan pada siswa jawabannya biasanya hampir sama yaitu Persamaan Garis Lurus (PGL).Dalam proses pembelajaran materi PGL selalu memakan waktu yang lebih banyak dibanding materi yang lain. Jika materi yang lain bisa dihabiskan dalam waktu kira-kira 2-3 minggu, PGL bisa 4-5 minggu. Mengapa? Banyak rumus yang harus dihafal dan kadang bingung harus menggunakan rumus yang mana.
Tentang Materi Persamaan Garis Lurus
Garis hakekatnya adalah kumpulan titik-titik yang yang banyaknya tak terhingga dan posisinya saling berdampingan.
Persamaan Garis Lurus bisa dinyatakan dengan y= mx + c atau ax +by + c = 0
Ada banyak manfaat dari belajar materi PGL ini di antaranya adalah untuk menentukan nilai kemiringan suatu bangunan, menentukan hubungan antara jarak, waktu dan kecepatan, dan meramalkan harga suatu barang dalam kurun waktu tertentu.
Ada tiga rumus yang dipakai dalam pembelajaran PGL yaitu:

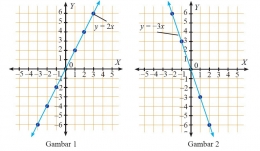
Untuk menentukan gradient sebuah garis cukup mengambil koordinat dua titik sembarang, lalu kita masukkan ke dalam rumus pertama.
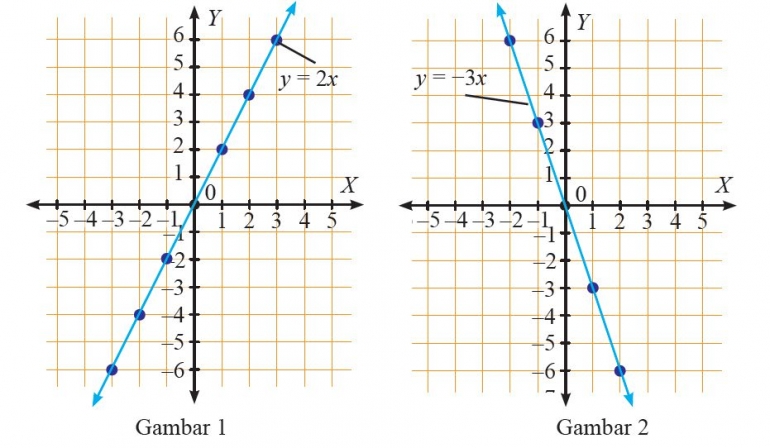
Dengan cara yang sama, untuk menentukan gradient garis pada gambar kedua kita ambil titik (-1,3) dan (-2,6), dan diperoleh gradiennya adalah 6-3 / -2-(-1)= -3
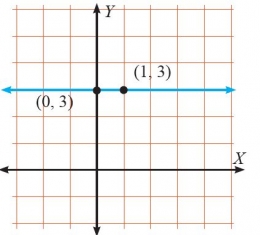
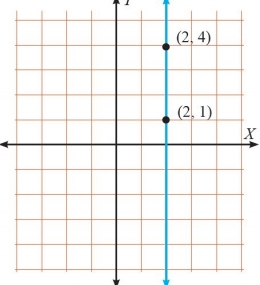
Bagaimana dengan garis yang sejajar dengan sumbu x dan sumbu y?
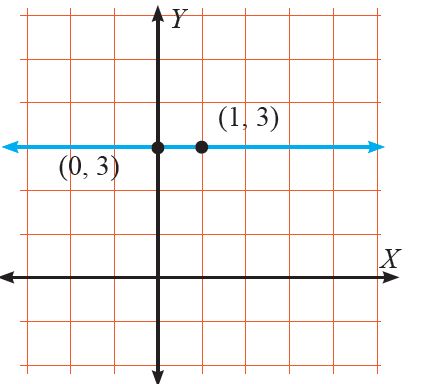
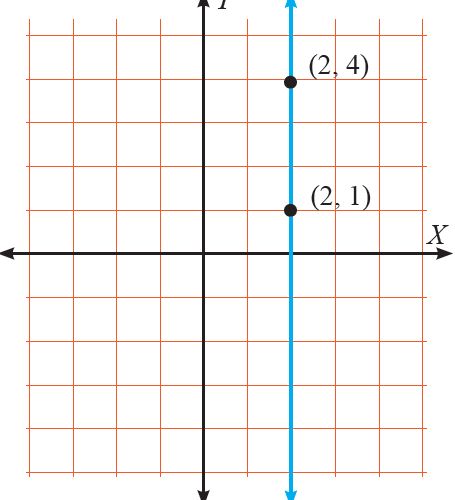
Dapat diambil kesimpulan bahwa berdasarkan gradiennya ada bermacam-macam posisi garis lurus:
1. Jika gradiennya negatif, garis miring ke kiri .
2. Jika gradiennya positif, garis miring ke kanan
3. Jika gradiennya nol ,posisi garis sejajar sumbu x (horizontal) dan
4. Garis yang sejajar sumbu y (vertikal) tidak punya gradien
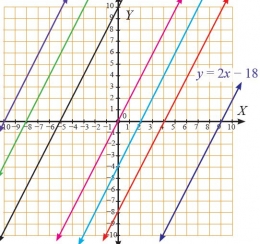
Karena gradient menunjukkan kemiringan garis, garis yang mempunyai gradien sama akan sejajar. Sebaliknya jika gradiennya tidak sama,maka mereka pasti akan saling berpotongan.
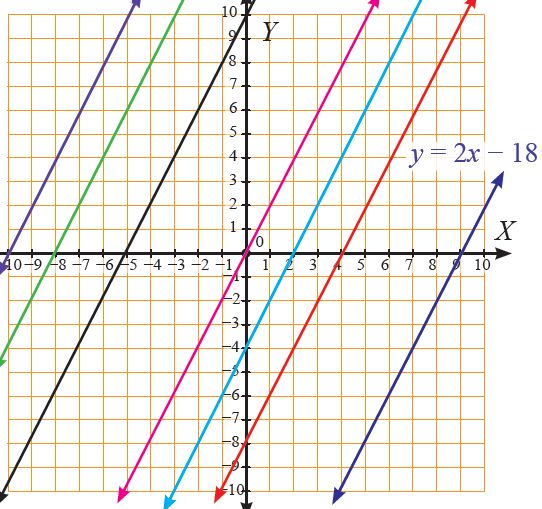

Semoga bermanfaat dan salam matematika... :)
Baca konten-konten menarik Kompasiana langsung dari smartphone kamu. Follow channel WhatsApp Kompasiana sekarang di sini: https://whatsapp.com/channel/0029VaYjYaL4Spk7WflFYJ2H