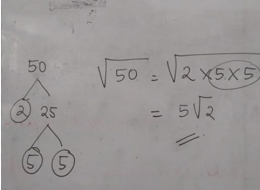Pagi itu kelas saya mulai pembahasan tentang operasi bentuk akar. Operasi bentuk akar adalah sub materi Bilangan Berpangkat dan Bentuk Akar yang dipelajari di kelas 9 semester gasal.
Untuk mengecek pemahaman siswa tentang bentuk akar saya mulai dengan memberikan pertanyaan-pertanyaan sederhana.
"Berapakah akar dari 16?"
"Empat!" jawab siswa cepat.
"Pintar, akar 100?" lanjut saya.
"Sepuluh," jawab siswa yang lain lagi. Suasana semakin hangat. Ada empat atau lima contoh lagi yang saya tanyakan dan siswa selalu menjawab dengan antusias. Namun saat pertanyaan terakhir tiba-tiba jawaban macet. Tidak ada seorangpun yang angkat tangan.
"Akar 50?" tanya saya.
Kelas langsung diam. Siswa saling menoleh.
"Tidak ada, Bu," kata Achmad.
"Ada, Achmad," jawab saya sambil tersenyum. Achmad pasti beranggapan bahwa hasilnya harus bilangan bulat.
"Boleh pakai kalkulator, Bu?" tanya seorang siswa.
"Tidak boleh," jawab saya. Mengapa tidak boleh? Cara mencari akar sudah pernah dipelajari siswa dikelas 8. Ketika mereka mempelajari teorema Pythagoras.
Seorang siswa tiba-tiba angkat tangan dan menjawab. Sebutlah namanya Della.
"Lima akar dua, Bu," jawab Della yakin..
"Wow, pintar sekali," komentar saya antusias.
"Della bisa menerangkan dari mana diperoleh lima akar dua?" tanya saya pada Della.
Dengan sigap Della maju dan menuliskan cara mendapatkan jawaban tersebut.
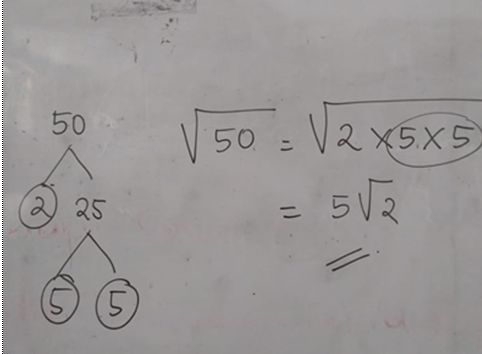
Della membuat perkalian bilangan prima yang menghasilkan 50 dengan menggunakan pohon faktor yaitu 2x5x5.
Jadi diperoleh akar 50 sama dengan akar 2 x 5 x 5. Karena akar 5 x 5 adalah 5, dan akar 2 bukan bilangan bulat, maka hasil dari akar 50 adalah 5 akar 2.
Jawaban yang benar. Siswa sekelas segera memberi applaus untuk Della.
Nah, sekarang mari kita cermati jawaban Della.
Dalam matematika akar 2 termasuk bilangan irrasional. Karena itu 5 akar 2 juga bilangan irrasional.

Apakah bilangan irrasional itu?
Sebelum membahas apakah bilangan irrasional itu mari kita pelajari bermacam-macam himpunan bilangan dalam matematika.
Dalam Matematika SMP dikenal bermacam-macam himpunan bilangan, di antaranya yaitu:
Himpunan bilangan asli ={1,2,3,4,5,6,7,...}
Himpunan bilangan cacah={0,1,2,3,4,5,6,7,...}
Himpunan bilangan bulat={...-3,-4-2,-1,0,1,2,3,4,5,...}
Selain himpunan bilangan di atas masih ada himpunan bilangan pecahan. Nah, gabungan dari himpunan bilangan bulat dan bilangan pecahan inilah yang dinamakan bilangan rasional
Ada himpunan bilangan rasional adapula himpunan bilangan irrasional. Gabungan dari keduanya membentuk himpunan bilangan real (nyata).
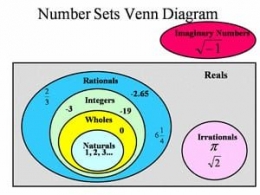
Hubungan antara berbagai himpunan bilangan tersebut dapat dinyatakan dalam diagram Venn sebagai berikut:
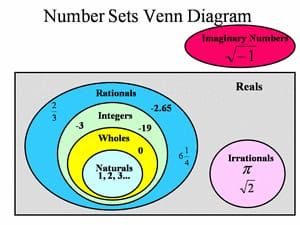
Keterangan:
Naturals: Bilangan asli
Wholes: Bilangan cacah
Integers: Bilangan bulat
Rationals: Bilangan rasional
Irrationals: Bilangan irrasional
Perbedaan Bilangan Rasional dan Irrasional
Bilangan rasional adalah bilangan yang dapat dinyatakan dalam bentuk pecahan a/b, dengan a dan b bilangan bulat.
Apa contohnya?
3 adalah bilangan rasional, karena bisa dinyatakan dalam bentuk 3/1, 6/2, 15/5 dan lainnya.
3/6 jelas bilangan rasional karena sudah dalam bentuk a/b, di mana a adalah 3 dan b adalah 6.
0,15 juga rasional karena bisa dinyatakan dalam bentuk 15/100 atau 3/20.
Dan masih banyak contoh yang lain.
Adapun ciri bilangan rasional adalah:
1. Jika dinyatakan dalam bentuk desimal maka angka di belakang koma banyaknya terbatas.
Contoh: 1/4=0.25, 2/10=0.2, atau
2.Jika angka di belakang koma banyaknya tak terbatas, pasti ada pengulangan yang teratur.
Contoh: 1/3=0.33333..., 1/9= 0.111111..., 1/6 = 0.16666... dst.
Lalu apakah bilangan irrasional itu? Sesuai namanya bilangan irrasional berarti yang bukan rasional. Yang jelas bilangan irrasional tidak bisa dinyatakan dalam bentuk a/b. dengan a dan bilangan bulat.
Ciri dari bilangan irrasional adalah jika dijadikan bilangan desimal maka angka di belakang koma tidak pernah berhenti dan tidak ada pola yang teratur. Contohnya akar 50, jika kita hitung dengan kalkulator akar 50 adalah 7,0710678119...
Tidak ada pengulangan yang teratur dan tidak pernah berhenti.
Contoh bilangan irrasional yang lain adalah pi. Dimana pi adalah 3,14159265358979323846... terus berlanjut dan tidak ada keteraturan pola di sana.
Jelas bahwa jika bilangan rasional dijadikan desimal, maka angka di belakang koma jumlahnya terbatas, atau tidak terbatas tapi menunjukkan keteraturan pola. Dan jika bilangan irrasional dijadikan desimal, maka angka di belakang koma tidak beraturan dan tidak terbatas.
Apa pelajaran yang bisa diambil?
Jika boleh dianalogikan dengan kehidupan di masyarakat, apabila kehidupan dalam masyarakat berjalan sesuai pola atau aturan yang ada, dalam arti tiap anggota masyarakat mentaaati semua peraturan, maka bisa dikatakan anggota masyarakat sudah bersikap rasional.
Namun jika tiap anggota masyarakat bertindak seenaknya sendiri, tidak ada peraturan yang tegas, dan keadaan ini dibiarkan terus menerus, maka bisa dikatakan bahwa anggota masyarakat sudah bersikap irrasional.
Dari diagram Venn di atas diketahui bahwa bilangan rasional dan irrasional membentuk bilangan nyata. Menggambarkan kenyataan bahwa dalam kehidupan kita sehari-hari, ada orang yang bisa bersikap rasional dan ada pula yang tidak.
Bagaimana menurut sahabat Kompasianer?
Salam matematika..:)
Baca konten-konten menarik Kompasiana langsung dari smartphone kamu. Follow channel WhatsApp Kompasiana sekarang di sini: https://whatsapp.com/channel/0029VaYjYaL4Spk7WflFYJ2H