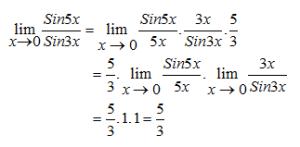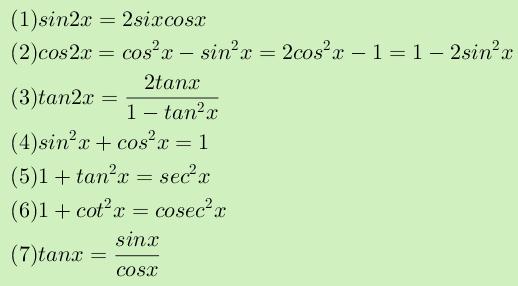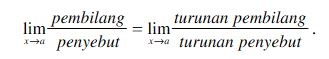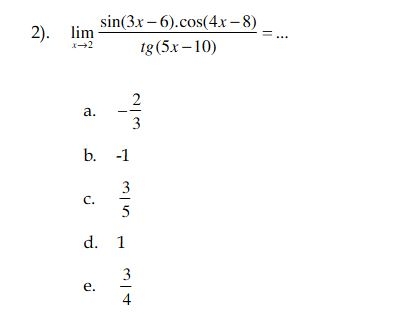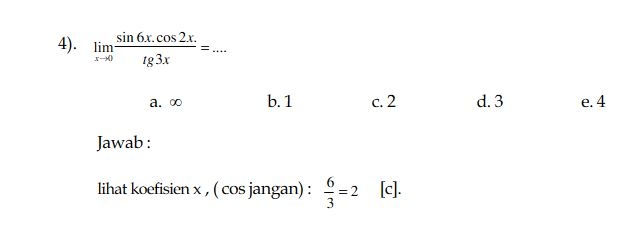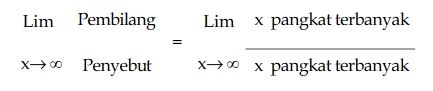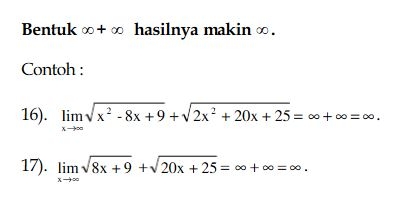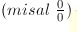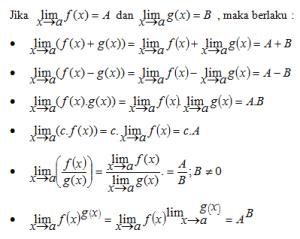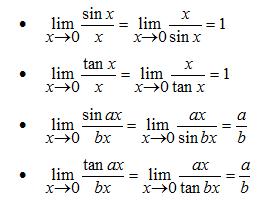Dalam menyelesaikan limit fungsi trigonometri tentunya kita harus tahu tentang fungsi trigonometri baik dari rumus, sifat, identitas dan lain sebagainya yang dapat membantu dalam menyelesaikan soal limit fungsi trigonometri. Karena dalam menyelesaikan soal limit fungsi trigonometri tidak jauh berbeda dengan penyelesaian soal trigonometri lainnya. Substitusi dahulu nilai yang didekati x ke f(x).Jika langsung didapat hasinya, maka itulah jawabannya tetapi jika menjadi bentuk
harus diselesaikan dengan cara tertentu dan kitapun harus mencari penyebabnya. Cara memfaktorkan dan mengalikan dengan sekawan masih dapat digunakan untuk menyelesaikan limit trigonometri jika didapat bentuk tak tentu. Khusus untuk limit trigonometri ada teorema untuk menyelesaikan limit dengan bentuk nol per nol. berikut ini adalah teorema limit fungsi trigonometri.

Teorema ini tidak selalu digunakan dalam menyelesaikan soal limit fungsi trigonometri, adakalanya kita mengubah bentuk trigonometri dengan menggunakan identitas trigonometri.
Berikut ini sifat-sifat limit fungsi trigonometri yang dapat digunakan dalam penyelesaian limit fungsi trigonometri.
Sifat-sifat Limit
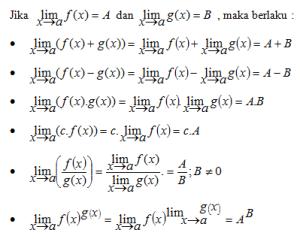
Rumus-rumus besar limit

Rumus-rumus Limit Fungsi Trigonometri
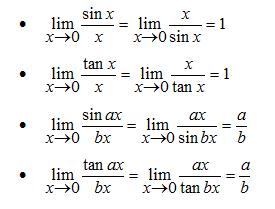
Cara menentukan Limit

Contoh saol :

Rumus-rumus identitas limit fungsi trigonometri

Trik 1 (Cara Sebenarnya )

Asalkan : kalau x diganti a , pembilang = 0 dan penyebut = 0. ( Bentuk 0/0 )
Contoh :



B. LIMIT 0/0 TRIGONOMETRI
Trik 2
Limit 0/0 trigonometri yang operasinya hanya “/”&”×”Sin dan tg ambil koefisien x nya saja
Cara ini berlaku kalau operasi antar sukunya hanya “×” dan “/” dan kalaupun ada cosharus cos yang jika dimasukan angka limitnya didapat cos 0




C. LIMIT ∞/∞
TRIK 3
Limit tak hingga hanya dipengaruhi oleh variabel (x) dengan pangkat terbanyak.



D. LIMIT ∞-∞
TRIK 4




Follow Instagram @kompasianacom juga Tiktok @kompasiana biar nggak ketinggalan event seru komunitas dan tips dapat cuan dari Kompasiana
Baca juga cerita inspiratif langsung dari smartphone kamu dengan bergabung di WhatsApp Channel Kompasiana di SINI