Jelaskan Apa Itu Modus dalam Matematika secara Lengkap dan Akurat
Dalam matematika, "modus" adalah salah satu ukuran tendensi sentral dalam statistika, yang menggambarkan nilai yang paling sering muncul dalam suatu himpunan data. Dengan kata lain, modus adalah nilai yang memiliki frekuensi kemunculan tertinggi dalam suatu kumpulan data.
Sebagai contoh, jika kita memiliki data sebagai berikut:
- 2, 4, 4, 6, 7, 4, 8
Maka, modus dari data ini adalah 4, karena angka 4 muncul lebih sering dibandingkan angka lainnya.
Jika dalam sebuah kumpulan data ada dua atau lebih nilai yang sama-sama sering muncul, maka data tersebut disebut bimodal (dua modus) atau multimodal (lebih dari dua modus). Sementara itu, jika semua nilai muncul dengan frekuensi yang sama, maka dikatakan bahwa data tersebut tidak memiliki modus.
Pengertian Modus dalam Matematika
Dalam statistika, modus dalam matematika adalah nilai yang sering muncul dari data. Ini berbeda dengan mean dan median. Modus fokus pada nilai yang dominan atau sering ditemukan.
Definisi Modus
Modus adalah nilai yang paling sering muncul dalam data. Ini penting dalam statistika deskriptif, bersama dengan mean dan median.
Perbedaan Modus dengan Mean dan Median
Ada perbedaan antara modus, mean, dan median:
- Modus adalah nilai yang sering muncul dalam data.
- Mean adalah rata-rata dari data, dihitung dengan menjumlahkan dan membagi.
- Median adalah nilai tengah dari data yang sudah diurutkan.
Modus, mean, dan median membantu analisis data. Mereka memberikan informasi tentang distribusi data.
Apa Itu Modus dalam Matematika
Modus adalah ukuran pemusatan data penting dalam matematika dan statistika. Ini adalah nilai yang muncul paling sering dalam data. Modus menunjukkan nilai yang paling populer atau dominan dalam suatu kumpulan data.
Modus berguna untuk mengidentifikasi tren atau pola dalam data. Ini berguna dalam analisis pasar, prediksi tren, dan membuat keputusan berbasis data. Modus juga memberikan informasi tentang karakteristik dasar data, terutama jika data tidak terdistribusi normal.
Dalam statistika, modus penting untuk menggambarkan nilai dominan dalam data. Ini membantu menganalisis pola dan tren dalam data. Modus berguna dalam pemasaran, ekonomi, dan ilmu sosial.
Cara Menentukan Modus dari Data Kelompok
Modus adalah nilai yang muncul paling sering dalam data. Bagaimana cara menghitung modus dari data kelompok? Ini langkah-langkahnya:
Langkah-langkah Mencari Modus Data Kelompok
- Temukan kelas dengan frekuensi paling tinggi. Ini adalah kelas modus.
- Jika ada dua kelas atau lebih dengan frekuensi sama, ada lebih dari satu modus.
- Hitung nilai tengah dari kelas modus. Ini adalah perkiraan modus.
- Untuk hasil lebih akurat, gunakan rumus modus: Modus = L + [(f1 - f0) / (2f1 - f0 - f2)] * c di mana:
- L = Batas bawah kelas modus
- f1 = Frekuensi kelas modus
- f0 = Frekuensi kelas sebelum modus
- f2 = Frekuensi kelas setelah modus
- c = Panjang kelas
Ikuti langkah-langkah ini untuk menghitung modus dari data kelompok dengan mudah. Ingat, statistika penting dalam analisis data dan memahami pola.
Menghitung Modus untuk Data Tidak Berkelompok
Kita bisa menghitung modus dari data yang tidak berkelompok. Data ini tidak disusun dalam interval atau kelas tertentu. Berikut cara menghitung modus untuk data seperti ini:
- Buat tabel distribusi frekuensi. Tabulasikan data dan catat setiap nilai beserta frekuensinya.
- Identifikasi nilai yang paling sering muncul. Nilai dengan frekuensi tertinggi adalah modus dari data.
Contoh data nilai ulangan harian matematika siswa: 80, 75, 82, 78, 75, 80, 85, 75, 78. Kita buat tabel distribusi frekuensi dulu:
Nilai 75 muncul paling sering, yaitu 3 kali. Jadi, modus dari data nilai ulangan adalah 75.
Untuk menghitung modus data tidak berkelompok, cukup sederhana. Buat tabel distribusi frekuensi dan cari nilai yang paling sering muncul. Ini membantu kita analisis pola dan tren dalam data.
Kegunaan Modus dalam Analisis Data
Modus sangat penting dalam statistik. Ini membantu kita mengerti karakteristik data. Kita bisa mendapatkan wawasan berharga dari modus.
Manfaat Modus dalam Statistik Deskriptif
Dalam statistik deskriptif, modus berguna untuk:
- Mengidentifikasi nilai yang sering muncul.
- Menggambarkan kecenderungan data.
- Menunjukkan pola dominan dalam data.
- Membantu analisis distribusi frekuensi.
Informasi ini membantu peneliti memahami struktur dan karakteristik data. Kegunaan modus dalam analisis data dan statistik deskriptif sangat penting.
Memahami modus membantu peneliti membuat keputusan yang lebih baik. Mereka bisa berdasarkan informasi dari data.
Contoh Soal dan Pembahasan Modus
Mempelajari konsep modus dalam matematika tidak hanya berhenti pada definisi dan perbedaannya dengan mean dan median. Untuk lebih memahami penerapan modus, mari kita lihat beberapa contoh soal modus beserta pembahasannya.
Dalam pembelajaran matematika dan statistika, kemampuan menghitung dan menginterpretasikan modus menjadi penting.
Contoh Umum
Berikut adalah beberapa contoh soal modus yang dapat membantu Anda memperkuat pemahaman:
- Diketahui data nilai ujian matematika siswa kelas X: 78, 82, 75, 82, 80, 82, 75. Hitunglah modus dari data tersebut.
- Dalam sebuah survei pengeluaran rumah tangga, diperoleh data sebagai berikut: Rp 2.500.000, Rp 3.000.000, Rp 2.800.000, Rp 3.200.000, Rp 2.500.000. Tentukan modus dari data tersebut.
- Sebuah toko elektronik mencatat penjualan produk dalam seminggu: 15 unit, 12 unit, 18 unit, 15 unit, 20 unit, 15 unit. Berapakah modus penjualan produk dalam seminggu?
Untuk pembahasan dari contoh-contoh soal di atas:
- Pada data nilai ujian matematika, modus adalah 82. Karena nilai 82 muncul paling sering, yaitu 3 kali.
- Pada data pengeluaran rumah tangga, modus adalah Rp 2.500.000. Nilai ini muncul 2 kali, lebih banyak daripada nilai lainnya.
- Pada data penjualan produk, modus adalah 15 unit. Nilai ini muncul 3 kali, lebih banyak daripada nilai lainnya.
- Melalui contoh soal modus dan pembahasannya di atas, Anda dapat berlatih menghitung dan mengidentifikasi modus dari berbagai jenis data dalam matematika dan statistika.
Cara Menghitung Modus
Menghitung modus relatif sederhana, namun metode yang digunakan bisa berbeda tergantung pada jenis data yang dianalisis:
- Data Kategorikal: Untuk data kategorikal, modus adalah kategori yang paling sering muncul. Misalnya, dalam survei mengenai warna favorit, warna yang paling banyak dipilih oleh responden adalah modus.
- Data Kuantitatif Diskret: Dalam data kuantitatif diskret, modus adalah nilai yang paling sering muncul. Jika data mencatat jumlah produk yang terjual setiap hari, modus adalah jumlah produk yang paling sering terjual.
- Data Kuantitatif Kontinu: Untuk data kuantitatif kontinu, perhitungan modus dapat melibatkan pembuatan histogram atau distribusi frekuensi. Modus adalah interval atau titik yang memiliki frekuensi tertinggi dalam histogram.
Contoh Perhitungan Modus
Mari kita lihat beberapa contoh perhitungan modus untuk lebih memahami konsep ini:
Contoh 1: Data Kategorikal
Misalkan kita memiliki data tentang warna mobil yang paling banyak dipilih oleh pelanggan dalam sebuah survei:
- Merah: 15
- Biru: 10
- Hitam: 15
- Putih: 5
Dalam contoh ini, warna merah dan hitam masing-masing muncul 15 kali, yang merupakan frekuensi tertinggi. Oleh karena itu, dataset ini memiliki dua modus: merah dan hitam (bimodal).
Contoh 2: Data Kuantitatif Diskret
Misalkan data mengenai jumlah buku yang dibaca oleh sekelompok orang dalam sebulan adalah:
- 3, 5, 3, 7, 3, 8, 9
Dalam hal ini, angka 3 muncul paling sering (3 kali). Jadi, modus dari data ini adalah 3.
Contoh 3: Data Kuantitatif Kontinu
Jika kita memiliki data tinggi badan siswa yang dibagi dalam interval:
- 140-150 cm: 5 siswa
- 151-160 cm: 20 siswa
- 161-170 cm: 25 siswa
- 171-180 cm: 10 siswa
Interval 161-170 cm memiliki frekuensi tertinggi. Oleh karena itu, modus dari data ini adalah interval 161-170 cm.
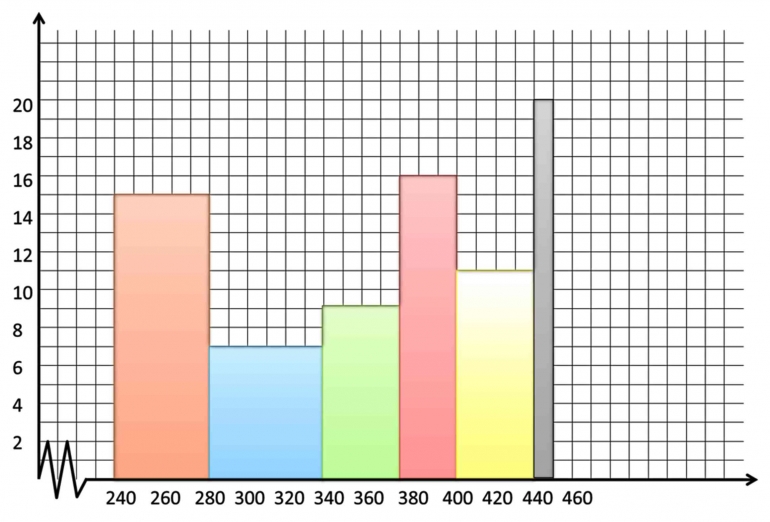
Modus dalam Distribusi Normal
Dalam statistika, modus sangat penting untuk memahami distribusi data, termasuk distribusi normal. Distribusi normal adalah model statistik yang penting dan digunakan di banyak bidang. Modus, sebagai ukuran pemusatan, terkait erat dengan mean dan median dalam distribusi normal.
Hubungan Modus dengan Mean dan Median pada Distribusi Normal
Pada distribusi normal simetris, modus, mean, dan median sama. Ini menunjukkan data terpusat dan seimbang. Ini berarti nilai yang paling sering muncul, rata-rata, dan nilai tengah sama.
Pada distribusi normal tidak simetris, modus, mean, dan median berbeda. Modus di titik puncak, sementara mean dan median di titik lain. Ini memberi info tentang kemiringan dan kurtosis data.
Mengerti hubungan modus, mean, dan median penting dalam statistika dan analisis data. Ini membantu analis untuk mengerti distribusi data dan membuat kesimpulan yang akurat.
Epilog
Modus adalah ukuran statistik yang sederhana namun sangat berguna dalam memahami distribusi data. Apa itu modus dalam matematika? Modus memberikan informasi tentang nilai yang paling sering muncul dalam sebuah dataset, yang bisa sangat berguna dalam berbagai konteks analisis. Dengan pemahaman yang baik tentang modus, kita dapat lebih efektif dalam menganalisis dan menginterpretasi data.
Dalam praktiknya, modus sering digunakan bersamaan dengan ukuran statistik lainnya seperti rata-rata dan median untuk memberikan gambaran yang lebih lengkap tentang data. Dengan menggunakan ketiga ukuran ini, kita dapat memperoleh pemahaman yang lebih baik tentang distribusi dan pola dalam data yang kita analisis.
