Memahami Pembagian dengan Bilangan Nol dan Bilangan Tak Hingga Melalui Sebuah Cake Cokelat

Bilangan Nol dan bilangan Tak Hingga merupakan dua buah bilangan yang sering terabaikan namun tetap dibutuhkan keberadaannya dalam memberikan solusi-solusi terhadap permasalahan yang ada di segala bidang, khususnya dalam Bidang Keteknikan. Sebagai contoh, bilangan Nol dan Tak Hingga menjadi parameter-parameter utama dalam menganalisa permasalahan yang berkaitan dengan fungsi dan limit.

Bilangan Nol merupakan bagian dari bilangan bulat, komplemen irisan dari bilangan cacah dan bilangan asli, dan dinyatakan dengan lambang “0”. Jumlah yang nihil dan kosong disebut sebagai bilangan Nol. 

Bilangan Tak Hingga menyatakan sesuatu yang tanpa batas (infinity). Bilangan Tak Hingga adalah bilangan yang sangat besar, jauh lebih besar dan melebihi bilangan real, dan dilambangkan dengan simbol “∞”. Karena dasarnya menyatakan sesuatu bilangan, maka bilangan tak hingga memiliki nilai negatif (- ∞) dan nilai positif (+ ∞).

A. Pembagian dengan Bilangan Nol

Aritmatika bilangan real menyatakan bahwa setiap pembagian yang dilakukan dengan bilangan Nol akan memberikan hasil yang tak terdefinisi atau tidak memiliki jawaban yang logis, sehingga tidak diperbolehkan untuk melakukan pembagian dengan angka Nol. Namun ada juga pemikiran lain berdasarkan pemahaman bahwa sebuah bilangan x jika dibagi dengan Tak Hingga menghasilkan bilangan Nol, karenanya jika sebuah bilangan x dibagi dengan Nol maka hasilnya adalah Tak Hingga. 

B. Pembagian dengan Bilangan Tak Hingga

Seperti yang telah dijelaskan sebelumnya, bilangan Tak Hingga memiliki nilai yang sangat besar dan lebih luas dari bilangan real. Jadi bila sebuah bilangan a dibagi dengan bilangan Tak Hingga, maka dapat diartikan banwa bilangan a tersebut dibagi dengan bilangan yang sangat besar nilainya, sehingga hasil yang didapat akan mendekati sebuah nilai yang sangat kecil, mendekati bilangan Nol. 

Untuk memahami lebih jauh tentang pembagian dengan bilangan Nol dan bilangan Tak Hingga, mari kita belajar melalui ilustrasi sebuah cake cokelat.

C. Ilustrasi Pembagian dengan Bilangan Nol

Misalkan ada sebuah cake cokelat yang tersedia di atas meja. Cake cokelat yang masih utuh dan belum dibagi kita nyatakan sebagai bilangan 1 (satu).

dokumentasi pribadi

Sekarang kita diminta untuk membagi kue tersebut menjadi 2 (dua) bagian.

Dokumentasi pribadi

Setelah dibagi 2 (dua), cake cokelat tersebut menjadi dua bagian yang sama dengan masing-masing bagian bernilai ½. Selanjutnya kita diminta untuk membagi kue tersebut menjadi empat bagian yang sama.

dokumentasi pribadi

Setelah dibagi 4 (empat), cake cokelat tersebut memiliki empat bagian yang sama dengan masing-masing bagian bernilai ¼. 

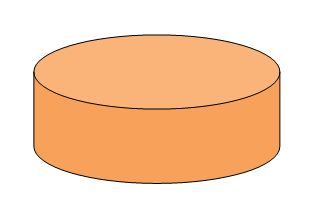
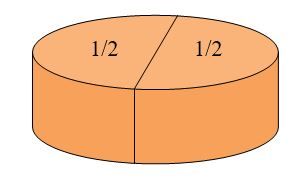
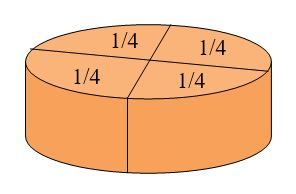
Sekarang bagaimana jika kita diminta untuk membagi cake tersebut menjadi Nol bagian, yang berarti 1 dibagi dengan 0? Bilangan Nol menyatakan bahwa tidak ada cake lagi yang tersisa atau tidak ada cake yang tersedia di atas meja. Bagaimana caranya kita membagi cake tersebut sehingga ‘hilang’ dari atas meja? Suatu hal yang tidak masuk akal, bukan? Cake cokelat itu akan selalu berada di atas meja jika kita melakukan pembagian (memotong menjadi beberapa bagian).

dokumentasi pribadi

Cake tidak akan hilang atau habis selama kita melakukan pembagian, kecuali jika kita memakannya. Kita diminta untuk membagi cake tersebut, dan bukan memakannya. Pemahaman yang lain yang mempertegas adalah bahwa pada awalnya sebuah cake itu selalu utuh dan bernilai 1 (satu). Itulah sebabnya mengapa membagi cake dengan bilangan 0 adalah hal yang tidak mungkin, dalam hal ini tak terdefinisikan. 

D. Ilustrasi Pembagian dengan Bilangan Tak Hingga

Bagaimana jika kita diminta membagi cake tersebut menjadi Tak Berhingga, yaitu 1 dibagi dengan ∞ ? Maksudnya adalah kita diminta untuk membagi cake tersebut menjadi Tak Hingga bagian, atau dengan kata lain cake dibagi menjadi bagian-bagian yang sangat banyak.

dokumentasi pribadi

Coba kita menganalisa hasil pembagian sebelumnya. Saat dibagi menjadi 4 bagian, potongan kue menjadi lebih kecil dibandingkan saat dibagi menjadi 2 bagian, maka secara logika dapat dipahami bahwa semakin besar jumlah yang akan dibagi, semakin kecil potongan kue yang dihasilkan, sehingga jika cake tersebut dibagi menjadi Tak Hingga, maka potongan cake akan menjadi sangat kecil dan dapat menyerupai ukuran sel-sel tubuh kita.

Ukuran yang sangat kecil tersebut jika ditarik limitnya, akan mendekati bilangan Nol. Dengan demikian, cukup jelas bahwa jika sebuah bilangan dibagi dengan Tak Hingga, akan menghasilkan bilangan Nol.

Ilustrasi ini menyimpulkan pemahaman bahwa Bilangan Nol adalah bilangan yang tidak memiliki nilai tentu, atau bobotnya kosong. Bilangan Tak Hingga adalah bilangan yang memiliki nilai tentu yang sangat besar dan tidak dapat ditentukan dengan pasti nilainya karena melampaui besaran yang dapat dihasilkan oleh bilangan real. Setiap bilangan yang dibagi dengan angka Nol akan menghasilkan nilai yang tak terdefinisi, sebaliknya setiap bilangan yang dibagi dengan Tak Hingga, kecuali bilangan Tak Hingga itu sendiri, akan menghasilkan nilai yang mendekati bilangan Nol. 

Semoga penjelasan ini bermanfaat. Nantikan tulisan berikutnya yang masih berkaitan dengan Nol dan Tak Hingga.

Terima Kasih.