Arah Mengikuti Jalur Orthodrom Serta Koreksi Ellipsoid Bumi Terhadap Arah Kiblat

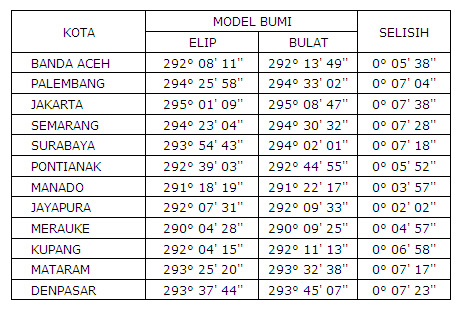
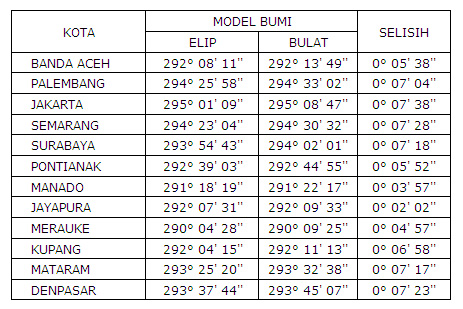
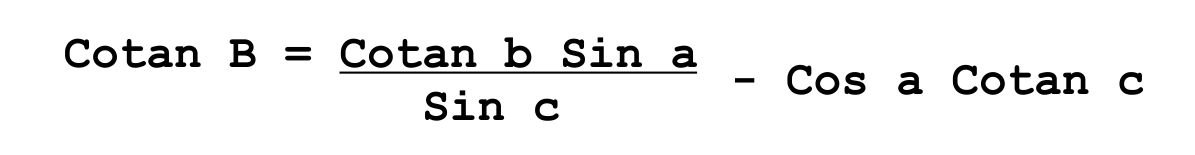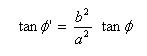Perhitungan sudut arah kiblat seperti diatas umumnya menggunakan acuan bahwa bumi adalah bulat penuh seperti bola, padahal menurut teori terkini bumi tidaklah bulat penuh namun sedikit elip atau lonjong seperti telur.  Jari-jari bumi antar kutub lebih pendek daripada jari khatulistiwa. Jari-jari khatulistiwa 6.378,1 km sementara Jari-jari kutub 6.356,8 km. Berikut beberapa referensi elipsoid bumi :

Referensi terbaru yang banyak dipakai untuk pengukuran adalah adalah WGS84 dengan nilai jari-jari 6378137 flattening inverse (pemampatan) 298,257223563.

Rumus segitiga di atas berlaku pada titik-titik di bidang permukaan bola. Sedangkan kenyataannya, koordinat tempat berada pada bidang elipsoid bumi. Sehingga apabila tidak dilakukan koreksi dari koordinat geografik ke koordinat geosentrik maka akan terjadi kesalahan meskipun hanya beberapa menit busur.

Untuk perhitungan yang lebih teliti, maka koordinat lintang geografik (Lt) dikoreksi atau dikonversikan ke koordinat lintang geosentrik (Lt')  dengan rumus sebagai berikut:

Berikut formula perhitungan arah kiblat dengan koreksi ellipsoid bumi yang diurai dari rumus vincenty dengan acuan ellipsoid WGS84.

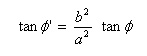
Contoh perhitungan arah kiblat metode vincenty untuk kota SURABAYA

Lt K            : 21° 25' 18,89" LU;      λ K                    : 39° 49' 46,27" BT
Lt               : 7° 15 ' LS;                 λ                       : 112° 45' BT

a               : 6378137                    (semi mayor axis ellipsoid)
f                : 0,003352810665       (flattening ellipsoid)
b               : a * (1 – f )                             = 6356752.314                        (semi minor axis ellipsoid)
U1             : tan-1 (1- f ) * tan ( f K )          = 21,35656982
U2             : tan-1 (1- f ) * tan ( f )             = -7,22594948
L0             : λ - λ K                                    = 72,92048056

cos σ         : sin U1* sin U2 + cos U1 * cos U2 * cos L0   = 0,225552214
sin σ          : √((cos U2 *sin L0)^2 +(cos U1 * sin U2 – sin U1 * cos U2 *cos L0)^2) = 0,974231081
σ               : tan-1 (1 sin σ / cos σ )                                 = 76,96464756
sin α          : (cos U1 * cos U2 *sin L0) / sin σ                   = 0,906548773
cos 2 α      : 1 - sin α^2                                                  = 0,178169322
cos (2σm)  : cos σ - 2 * sin  U1 * sin U2 / cos 2 α              = 0,739741189
C               : f /16 * cos 2 α * (4 + f  * (4 - 3 * cos 2 α))   = 0,0001497758073
L1              : L0+ (1 - C) * f * sin α * (σ + C * sin α * (cos (2σm)+C * cos σ * (-1 + 2 * cos (2σm) ^ 2)))
                     = 73,1543788451604

Ulangi perhitungan L dengan mengambil nilai L terakhir sampai selisih nilai antara L terakhir dengan L sebelumnya 0,000000000000 (digit ke-12 setelah koma nilainya nol)

cos σ         : sin U1* sin U2 + cos U1 * cos U2 * cos L1   = 0,221944529
sin σ          : √((cos U2 *sin L1)^2 +(cos U1 * sin U2 – sin U1 * cos U2 *cos L1)^2) = 0,975059294
σ               : tan-1 (1 sin σ / cos σ )                                 = 77,17672976
sin α          : (cos U1 * cos U2 *sin L1) / sin σ                   = 0,906907303
cos 2 α      : 1 - sin α^2                                                  = 0,177519144
cos (2σm)  : cos σ - 2 * sin  U1 * sin U2 / cos 2 α              = 0,738016764
C              : f /16 * cos 2 α * (4 + f  * (4 - 3 * cos 2 α))    = 0,0001492294860
L2             : L1+ (1 - C) * f * sin α * (σ + C * sin α * (cos (2σm)+C * cos σ * (-1 + 2 * cos (2σm) ^ 2)))      
                   = 73,1551162552349