Pengolahan Citra Digital

TUGAS MANDIRI

TUTORIAL OPERASI GEOMETRIK

MATA KULIAH : PENGOLAHAN CITRA DIGITAL

 

 

 

 

          Nama                             : Maeka R Pakpahan          

           Npm                                :  130210054              

           Kode Kelas                    :   142-TI28T-M5A

           Dosen                             :   Bpk Cosmas Eko Suharyanto, S.Kom.

 

 

 

PROGRAM STUDI TEKNIK INFORMATIKA

UNIVERSITAS PUTERA BATAM

2015

 

 

KATA PENGANTAR

 

Syukur kepada Tuhan Yang Maha Esa yang telah melimpahkan segala rahmat dan karunia-Nya, sehingga penulis dapat menyelesaikan Tugas Mandiri mata kuliah Pengolahan Citra Digital “ Tutorial Operasi Geometrik “. Penulis sadar bahwa makalah ini jauh dari sempurna. Karena itu kritik dan saran sangat penulis butuhkan demi kemajuan bersama.

Dengan segala keterbatasan penulis juga menyadari Tugas Mandiri ini tidak akan terselesaikan tanpa bantuan dan bimbingan dari berbagai pihak. Untuk itu penulis menyampaikan ucapan terima kasih kepada :

1. Bpk Cosmas Eko Suharyanto, S.Kom. selaku dosen mata kuliah

Pengolahan Citra Digital

1. Rekan mahasiswa yang memberikan dukungan dan semangat
2. Orangtua yang selalu memberikan restu dan doa

Semoga Tuhan Yang Maha Esa membalas kebaikan dengan mencurahkan berkat dan rahmat-Nya.

 

 

 

 

                                                                                                                                            Batam, 28 Juni 2015

 

                                                                                                                                Penyusun

 

 

 

DAFTAR ISI

KATA PENGANTAR.. 2

1.1 Pengantar Operasi Geometrik. 4

1.2 Menggeser Citra. 5

1.3 Memutar Citra. 7

1.4 Interpolasi Piksel 9

1.5 Memutar Berdasarkan Sebarang Koordinat 12

1.6 Memutar Citra Secara Utuh. 14

1.7 Memperbesar Citra. 17

1.8 Memperkecil Citra. 19

1.9 Perbesaran dengan Skala Vertikal dan Horizontal Berbeda. 19

1.10 Pencerminan Citra. 19

1.12 Efek Ripple. 23

1.14 Transformasi Spherical 25

1.15 Transformasi bilinear 28

DAFTAR PUSTAKA.. 30

 

 

 

 

 

 

 

 

 

 

 

 

1.1 Pengantar Operasi Geometrik

       Operasi geometrik adalah operasi pada citra yang dilakukan secara geometris seperti translasi, rotasi, dan penyekalaan.Pada operasi seperti ini terdapat pemetaan geometrik, yang menyatakan hubungan pemetaan antara piksel pada citra masukan dan piksel pada citra keluaran. Secara prinsip, terdapat dua cara yang dapat dipakai. Pertama yaitu pemetaan ke depan dan kedua berupa pemetaan ke belakang. Perbedaan secara visual kedua cara tersebut diperlihatkan pada Gambar 1.1.

Gambar 5.1Pemetaan geometrik    

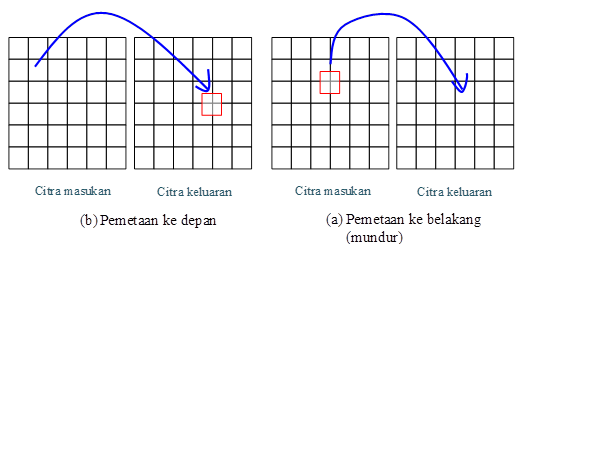
       Gambar di atas menjelaskan bahwa pada cara pemetaan ke depan, posisi pada citra keluaran ditentukan dengan acuan pemrosesan pada citra masukan. Pada gambar tersebut terlihat bahwa kalau piksel keluaran berada pada posisi yang tidak tepat (tidak berupa bilangan bulat),penempatannyadapat berada pada salah satu dari empat kemungkinan. Dengan cara seperti ini, ada kemungkinan sebuah piksel pada citra keluaran tidak pernah diberi nilai atau malah diberi nilai lebih dari satu kali. Hal ini berbeda dengan pada pemetaan ke belakang.Pada pemetaan ke belakang, mengingat pemrosesan dimulai dari citra keluaran maka dipastikan bahwa semua piksel pada citra keluaran akan diberi nilai sekali saja berdasarkan piksel masukan.

  Pada Gambar 1.1(a), piksel yang digunakan untuk menentukan piksel keluaran dapat ditentukan oleh salah satu piksel yang tercakup dalam kotak yang menggantung pada keempat piksel. Hal itu merupakan caratersederhana yang dapat dilakukan dan biasa dinamakan sebagai pemilihan berdasarkan tetangga terdekat. Cara lain yang dapat dilakukan adalah dengan memperhitungkan empat piksel yang dapat mewakilinya. Cara ini dikenal dengan sebutan interpolasi bilinear, yaitu linear di arah vertikal dan mendatar. Kedua cara ini akan dibahas saat membicarakan pemutaran citra (Subbab 1.3).

1.2 Menggeser Citra

       Penggeseran citra ke arah mendatar atau vertikal dapat dilaksanakan dengan mudah. Rumus yang digunakan sebagai berikut:

Untuk penyederhanaan pembahasan, sx dan sy dianggap bertipe bilangan bulat.

       Contoh berikut menunjukkan program yang digunakan untuk melakukan penggeseran citra.

% GESER Melakukan operasi penggeseran citra.

F = imread('c:\Image\pcd.png');

[tinggi, lebar] = size(F);

 

sx = 45; % Penggesaran arah horisontal

sy = -35; % Penggesaran arah vertikal

 

F2 = double(F);

G = zeros(size(F2));

for y=1 : tinggi

   for x=1 : lebar

       xlama = x - sx;

       ylama = y - sy;

       if (xlama>=1) && (xlama<=lebar) && ...

           (ylama>=1) && (ylama<=tinggi)

           G(y, x) = F2(ylama, xlama);

       else

           G(y, x) = 0;

       end

   end

end

G = uint8(G);

figure(1); imshow(G);

 

       Pada contoh di atas, citra digeser ke kanan sebesar 45 piksel (ditentukan melalui sx) dan ke atas sebesar 35 piksel (diatur melalui sy). Apabila xlama hasil perhitungan di luar jangkauan [1, lebar] atau ylama hasil perhitungan di luar jangkauan [1, tinggi], intensitas piksel pada posisi (y, x) diisi dengan nol (warna hitam). Posisi yang tidak berada pada posisi koordinat yang valid dalam citra lama akan diisi dengan nilai nol melalui

       G(y, x) = 0;

Hasilnya diperlihatkan pada Gambar 1.2.

 

• Citra pcd asli                                                      (b) Hasil pergeseran

Gambar 1.2Contoh penggeseran citra

Gambar hitam di bagian kiri dan bagian atas adalah efek dari pergeseran citra

1.3 Memutar Citra

       Suatu citra dapat diputar dengan sudut seiring arah jarum jam atau berlawanan arah jarum jam dengan pusat putaran pada koordinat (0,0). Gambar 1.3 menjelaskan bentuk pemutaran citra. Adapun rumus yang digunakan untuk memutar citra dengan sudut berlawanan arah jam berupa:

 

 

                                                      

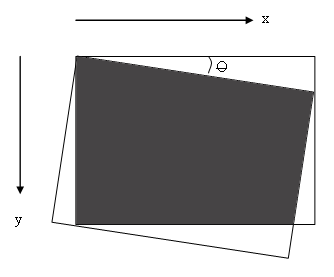
Gambar 1.3Pemutaran citra dengan pusat (0, 0)

       Berdasarkan Persamaan 1.3 dan 1.4, pemutaran citra dengan sudut searah jarum jam dapat dilakukan.Caranya, dengan menggunakan x dan y sebagai posisi baru dan xbaru justru sebagai posisi lama.Pada saat menghitung dengan rumus di atas, apabila posisi koordinat (ybaru ,xbaru) berada di luar area [1, lebar] dan [1, tinggi], intensitas yang digunakan berupa nol. Cara inilah yang merupakan contoh pemetaan ke belakang. Implementasinya dapat dilihat berikut ini.

F = imread('c:\Image\pcdabu.png');

[tinggi, lebar] = size(F);

sudut = 10; % Sudut pemutaran

rad = pi * sudut/180;

cosa = cos(rad);

sina = sin(rad);

F2 = double(F);

for y=1 : tinggi

   for x=1 : lebar  

       x2 = round(x * cosa + y * sina);      

       y2 = round(y * cosa - x * sina);        

       if (x2>=1) && (x2<=lebar) && ...

           (y2>=1) && (y2<=tinggi)

           G(y, x) = F2(y2, x2);

       else  

           G(y, x) = 0;

       end

   end

end

G = uint8(G);

figure(1); imshow(G);

Contoh hasil pemutaran dapat dilihat pada Gambar 1.4.

                                                                               

• Citra pcdabu asli                                                    (b) Setelah pemutaran

 

Gambar 1.4Contoh pemutaran citra

1.4 Interpolasi Piksel

       Hasil pemutaran citra menggunakan rotasi.m menimbulkan efek bergerigi pada objek citra.Hal itu diakibatkan oleh penggunaan nilai intensitas didasarkan pada piksel tetangga terdekat, yang dilakukan melalui:

 

x2 = round(x * cosa + y * sina);      

y2 = round(y * cosa - x * sina);      

 

Penggunaan fungsi round (pembulatan ke atas) merupakan upaya untuk menggunakan intensitas piksel terdekat.Alternatif laindilakukan dengan menggunakan floor (pembulatan ke bawah).

Keadaan seperti itu dapatdiperhalus melalui interpolasi piksel.

       Idenya seperti berikut. Misalnya, hasil perhitungan menghasilkan

 

       xlama = 47,09

       ylama = 59,85

Gambar 1.7Model pendekatan bilinear interpolation

 

Perhatikan bahwa f(p’. q’) mempunyai empat piksel terdekat berupa f(p,q), f(p,q+1), f(p+1,q), dan f(p+1,q+1).

       Pratt (2001) menunjukkan cara menghitung nilai intensitas yang digunakan untuk suatu piksel berdasarkan empat piksel. Rumusnya sebagai berikut

Dalam hal ini, a dan b dihitung melalui:

Rumus dalam Persamaan 1.5 itulah yang disebut sebagai bilinear interpolation.

       Contoh program yang menggunakan interpolasi bilinear untuk mendapatkan intensitas piksel dapat dilihat di bawah ini.

 

F = imread('c:\Image\pcdabu.png');

[tinggi, lebar] = size(F);

sudut = 15; % Sudut pemutaran

rad = pi * sudut/180;

cosa = cos(rad);

sina = sin(rad);

F2 = double(F);

for y=1 : tinggi

for x=1 : lebar  

x2 = x * cosa + y * sina;      

       y2 = y * cosa - x * sina;      

if (x2>=1) && (x2<=lebar) && ...

           (y2>=1) && (y2<=tinggi)

           % Lakukan interpolasi bilinear

           p = floor(y2);

           q = floor(x2);

           a = y2-p;

           b = x2-q;

if (x2 == lebar) || (y2 == tinggi)

             G(y, x) = F(floor(y2), floor(x2));

else

intensitas = (1-a)*((1-b)*F(p,q) + ...

b * F(p, q+1)) +     ...

a *((1-b)* F(p+1, q) + ...

b * F(p+1, q+1));

             G(y, x) = intensitas;

end

else

           G(y, x) = 0;

end

end

end

G = uint8(G);

figure(1); imshow(G);

 

       Gambar 1.8 memperlihatkan perbedaan hasil antara pemutaran citra yang menggunakan pendekatan interpolasi bilinear dan yang tidak.

   

        

(a)Gambar pcdabu asli                                                  (b) dengan interpolasi

Gambar 1.8Perbandingan efek penggunaan interpolasi bilinear

 

1.5 Memutar Berdasarkan Sebarang Koordinat

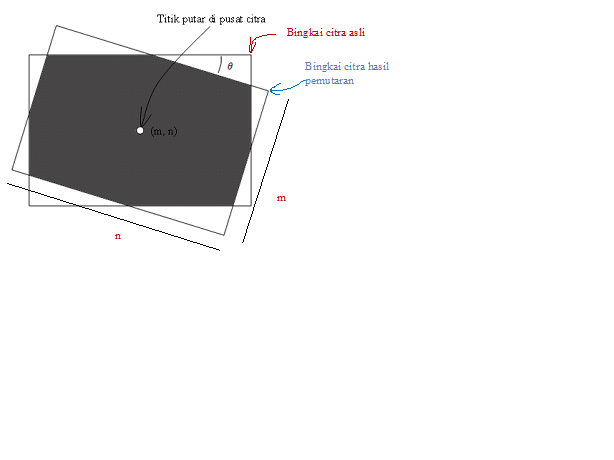
       Operasi pemutaran citra dapat dilakukan dengan pusat di mana saja; tidak harus dari (0, 0).Gambar 1.9 memperlihatkan keadaan ini.

Gambar 1.9Pemutaran citra melalui titik pusat citra

 

       Rumus untuk melakukan pemutaran berlawanan arah jarum jam sebesar qyang diperlihatkan pada Gambar 1.9diperoleh melalui pemodifikasian Persamaan 5.3 dan 5.4:

 

 

                

 

       Untuk kepentingan pemutaran citra sejauh searah jarum jam, intensitas piksel (y,x) dapat diperoleh melalui intensitas pada piksel (ybaru, xbaru) yang tertera pada Persamaan 1.8 dan 1.9.Implementasi program dapat dilihat pada contoh berikut.

 

 

F = imread('c:\Image\pcdabu.png');

[tinggi, lebar] = size(F);

 

sudut = 5; % Sudut pemutaran

rad = pi * sudut/180;

cosa = cos(rad);

sina = sin(rad);

F2 = double(F);

 

m = floor(tinggi / 2);

n = floor(lebar / 2);

 

for y=1 : tinggi

for x=1 : lebar  

x2 = (x-n) * cosa + (y-m) * sina + n;      

       y2 = (y-m) * cosa - (x-n) * sina + m;    

if (x2>=1) && (x2<=lebar) && ...

           (y2>=1) && (y2<=tinggi)

           % Lakukan interpolasi bilinear

           p = floor(y2);

           q = floor(x2);

           a = y2-p;

           b = x2-q;

 

if (x2==lebar) || (y2 == tinggi)

             G(y, x) = F(y2, x2);

else

intensitas = (1-a)*((1-bF(p,q) + ...

b * F(p, q+1)) +     ...

a *((1-b)* F(p+1, q) + ...

b * F(p+1, q+1));

 

             G(y, x) = intensitas;

end

else

           G(y, x) = 0;

end

end

end

G = uint8(G);

figure(1); imshow(G);

 

1.6 Memutar Citra Secara Utuh

       Pada seluruh contoh yang telah diberikan, ada bagian gambar yang hilang ketika pemutaran dilaksanakan.Namun, adakalanya dihendaki agar pemutaran citra tidak membuat ada bagian citra asli hilang. Untuk keperluan ini, ukuran citra hasil pemutaran harus diubah sesuai dengan sudut putaran.Dalam hal ini, Persamaan 1.8 dan 1.9 digunakan untuk menentukan keempat pojok gambar semula.Adapun lebar dan tinggi gambar hasil pemutaran dengan menghitung nilai terkecil dan terbesar dari koordinat keempat pojok hasil pemutaran.Untuk lebih jelasnya, lihat Gambar 1.11.

Gambar 1.11Penentuan lebar dan tinggi citra hasil pemutaran

 

F = imread('c:\Image\pcdabu.png');

[tinggi, lebar] = size(F);

sudut = 45; % Sudut pemutaran

rad = pi * sudut/180;

cosa = cos(rad);

sina = sin(rad);

x11 = 1;     y11 = 1;

x12 = lebar; y12 = 1;

x13 = lebar; y13 = tinggi;

x14 = 1;     y14 = tinggi;

m = floor(tinggi/2);

n = floor(lebar/2);

% Menentukan pojok

x21 = ((x11-n) * cosa + (y11-m) * sina + n);

y21 = ((y11-m) * cosa - (x11-n) * sina + m);        

 

x22 = ((x12-n) * cosa + (y12-m) * sina + n);

y22 = ((y12-m) * cosa - (x12-n) * sina + m);        

 

x23 = ((x13-n) * cosa + (y13-m) * sina + n);

y23 = ((y13-m) * cosa - (x13-n) * sina + m);        

 

x24 = ((x14-n) * cosa + (y14-m) * sina + n);

y24 = ((y14-m) * cosa - (x14-n) * sina + m);        

 

ymin = min([y21 y22 y23 y24]);

xmin = min([x21 x22 x23 x24]);

 

ymak = max([y21 y22 y23 y24]);

xmak = max([x21 x22 x23 x24]);

 

lebar_baru = xmak - xmin + 1;

tinggi_baru = ymak - ymin + 1;

tambahan_y = floor((tinggi_baru-tinggi)/2);

tambahan_x = floor((lebar_baru-lebar)/2);

F2=zeros(tinggi_baru, lebar_baru);

for y=1 : tinggi

for x=1 : lebar

       F2(y+tambahan_y, x+tambahan_x) = F(y, x);

end

end

 

figure(1);

imshow( uint8(F2));

 

% Putar citra

m = floor(tinggi_baru/2);

n = floor(lebar_baru/2);

 

for y=1 : tinggi_baru

for x=1 : lebar_baru  

x2 = round((x-n) * cosa + (y-m) * sina + n);      

       y2 = round((y-m) * cosa - (x-n) * sina + m);        

 

if (x2>=1) && (x2<=lebar_baru) && ...

           (y2>=1) && (y2<=tinggi_baru)

           G(y, x) = F2(y2,x2);

else

          G(y,x) = 0;

end

end

end

 

figure(2);

G = uint8(G);

 

imshow(G);

       

  

(a) Gambar pcdabu asli                                              (b) hasil pemutaran

1.7 Memperbesar Citra

       Suatu citra dapat diperbesar dengan membuat setiap piksel menjadi beberapa piksel. Gambar 5.13 memberikan contoh cara memperbesar citra.

 

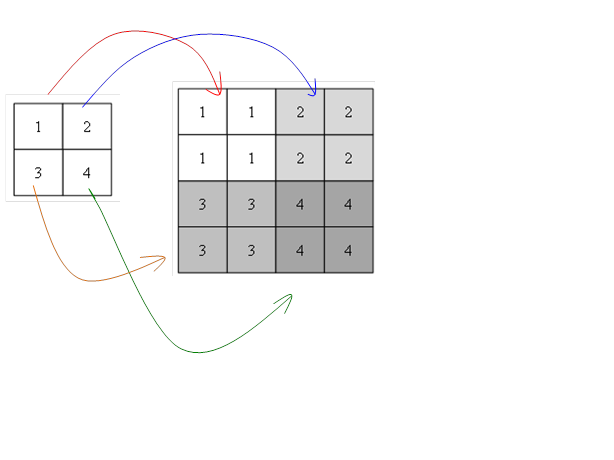
Gambar 1.13Cara memperbesar citra

Pada contoh di atas pembesaran pada arah vertikal dan horizontal sebesar 2 kali.

Berikut adalah fungsi yang memperlihatkan caraperbesarantersebut.

function G = perbesar(berkas, sy, sx)

F = imread(berkas);

[tinggi, lebar] = size(F);

tinggi_baru = tinggi * sy;

lebar_baru = lebar * sx;

F2 = double(F);

for y=1 : tinggi_baru

   y2 = ((y-1) / sy) + 1;

for x=1 : lebar_baru

x2 = ((x-1) / sx) + 1;

       G(y, x) = F(floor(y2), floor(x2));

end

end

G = uint8(G);

end

Img=perbesar('C:\Image\pcdabu.png', 3, 3);

imshow(Img);

      

  

(a) Gambar pcd asli                                          (b) Hasil Pembesaran

 

1.8 Memperkecil Citra

       Bagaimana kalau ingin memperkecil citra?Secara prinsip, pengecilan citra berarti mengurangi jumlah piksel.Algoritma yang digunakan untuk mewujudkanperbesar.m maupun perbesar2.m dapat digunakan untuk keperluan ini dengan m berupa bilangan pecahan seperti 1/2, ¼, 1/8, dan seterusnya. Contoh:

>>Img=perbesar2('C:\Image\pcdabu.png', 0.5, 0.5);Ã

>>imshow(Img);Ã

 

1.9 Perbesaran dengan Skala Vertikal dan Horizontal Berbeda

       Fungsi perbesar dan perbesar2 dapat digunakan untuk melakukan perbesaran/pengecilan dengan skala horizontal dan vertikal yang berbeda. Sebagai contoh, dapatdiberikan perintah seperti berikut:

>>Img=perbesar2('C:\Image\pcdabu.png', 0.5, 2.5);Ã

>>imshow(Img);Ã

1.10 Pencerminan Citra

       Pencerminan yang umum dilakukan berupa pencerminan secara vertikal dan pencerminan secara horizontal.Pencerminan secara horizontal dilakukan dengan menukarkan dua piksel yang berseberangan kir-kanan, sebagaimana diperlihatkan pada Gambar 1.18.Algoritma untuk menangani pencerminan secara horizontal diperlihatkan Algoritma 1.1.

 

Gambar 1.18Pencerminan secara horizontal

 

ALGORITMA 1.1 – Mencerminkan gambar secara horizontal

Masukan:

·         f (M,N): Citra masukan berukuran M baris dan N kolom

Keluaran:

·         g (M, N): Hasil citra yang telah dicerminkan secara horizontal

 

1.       FOR baris ¬ 1 TO M

2.          FOR kolom ¬ 1 TO N

3.               g(baris, kolom) ¬ f(N – baris + 1, kolom)

4.       END-FOR

5.      END-FOR

 

Implementasinya ditunjukkan pada program berikut.

function G = cerminh(F)

[tinggi, lebar] = size(F);

for y=1 : tinggi

   for x=1 : lebar

       x2 = lebar - x + 1;

       y2 = y;

       G(y, x) = F(y2, x2);

   end

end

end

G = uint8(G);

F=imread('C:\Image\pcdabu.png');

G=cerminh(F); imshow(G)

Contoh pencerminan gambar secara horizontal ditunjukkan pada Gambar 1.19.

    

    

• Gambar pcdabu asli                                             (b) Hasil pencerminan

Gambar 1.19Pencerminan secara horizontal

       Pencerminan secara vertikal dilakukan dengan menukarkan dua piksel yang berseberangan atas-bawah, sebagaimana diperlihatkan pada Gambar 1.20.Algoritma untuk menangani pencerminan secara horizontal diperlihatkan Algoritma 1.2.

Gambar 1.20Pencerminan secara vertikal

 

ALGORITMA 1.2 – Mencerminkan gambar secara vertikal

Masukan:

·         f (M,N): Citra masukan berukuran M baris dan N kolom

Keluaran:

·         g (M, N): Hasil citra yang telah dicerminkan secara horizontal

 

1.      FOR baris ¬ 1 TO M

2.         FOR kolom ¬ 1 TO N

3.               g(baris, kolom) ¬ f(baris, N – kolom + 1)

4.         END-FOR

5.      END-FOR

 

Implementasinya ditunjukkan pada program berikut.

 

 

 

function G = cerminv(F)

% CERMINV Berfungsi untuk mencerminkan citra

%     secara vertikal

%     Masukan: F = Citra berskala keabuan

 

[tinggi, lebar] = size(F);

 

for y=1 : tinggi

   for x=1 : lebar

       x2 = x;

       y2 = tinggi - y + 1;

 

       G(y, x) = F(y2, x2);

   end

end

end

G = uint8(G);

F=imread('C:\Image\pcdabu.png');

G=cerminv(F); imshow(G)

Contoh pencerminan gambar secara vertikal ditunjukkan pada Gambar 1.21.

  

     

(a)Gambar pcdabu asli                                                                       (b)hasil pencerminan

Gambar 1.21Pencerminan secara vertikal

1.12 Efek Ripple

       Efek ripple (riak) adalah aplikasi transformasi citra yang membuat gambar terlihat bergelombang. Efek riakdapaat dibuat baik pada arah x maupun y. Transformasinya seperti berikut:

 

 

                                                                        

Dalam hal ini, ax dan ay menyatakan amplitudoriak gelombang sinus, sedangkan Tx dan Ty menyatakan periode gelombang sinus.

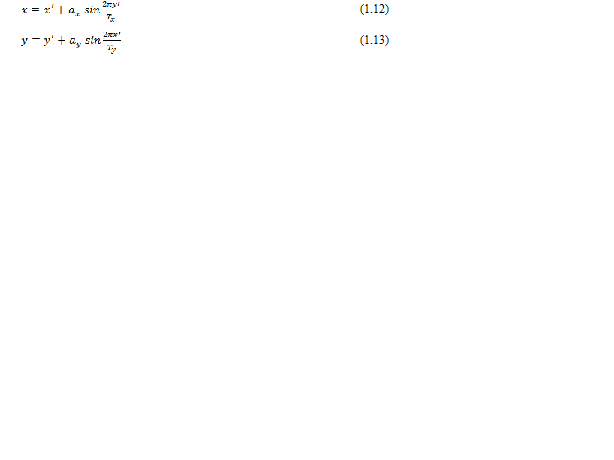
       Implementasi efek gelombang dapat dilihat di bawah ini.

 

function G = ripple(F, ax, ay, tx, ty)

% RIPPLE Berfungsi untuk melakukan transformasi 'ripple'.

 

dimensi = size(F);

tinggi = dimensi(1);

lebar = dimensi(2);

for y=1 : tinggi

   for x=1 : lebar

       x2 = x + ax * sin(2 * pi * y / tx);

       y2 = y + ay * sin(2 * pi * x / ty);

       if (x2>=1) && (x2<=lebar) && ...

           (y2>=1) && (y2<=tinggi)

 

           % Lakukan interpolasi bilinear

           p = floor(y2);

           q = floor(x2);

           a = y2-p;

           b = x2-q;

 

           if (floor(x2)==lebar) || ...

             (floor(y2) == tinggi)

             G(y, x) = F(floor(y2), floor(x2));

           else

             intensitas = (1-a)*((1-b)*F(p,q) + ...

             b * F(p, q+1)) +     ...

             a *((1-b)* F(p+1, q) + ...

             b * F(p+1, q+1));

             G(y, x) = intensitas;

           end

       else

           G(y, x) = 0;

       end  

   end

end

end

G = uint8(G);

F=imread('C:\image\pcdabu.png');

G=ripple(F,10,15,120, 250);

imshow(G)

Pada contoh di atas, amplitude gelombang sinus yang digunakan berupa 10 dan 15, sedangkan periode yang digunakan 120 dan 250.Contoh hasil perintah di atas ditunjukkan pada Gambar 1.23.

     

  

                       Gambar 1.23Contoh hasil efek ripple

1.14 Transformasi Spherical

       Transformasi spherical memberikan efek bulatan (bola), seperti melihat gambar menggunakan lensa pembesar.Bagian tengah terlihat membesar.Hal seperti itu diperoleh dengan menggunakan transformasi seperti berikut.

 

                              

 

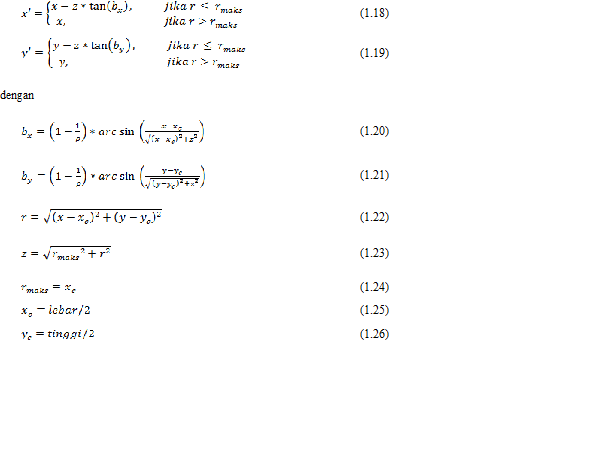
Perlu diketahui, disebut indeks refraksi atau indeks pantulan.

       Implementasi transformasi spherical dapat dilihat pada program berikut.

function G = spheri(F, rho)

% SPHERI Berfungsi untuk melakukan transformasi 'spherical'

 

dimensi = size(F);

tinggi = dimensi(1);

lebar = dimensi(2);

xc = round(lebar / 2);

yc = round(tinggi / 2);

 

rmaks = xc; % 1/2 lebar gambar

 

for y=1 : tinggi

   for x=1 : lebar

       r = sqrt((x-xc)^2+(y-yc)^2);

       z = sqrt(rmaks^2-r^2);

       bx = (1 - 1/rho) * asin((x-xc)/...

sqrt((x-xc)^2+z^2));

       by = (1 - 1/rho) * asin((y-yc)/...

sqrt((y-yc)^2+z^2));

       if r <= rmaks

           x2 = x - z * tan(bx);

           y2 = y - z * tan(by);

       else

           x2 = x;

           y2 = y;

       end

 

       if (x2>=1) && (x2<=lebar) && ...

           (y2>=1) && (y2<=tinggi)

 

           % Lakukan interpolasi bilinear

           p = floor(y2);

         q = floor(x2);

           a = y2-p;

           b = x2-q;

 

           if (floor(x2)==lebar) || ...

             (floor(y2) == tinggi)

             G(y, x) = F(floor(y2), floor(x2));

           else

             intensitas = (1-a)*((1-b)*F(p,q) + ...

             b * F(p, q+1)) +     ...

             a *((1-b)* F(p+1, q) + ...

             b * F(p+1, q+1));

 

             G(y, x) = intensitas;

           end

       else

           G(y, x) = 0;

       end  

   end

end

G = uint8(G);

end

F=imread('C:\Image\pcdabu.png');

G=spheri(F, 1.8); imshow(G)

Hasil ditunjukkan pada Gambar 5.26.

    

 

  

• Gambar pcdabu asli                                          (b) Hasil Transformasi

Gambar 1.26Transformasi spherical

 

 

1.15 Transformasi bilinear

       Transformasi bilinear mempunyai fungsi pemetaan seperti berikut:

 

                                                  

 

Transformasi ini termasuk dalam transformasi nonlinear mengingat terdapat pencampuran xy.Implementasi dalam bentuk program dapat dilihat berikut ini.

function G = tbilin(F, a1, a2, a3, a4, b1, b2, b3, b4)

% Fungsi untuk melakukan transformasi bilinear

dimensi = size(F);

tinggi = dimensi(1);

lebar = dimensi(2);

 

for y=1 : tinggi

   for x=1 : lebar

       x2 = a1 * x + a2 * y + a3 * x * y + a4;

       y2 = b1 * x + b2 * y + b3 * x * y + b4;

 

       if (x2>=1) && (x2<=lebar) && ...

           (y2>=1) && (y2<=tinggi)

 

           % Lakukan interpolasi bilinear

           p = floor(y2);

           q = floor(x2);

           a = y2-p;

           b = x2-q;

 

           if (floor(x2)==lebar) || ...

             (floor(y2) == tinggi)

             G(y, x) = F(floor(y2), floor(x2));

           else

             intensitas = (1-a)*((1-b)*F(p,q) + ...

             b * F(p, q+1)) +     ...

             a *((1-b)* F(p+1, q) + ...

             b * F(p+1, q+1));

 

             G(y, x) = intensitas;

           end

       else

           G(y, x) = 0;

       end  

   end

end

G = uint8(G);

end

F=imread('C:\Image\pcdabu.png');

G=tbilin(F, 1.2,0.1,0.005,-45,0.1,1,0.005,-30);

imshow(G)

Hasinya dapat dilihat pada Gambar 1.27.

       

         

  

• Gambar pcdabu asli                                              (b) Hasil transformasi

Gambar 1.27Transformasi bilinear

 

 

 

 

DAFTAR PUSTAKA

Acharya, T.; Ray, A.K. 2005; Image Processing Principles and Applications; New Jersey: John Wiley & Sons, Inc.

Aribowo, A.S.2009.Model Penelusuran Citra Digital pada Database Citra Menggunakan Pendekatan perhitungan Kedekatan Pola Warna.Prosiding Seminar Nasional Teknik Informatika e-Democracy, UPN Yogyakarta.

Abdul Kadir dan Adhi susanto, 2013, teori dan aplikasi pengolahan citra, penerbit andi yogyakarta.