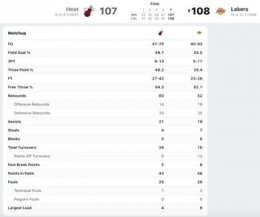
"Wade's guarding Bryant, Artest looking gets it to Bryant. Bryant dribbling, has to put it up for the buzzer. Bangs it in. He bangs in the three. And the Lakers win the game".
Kobe Bryant, the late Los Angeles Lakers great has always been known for his proclivity for delivering in crunch time. Kobe Bryant's game winners are always out of this world, and on December 4 2009, he delivered arguably one of the best shots of the decade.
The Lakers were just fresh off an NBA final and they were on a roll, winning seventh straight games in a row. However, the defending champion Lakers had to face defending scoring champion Dwyane Wade and the Miami Heat.
The two future Hall of Famers relentlessly exchanged buckets during the whole game. With less than two minutes to go in the game, it appeared as though the Lakers' winning streak may end. Bryant missed a potential game-tying shot after Wade handed the Heat a two-point advantage, thus forcing the Lakers to commit fouls. Miami would go on to hit free throws which puts them up by four. Then, with 4.3 seconds remaining in the game, Derek Fisher made a huge three-pointer to narrow the Miami lead to one. The Lakers fouled Wade, who converted one of his two free throw attempts, putting the Lakers in position for a possible victory.
With 3.2 seconds left and a two-point deficit, the Lakers passed the ball to Bryant, who immediately started dribbling towards his left. Wade pursued Kobe the entire play, not allowing him an inch of space, but Kobe miraculously scored a three-point shot while drifting to his left, delivering the Lakers an incredible one point victory.
This shot has an absurd degree of difficulty. Bryant's shot should have gone leftward, just as where his body was going, but he adjusted to knock the shot down. Even though the shot went in, why didn't Bryant and the Lakers try to shoot a two-point shot closer to the basket? Was shooting a three-point shot the best decision? Over time the study of economics has shown to give us insights about people's behavior, therefore, by using economic theory, namely game theory, this essay aims to answer these questions.
A Brief Explanation on Game Theory
Ultimately, economics is the study of choice. Economics encompasses every imagined aspect of human experience because options exist in every imagined area of human experience. Economists have investigated the nature of family life, education, politics, sports, and law---the list is practically endless since we spend far too much of our lives making decisions (University of Minnesota, 2016).
One of the tools to study choices in economics is game theory. Game theory is a conceptual framework for understanding social situations with competing players. Game theory is, in some senses, the study of strategy, or, more specifically, the optimal decision-making of autonomous and competing actors in a strategic environment (Hayes, 2021).
Game theory was created by American mathematician John von Neumann and German-born economist Oskar Morgenstern at Princeton University to address economic issues. In their 1944 book The Theory of Games and Economic Behaviour, Von Neumann and Morgenstern contended that the mathematics developed for physical sciences was an inadequate model for economics. Morgenstern and Von Neumann noticed that economics is analogous to a game in which players predict each other's movements, prompting the creation of a new field of mathematics known as game theory (Britannica, 2021).
Certain major properties of games, the most prominent of which is the total of players, can be classified. As a result, a game can be classed as a one-person, two-person, or n-person (with n greater than two) game, each having their own unique characteristics. Furthermore, a player is not always an individual; it may be a state, a company, or a group of people with similar interests. The contest in this case is between the Lakers and Heat. Besides, there are various types of game theory situations; in this case, it is referred to as a zero-sum game. In game theory, a zero-sum situation arises when one player's gain equals another's loss, resulting in no net change in benefit (Investopedia, 2020).
Game Theory Analysis
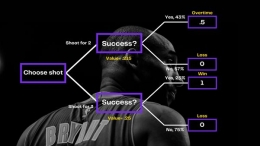
Using the "look forward, reason backward" method on this model, as shown in the diagram, reveals that the shooting team's prevailing strategy is to attempt a three-pointer. Given that the three-point shot is anticipated to be successful approximately one-fourth of the time and thus win the game immediately, the expected value (25 percent) is greater than the 43 percent possibility of a successful two-point shot times the 50 percent chance of winning in overtime (21.5 percent).
However, in one crucial aspect, this analysis oversimplifies the decision. It simply takes into account the activity of the shooting team and ignores the impact of the defending team's strategic decisions. But, with barely three seconds remaining on the clock, the Heat only sought to react to the Lakers offense only by fiercely protecting Bryant. They did not appear to be looking to entice the Lakers with a 2- or 3-point shot; rather, they seemed to adjust their play to the Lakers' offense.
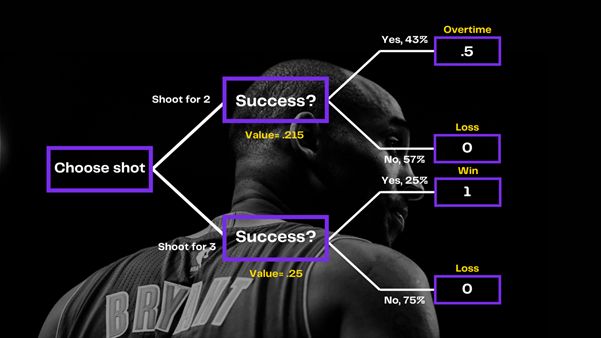
Simply put, by modelling the game using simple sequential analysis, attempting a three-point shot seems like the best decision for the Lakers. Therefore, Kobe Bryant's decision to take a three-point shot was the right one. However, we must remember that one needs luck -- a random variable yet so important for success -- to drill a game winning shot. In the end, it all comes down to the shooter (the one taking the game winning shot), knowing that the three-point shot is the best strategy, one must have courage, skill, and a mentality like no other. In this case it's Kobe Bryant, one of the best shooting guards of all time known as the hardest player in the world. It could be that he had practiced the shot hundreds of times.
Adrien Wida Devachandra | Undergraduate Economics Student at the University of Indonesia | Staff of Economic Studies Division at Kanopi FEB UI
Works Cited
Brams, S. J., & Davis, M. D. (2021, January 24). Game Theory. Encyclopedia Britannica. https://www.britannica.com/science/game-theory.
Chow, T., Miller, K., Nzima, S., & Winder, S. (2012). Game Theory (MBA 217) Final Paper. Game Theory - Meet the Berkeley-Haas Faculty. http://faculty.haas.berkeley.edu/rjmorgan/mba211/Chow%20Heavy%20Industries%20Final%20Project.pdf.
Hansford, C. (2020, December 4). This Day In Lakers History: Kobe Bryant Buzzer-Beater Over Dwyane Wade. Lakers Nation. https://lakersnation.com/this-day-lakers-history-kobe-bryant-buzzer-beater-over-dwyane-wade-heat/2020/12/04/.
Kenton, W. (2021, May 19). Zero-sum Game. Investopedia. https://www.investopedia.com/terms/z/zero-sumgame.asp.
Open Textbook Library. (2016). Principles of macroeconomics.
Ruminski, S. (2012, June 19). Game theory applied to basketball by Shawn Ruminski. Mind Your Decisions. https://mindyourdecisions.com/blog/2012/06/19/game-theory-applied-to-basketball-by-shawn-ruminski/.
Baca konten-konten menarik Kompasiana langsung dari smartphone kamu. Follow channel WhatsApp Kompasiana sekarang di sini: https://whatsapp.com/channel/0029VaYjYaL4Spk7WflFYJ2H