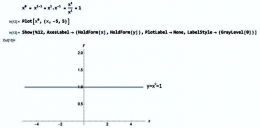
3. Mengapa setiap bilangan (termasuk 0) jika dipangkatkan dengan eksponen 0 selalu sama dengan 1?
Jawabannya sangat mudah tetapi selalu dilupakan. Lihat Gambar-03.
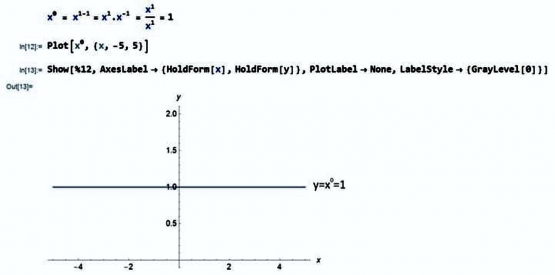
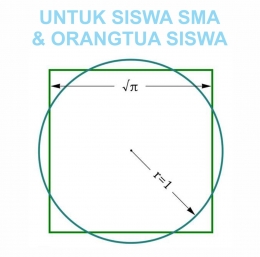
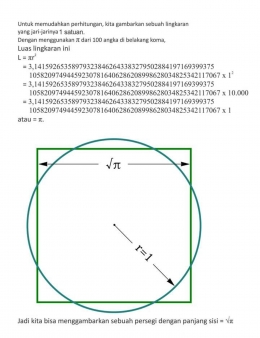
4. Apakah sebuah lingkaran bisa dijadikan persegi dengan luas yang sama?
Jawabannya: bisa dan tak bisa.
Apakah gambarnya benar? Bisa dibenarkan.
Apakah ukuran persegi itu 100% tepat? TIDAK!
Nah lho, mengapa demikian? Lihat Gambar-04.
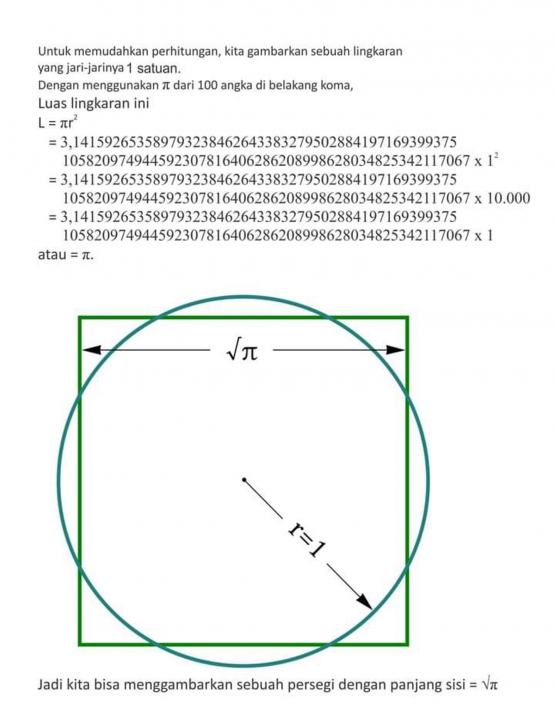
Catatan:
Teori diambil dari Squaring the circle. Pada 1882, π yang semula dianggap hanya merupakan sebuah bilangan irrasional dibuktikan dengan teorema Lindemann-Weierstrass sebagai sebuah bilangan transendental sekaligus bilangan irrasional aljabar. Jadi π hanya bisa digunakan untuk menggambarkan dengan tepat sebuah lingkaran berjari-jari tertentu, sambil masih dicari oleh matematikawan aproksimasi nilainya yang lebih tepat (membingungkan?). Karena π adalah transendental, maka √π juga transendental. Jadi persegi yang digambarkan dengan panjang sisi dari √π bisa dibenarkan jika panjang sisi tersebut ditulis "√π," bukan nilai aktualnya. Sebagaimana halnya π, √π adalah sebuah bilangan pecahan dengan angka di belakang koma yang tak berkesudahan, bagaimana mungkin ada alat ukur yang bisa dengan tepat mengukur panjang sisi persegi tersebut, seberapa besar pun persegi itu dibuat.
Pada 1882 teorema Lindemann–Weierstrass sudah membuktikan bahwa menjadikan sebuah lingkaran menjadi persegi dengan luas yang sama adalah hal yang tak mungkin. Ini π dalam 1,000 angka di belakang koma:
3,1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480865132823066470938446095505822317253594081284811174502841027019385211055596446229489549303819644288109756659334461284756482337867831652712019091456485669234603486104543266482133936072602491412737245870066063155881748815209209628292540917153643678925903600113305305488204665213841469519415116094330572703657595919530921861173819326117931051185480744623799627495673518857527248912279381830119491298336733624406566430860213949463952247371907021798609437027705392171762931767523846748184676694051320005681271452635608277857713427577896091736371787214684409012249534301465495853710507922796892589235420199561121290219608640344181598136297747713099605187072113499999983729780499510597317328160963185950244594553469083026425223082533446850352619311881710100031378387528865875332083814206171776691473035982534904287554687311595628638823537875937519577818577805321712268066130019278766111959092164201989
Selamat mendampingi anak belajar.
Sumber: Bahan pembelajaran anak saya tahun 2020.
Jonggol, 30 April 2021
Johan Japardi
Baca konten-konten menarik Kompasiana langsung dari smartphone kamu. Follow channel WhatsApp Kompasiana sekarang di sini: https://whatsapp.com/channel/0029VaYjYaL4Spk7WflFYJ2H