"Belajar bukan melulu memindahkan isi buku atau hal-hal yang diajarkan oleh guru ke dalam 'otak,' tetapi mengasah kemampuan mengamati dan pada gilirannya mengingat terus dari mana asal konsep yang sedang dipelajari, mempertanyakan, mengutak-atik, membolak-balik, mengait-ngaitkan konsep yang satu dengan konsep lainnya, dan menghafal dengan cara yang benar yang tidak membebani otak dan terus mengingatnya (proses yang mantap dari masukan, penyimpanan, dan pengambilan kembali informasi dalam otak.)" - Johan Japardi
Kelemahan para siswa dalam belajar matematika adalah karena hanya berfokus pada kalkulasi, menghafal rumus tanpa mengamati dari mana datangnya rumus itu, dan mengabaikan konsep dasar karena tidak masuk dalam soal ujian. Jadi mereka bisa dengan mudah mengerjakan soal-soal dengan konsep yang "di tengah-tengah" tapi lupa awalnya. Selain itu, para siswa punya satu kelemahan tambahan: kurang memahami konsep grafik.
Saya sebutkan juga dalam artikel: Berpikir Asosiatif Melihat Keberkelindanan, bahwa pikiran asosiatif diperlukan untuk bisa melihat keberlindanan antar konsep dari pembelajaran-pembelajaran yang berbeda tingkatannya.
Selain kalkulasi, matematika juga harus mencakup aplikasi, sehingga bisa memunculkan inspirasi, dan jika bahan untuk sebuah pembelajaran tidak ditemukan dalam buku, lakukan saja pencarian secara daring.
Contoh: Konsep dasar skala Richter.
Pada 1935, skala kekuatan gempa diciptakan oleh Charles Francis Richter di Institut Teknologi Kalifornia. Saya membayangkan, mungkin dengan pertimbangan agar orang-orang yang mendengar tentang kekuatan gempa tidak panik, maka skala tersebut dibuat logaritmik. Para siswa belajar bahwa bilangan logaritma digunakan untuk mempersingkat penulisan bilangan yang besar, jadi alih-alih 1.000.000, kita tulis log 1.000.000 = log 10⁶ = 6.
Jadi, siswa yang tahu bahwa skala Richter adalah aplikasi bilangan logaritma, dengan mudah menghitung berapa kali lipat kekuatan gempa dari 9 skala Richter dibandingkan dengan 6 skala Richter, yaitu: antilog (9-6) = antilog 3 = 1.000 kali. Apakah sang siswa akan lebih panik dari orang yang tidak mengetahui rumus ini?
Selanjutnya, kita lihat contoh-contoh di bawah ini (semua grafik dibuat dengan perangkat lunak Wolfram Mathematica versi 12.0):
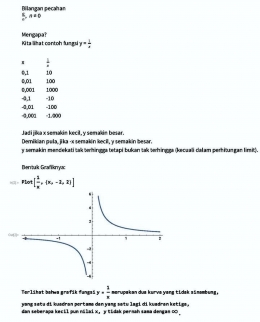
1. Mengapa penyebut bilangan pecahan tidak boleh sama dengan nol? Lihat Gambar-01.
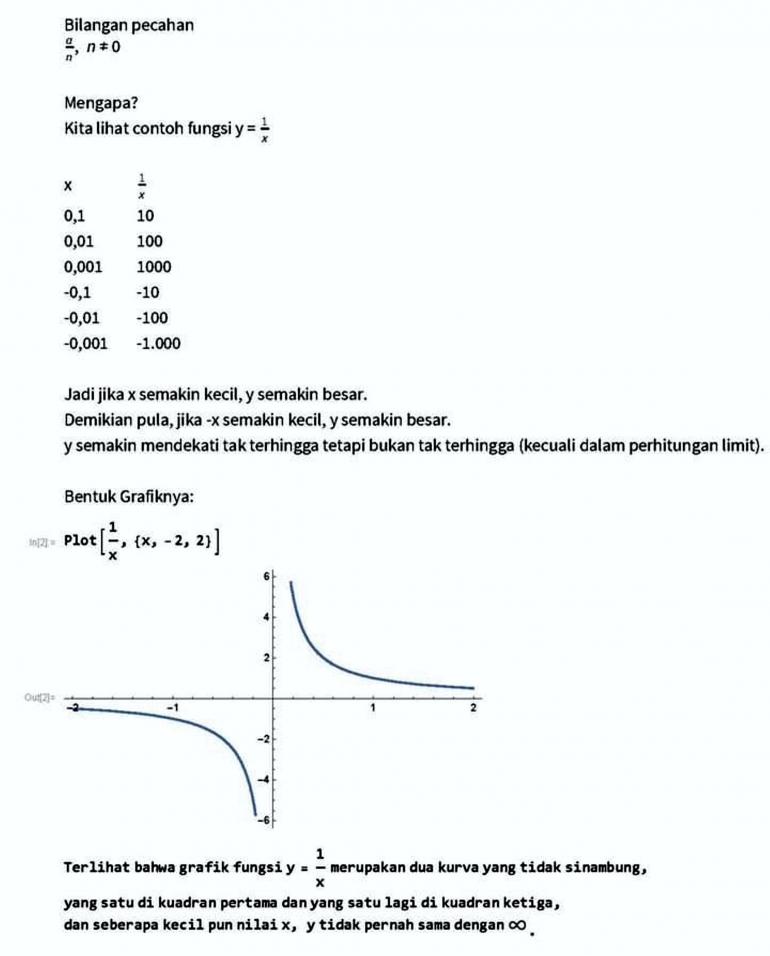
Kesimpulan:
y = 1/x, x ≠ 0.
Untuk x = 0, y tidak didefinisikan karena tak bisa didefinisikan.
2. Kapan penyebut pecahan boleh nol? Jawab: dalam limit.
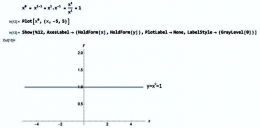
Limit ini sekaligus menjelaskan tentang mengapa turunan dari y = c atau f(x) = c (notasi Newton), yakni y'(x) = 0 atau f'(x) = 0 (notasi Newton) atau dc/dx = 0 atau d/dx (c) = 0 (Notasi Leibniz). Lihat Gambar-02.
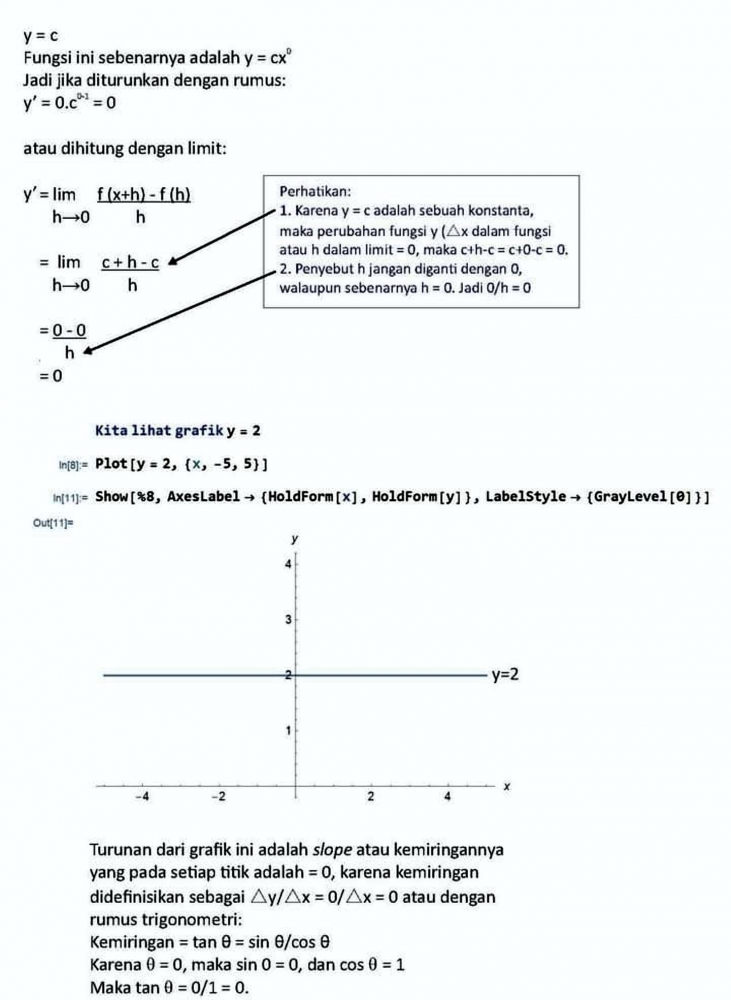
Perhatikan bahwa karena konstanta c adalah bilangan manasuka (arbitrary number), maka kita contohkan saja dengan fungsi y = 2.