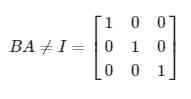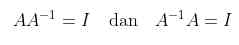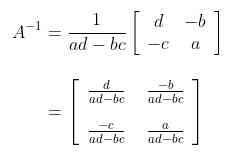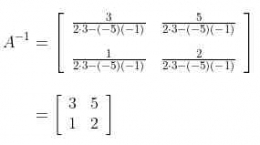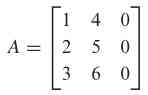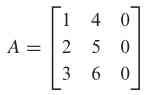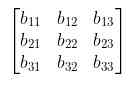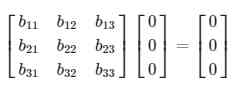Mengenal Sifat-Sifat yang Dimiliki Invers Matriks Beserta Contoh Soalnya!

Jika kamu mendengar kata invers matriks, mungkin kamu akan mengaitkannya dengan fungsi invers, tetapi, sebetulnya kedua istilah ini ini sangatlah berbeda, invers adalah kebalikan atau lawan dari sesuatu. Sedangkan fungsi invers adalah suatu fungsi matematika yang berkebalikan dengan fungsi asalnya. Lalu, apa itu invers matriks?

Invers matriks merupakan suatu matriks baru yang merupakan kebalikan dari matriks asal. Matriks merupakan susunan dengan bentuk persegi panjang atau persegi yang tersusun dari angka-angka dan diatur ke dalam baris ataupun kolom.

Invers matriks sendiri merupakan salah satu metode yang penting dalam menyelesaikan soal-soal dalam sebuah matriks. Sebelum kamu mencari invers dari suatu matriks, maka kamu harus menentukan terlebih dahulu determinannya. Determinan sendiri merupakan suatu nilai yang bisa dihitung dari unsur-unsur matriks persegi.

Invers sendiri bisa diartikan sebagai kebalikan (invers) dari kedua matriks. Jika matriks tersebut dikalikan, maka akan menghasilkan matriks persegi (AB = BA -- I). Simbol dari invers matriks yaitu pangkat -1 dan letaknya berada pada atas hurufnya.

Sebagai contoh, matriks B adalah invers dari matriks A, sehingga ditulis dengan B = A-1 dan matriks A adalah invers dari matriks B yang ditulis A = B-1. Matriks A dan B adalah dua matriks yang saling invers atau saling berkebalikan. invers matriks sendiri terdiri dari dua jenis, yaitu matriks persegi (2x2) dan matriks 3x3.

Sifat-sifat Invers Matriks

Misalnya, terdapat matriks A yang memiliki ordo n x n dengan n N, dan determinan dari A tidak sama dengan nol, jika A-1 adalah invers dari A maka (A-1)-1 = A.

Misalnya, matriks A dan B memiliki ordo n x n dengan n N dan determinannya A dan B tidak sama dengan nol. Jika A-1 dan B-1 merupakan invers dari matriks A dan matriks B, maka (AB)-1= B-1 A-1.

Contoh soal 1: Invers Matriks

Jika terdapat dua matriks

Dok. pribadi

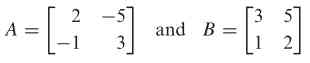
Perkalian dari dua matriks tersebut akan menghasilkan matriks identitas, yaitu sebagai berikut:

Dok. pribadi

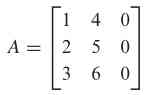
Dengan begitu, maka bisa kita dikatakan bahwa matriks \(A\) dapat dibalik dan \(B\) adalah invers dari \(A\).

Contoh soal 2: Invers Matriks

Jika terdapat matriks

Dok. pribadi

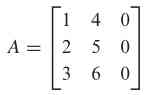
Tidak dapat dibalik. Untuk melihat mengapa demikian, misalkan saja matriks B berikut ini

Dok. pribadi

Adalah sebaran matriks \(3x3\). Kolom ketiga dari matriks BA bisa dihitung dengan:

Dok. pribadi

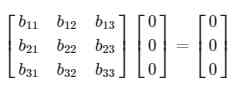
Menjadi,

Dok. pribadi

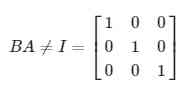
Selain itu, kita juga bisa mengetahui bahwa matriks memiliki baris atau kolom yang semua elemen pada baris atau kolom itu berisikan bilangan nol akan memiliki determinan yang memiliki nilai nol dan karena itu, matriks tersebut tidak bisa dibalik atau tidak memiliki invers.

Pertanyaan yang selanjutnya muncul adalah apakah matriks yang bisa dibalik bisa memiliki lebih dari satu invers. Teorema berikut akan memperlihatkan bahwa jawabannya adalah tidak. Matriks yang bisa dibalik memiliki persisi satu invers saja.

Teorema 1: apabila baik B ataupun C adalah invers matriks A, maka B = C.

Jika A bisa dibalik, maka inversnya dinyatakan dengan simbol \(A^{-1}\). Jadi

Dok. pribadi

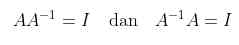
Untuk mencari invers matriks berukuran 2x2, bisa kita gunakan rumus berikut ini.

Dok. pribadi

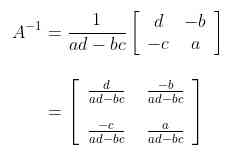
Jadi, invers dari matriks \(\left( {\begin{array}{rr} 2 & -5 \\ -1 & 3 \\ \end{array} } \right)\) adalah 

Dok. pribadi

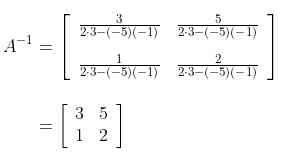
Lalu, perhatikanlah bahwa kitab isa mencari invers dari suatu matriks berukuran \(2x2\) emham sangat mudah. Tetapi bagaimana dengan matriks yang ukurannya lebih tinggi? Maka, rumus di atas tidak bisa banyak membantu.

Teorema 2: jika A dan B merupakan matriks yang bisa dibalik dan memiliki ukuran yang sama, maka

• AB dapat dibalik

• \((AB)^{-1} = B6{-1} A^{-1}\)

Sebuah hasil kali dari matriks yang bisa dibalik selalu bisa dibalik, dan invers hasil kali itu adalah hasil kali invers dalam urutan yang sudah dibalik.

Sifat matriks yang selanjutnya adalah hubungan dengan adjugat. Adjugat dari suatu matriks A bisa digunakan untuk mencari invers dari A, dengan menggunakan hubungan:

Jika A memiliki invers, maka

Dok. pribadi

Itulah sifat-sifat yang dimiliki oleh invers matriks yang bisa kamu pahami dan pelajari lebih lanjut mengenai matriks. Semoga semua pembahasan di atas bermanfaat dan memudahkan kamu dalam mengerjakan soal matriks. 

Penulis: Nurul Ismi Humairoh