Menentukan sudut bouwplank dapat juga memanfaatkan ilmu matematika, yaitu dengan dalil Pythagoras.
Diketahui, teorema Pythagoras digunakan untuk menghitung panjang sisi-sisi dari bidang segitiga siku-siku.
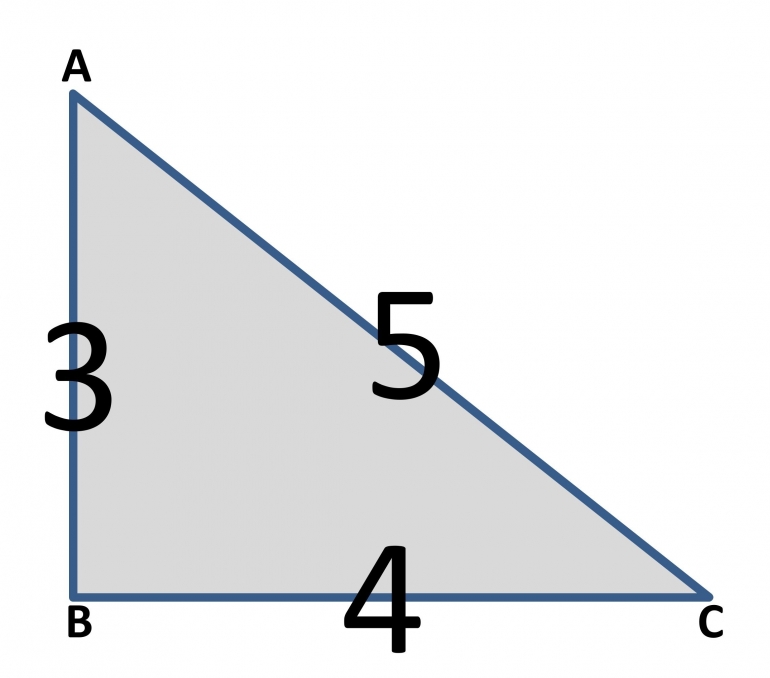
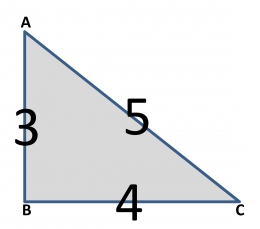
Jika sisi datar dinyatakan sebagai A, sisi tegak dinyatakan sebagai B, dan sisi miring dinyatakan sebagai C, maka akan berlaku persamaan: A kuadrat + B kuadrat = A kuadrat.

Di kalangan tukang bangunan dikenal persamaan gampang-gampangan, yaitu 3-4-5. Artinya: jika 3 satuan pada satu sisi dan 4 satuan di sisi lain, maka sisi miring diukur 5 satuan.
Dengan pola 3-4-5 akan diperoleh sudut yang dapat dipastikan menyiku. Padanannya adalah: 30-40-50; 6-8-10; 9-12-15; 12-16-20; dan seterusnya.
Contoh pengaplikasian pola 3-4-5 adalah dengan cara: mengukur satu sisi 60 cm, sisi lain 80 cm, maka sisi miring berukuran 100 cm.
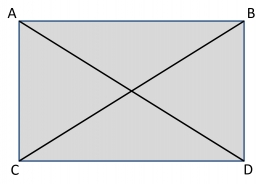
Sesudah sudut-sudut tarikan benang pada bouwplank telah menyiku, tidak ada salahnya mengontrol pengukuran bangunan (atau bagiannya) yang berbentuk persegi empat dengan menggunakan metode berikut.
Tiap sudut masing-masing dinamakan titik A, B, C, dan D. Ukuran diagonal AD seharusnya sama dengan ukuran diagonal BC. Bila tidak sama, dapat dipastikan ada sudut yang tidak menyiku 90.

Bisa jadi sisi AC tidak sama panjang dengan sisi BD. Sisi AB tidak sama dengan CD. Mungkin sisi tersebut tidak sejajar satu sama lain, sehingga bangunan akan tampak mencong.