Matematika Syarat Belajar Filsafat

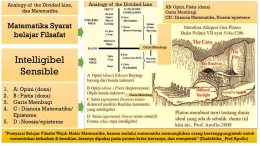
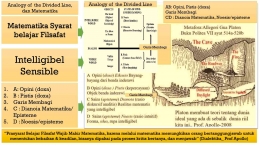
Platon, pada tema  Alegori Gua dan analogi Mataharinya, muncul bersamaan di bagian tengah Republik dan bisa dibilang mengungkapkan pesan inti dari karya filosofis paling penting tentang matematika (lihat gambar).  Seperti yang dijelaskan Platon dalam Buku 7 (7.532e ff.), melalui dialektika kita bangkit dari gua ketidaktahuan menuju noesis. Dengan dialektika, mata jiwa, yang, seperti dalam mitos Orphic, terkubur dalam lumpur, dengan bantuannya yang lembut diangkat pada gambar di atas (7.533cd). 

Bagi Platon, dialektika lebih dari sekedar analisis logis. Ini adalah pemusatan perhatian dan niat seseorang pada pencarian dan hubungan kembali dengan Kebenaran. Hal ini bertepatan dengan penolakan kenikmatan indria sebagai prinsip pengorganisasian kehidupan pikiran seseorang. Dalam arti luas, dialektika dapat mencakup aktivitas apa pun yang melalui pengerahan kecerdasan dan kemauan seseorang, akan terjadi ketajaman mental yang lebih besar. 

Platon sepertinya menyarankan kemampuan mental ini dapat ditingkatkan dengan mempelajari matematika (dan juga musik, senam, dan astronomi  atau apa pun yang menjadi alegori dalam Buku 7). Dialektika adalah topik yang sangat penting bagi Plato, dan dia juga membahasnya dalam dialog-dialognya yang lain (misalnya, Meno, Parmenides, Phaedo, Phaedrus, Philebus, Sophist, Statesman, dan Theaetetus). 

Teknik khusus Platon/Socrates untuk kategori Proclus yang kedua mencakup pengumpulan (mengumpulkan contoh-contoh serupa), pembagian (mencari prinsip-prinsip yang membedakan beberapa contoh dari contoh lainnya), dan metode hipotesis (menjelajahi implikasi hipotesis).  Perhatikan   upaya untuk mendefinisikan dialektika dan menemukan esensinya adalah salah satu bentuk dialektika. Dalam dialognya Platon menyajikan tiga metode pendakian menuju Kebaikan. Di Republik terjadi peningkatan dialektika. Dalam Simposium tersebut terdapat pendakian yang terkenal dengan Love of Beauty. Phaedrus , khususnya dalam Chariot Allegory (metafora kuda putih hitam dan kusir), menggambarkan pendakian dengan Kebajikan Moral (harmonia). Ketiga metode ini pertama-tama naik ke tingkatan Bentuk tertinggi kedua : Kebenaran, Keindahan, dan Keadilan. Seseorang kemudian dapat naik lebih tinggi ke esensi umum mereka, Bentuk Kebaikan, atau Kebaikan itu sendiri.

Mengingat pertanyaan terbuka dalam filsafat alam, Kant membahas hubungan antara matematika dan filsafat. Apakah dunia mempunyai permulaan yang bersifat sementara dan kausal;  Apakah ia mempunyai tujuan spasial;  Apakah materi terdiri dari unsur-unsur penyusun yang sangat kecil;  Apakah ada kebutuhan di alam;  Kant melihat dengan jelas  filsafat alam dogmatis dan populer yang berlaku menegaskan adanya batasan dan keharusan dalam segala hal. Namun, dia tidak dapat membayangkan betapa besarnya kemenangan yang akan diraihnya di bawah panji-panji materialisme dan anti-metafisika. 

Saat ini telah sampai pada titik di mana dikatakan berapa tahun telah berlalu sejak permulaan dunia dan berapa kilometer diameter dunia. Semua partikel elementer dianggap sebagai kombinasi 6 quark, yang berat, diameter, dll diukur. Dalam teori evolusi, asal mula seluruh bagian alam diatur dalam satu rangkaian waktu dan dipostulatkan dengan kebutuhan yang kurang lebih. Kesimpulan logisnya adalah epistemologi evolusioner, yang menyatakan  titik akhir evolusi adalah pengetahuan diri sendiri dalam bentuk ilmu-ilmu alam modern. Ada sesuatu yang tidak beres.

Kant ingin menghindari jalur dogmatis dan  jalur empirisme yang berlawanan, yang menyangkal keberadaan hukum alam dan membatasi dirinya pada analisis individu yang jumlahnya tak terhingga. Dia melihat dua kemungkinan jalan keluar dalam matematika dan filsafat. Matematika merasa lebih mudah dan pada awalnya lebih berhasil.

Ia tidak terlalu menentang dogmatisme dan empirisme karena ia dapat dibimbing oleh persepsi langsung. Tanpa mengkaji sifat-sifat konkrit, tangan dengan lima jari saja sudah cukup untuk berhitung sebagai suatu gagasan dan untuk geometri pandangan bangun-bangun sederhana seperti segitiga, lingkaran, dan lain-lain. Kemudian dibatasi sepenuhnya pada konstruksi konsep-konsep ukuran, seperti nilai numerik, luas, panjang, sudut, dll. Hal ini tidak membuatnya bersifat empiris, karena semua hasilnya valid secara universal,  tidak bersifat dogmatis, karena tidak membuat asumsi yang membatasi mengenai konsep ukurannya. Namun, dengan menggunakan metode konstruksi aritmatika dan geometri yang ketat, ia berulang kali mencapai wawasan mengejutkan yang tidak dapat diharapkan, apalagi dibuktikan oleh filsuf mana pun, hanya melalui pemikiran.

Meskipun demikian, ketertarikan Kant terhadap matematika telah hilang. Secara historis, ia mengikuti pemahaman matematika Platonis, yang menurutnya matematika memiliki objek gagasan abadi tentang objek geometris murni, tetapi tidak dapat melepaskan diri darinya. Terlepas dari semua keberhasilannya, kini ilmu pengetahuan membeku dan hanya mampu mengenali permukaan terluar.

Kita mempunyai dua ungkapan: dunia dan alam, yang kadang-kadang bertemu satu sama lain. Yang pertama berarti keseluruhan matematis dari semua fenomena dan totalitas sintesisnya, baik besar maupun kecil, yaitu kemajuannya melalui komposisi dan melalui pembagian. .Persis sama Namun disebut alam sepanjang ia dipandang sebagai satu kesatuan yang dinamis dan tidak melihat pada agregasi dalam ruang atau waktu untuk mewujudkannya sebagai satu kesatuan, melainkan pada kesatuan dalam keberadaan tersebut. dari fenomena tersebut. (Kant, Kritik Akal Budi Murni/ KABM);

Di era postmodernisme dan simulasi, hal ini mungkin berarti matematika. Bahkan di bidang IT, orang hanya berbicara tentang dunia: dunia Unix, dunia PC, dunia IBM, dll. Namun itu tentu saja tidak cukup bagi Kant. Wittgenstein kemudian menyimpulkannya: Kami merasa  meskipun semua pertanyaan ilmiah telah terjawab, masalah kehidupan kita belum tertangani.

Dan Kant mengatakan  matematika akan segera gulung tikar jika mampu memecahkan pertanyaan-pertanyaan besar dalam filsafat alam.

Meskipun matematika nalar berhasil mencapai keberhasilan baru dalam pengetahuan tentang alam tanpa dogmatisme dan empirisme, namun ia tetap tertahan pada kuantitas belaka. Matematika tetap menjadi teori besaran dan seni pengukuran. Filsafat, sebaliknya, dapat merumuskan gagasan-gagasan luhur, namun ketika menyelesaikannya ia terjebak dalam dogmatisme, empirisme, atau skeptisisme. Kant melihat jalan keluarnya dalam penggunaan ide-ide filosofis secara regulatif. Filsafat tidak seharusnya mengajarkan seperti apa alam itu. 

Pemerintah tidak boleh mencampuri ilmu pengetahuan alam dari luar dan bertindak seolah-olah mereka dapat memahami alam lebih baik daripada ilmu pengetahuan. Ia  tidak boleh berpura-pura  ia dapat melihat ke dalam inti alam dan mengungkap rahasia terdalamnya, yaitu menciptakan sebuah teologi atau mitologi baru. Hal ini dimaksudkan untuk memberikan pedoman yang dapat digunakan oleh ilmu pengetahuan alam sebagai pedoman. 

Karena orientasi memerlukan ilmu yang non-dogmatis dan non-empiris serta tidak bisa mengandalkan persepsi langsung seperti matematika. Ia tidak boleh tenggelam dalam kelimpahan materi, atau dibatasi oleh gagasan-gagasan dogmatis, atau dibatasi oleh alam. Jika ilmu pengetahuan yang tercerahkan tidak mempunyai kemampuan untuk mengorientasikan diri, atau jika ilmu tersebut kehilangan kemampuan tersebut, maka ilmu pengetahuan tersebut pasti akan terjebak dalam suatu proses yang sama berlebihannya dengan gagasan-gagasan luhur tentang keseluruhan alam, yang meruntuhkan setiap pegangan dan dalam kehidupan. bagi sebagian orang, ujungnya tampak sebagai ilmu pengetahuan alam yang tidak terkekang, sementara bagi sebagian orang yang lain sebagai dialektika pencerahan yang tak terhindarkan.

Namun pada pandangan pertama, orientasinya tampak kontradiktif. Kant merumuskan kontradiksi ini dalam Kritik Penghakiman:  Di satu sisi, ilmu pengetahuan alam harus mencari rantai sebab-akibat di mana-mana, dan di sisi lain, ia harus memperoleh pemahaman teleologis tentang alam. Ada dua pola orientasi yang berbeda dalam model mesin dan organisme. Terlalu mudah untuk menyelesaikan perbedaan ini dengan mengacu pada dua bentuk gerak yang berbeda di alam: mesin pada fisika mekanik, organisme pada biologi. Dalam Panduan Kant untuk Orientasi Anda merujuk pada dua situasi berbeda. 

Penilaian teleologis diperlukan untuk mendapatkan pemahaman mendasar tentang alam. Ini adalah interpretasi dan oleh karena itu tidak dapat diungkapkan dalam hukum alam atau sistem tanda matematika lainnya. Dalam kasus yang paling sederhana, penjelasan teleologis tentang alam didasarkan pada pertanyaan: Bagaimana saya akan berperilaku;  Dalam biologi, tentu saja, hal ini paling jelas terlihat. Saat mengamati makhluk hidup, perilakunya dapat dinilai atau dibandingkan dengan cara manusia bertindak. Baik itu dalam komunikasi semut atau dalam keseimbangan energi tumbuhan. 

Namun pertimbangan teleologis  masuk ke dalam fisika. Misalnya, ketika mempertimbangkan sistem yang stabil secara struktural di mana penyimpangan kecil dikompensasi, atau ketika mempertimbangkan prinsip tindakan, yang menurutnya jalur diambil dengan jumlah gaya yang paling sedikit. Fisika penuh dengan hukum kekekalan dan optimasi. Hukum-hukum ini sendiri bukanlah penjelasan teleologis tentang alam, tetapi diawali dengan interpretasi teleologis seperti keseimbangan, harmoni, konservasi, optimalisasi.

Teleologi bukanlah satu-satunya sumber orientasi, meskipun ia menempati tempat paling penting dalam Kant. Anda tidak hanya perlu bertanya: Bagaimana saya harus bersikap;  Sebaliknya, pencelupan  dapat dilakukan untuk merasakan sejauh mungkin betapa berbedanya perilaku yang terjadi di alam dibandingkan perilaku manusia pada umumnya. Alih-alih teleologi, estetika bisa berfungsi sebagai orientasi. Di alam, hubungan tertentu ditonjolkan karena dianggap indah, luhur, atau sebaliknya mengancam, menakutkan, dan aneh. Dalam semua kasus, orientasi mengarah pada keteraturan, penugasan, dan penataan realitas. Namun ini hanyalah soal penafsiran, hanya sekedar kesadaran akan bagaimana alam mempengaruhi manusia, bahkan jika hasilnya membawa keberhasilan praktis dalam eksperimen atau penerapan industri. Ini bukan tentang mengetahui bentuk: batu itu jatuh seperti itu karena ingin melakukan pekerjaan sesedikit mungkin. 

Ini bukan tentang kemauan Anda sendiri, persepsi Anda sendiri tentang keindahan alam. Tidak ada yang dapat dikatakan tentang hal ini kecuali orang tersebut mengasumsikan fantasi kemahakuasaan,  dalam kesadarannya seluruh alam menjadi sadar akan dirinya sendiri,  tubuhnya adalah organisasi tertinggi dari alam yang mengatur dirinya sendiri, atau  alam hanya ada dalam kesadarannya; tidak mungkin untuk melihat keuntungan apa yang diharapkan dari pernyataan pengetahuan tentang dorongan internal alam. Ini semua tentang orientasi, apa yang menjadi milik di mana, bagian mana yang membentuk peralatan bersama atau organisme bersama, nada mana yang terdengar bagus, dll. 

Satu-satunya asumsi tentang alam adalah  ada dasar obyektif untuk penafsiran ini. Orientasi adalah upaya seseorang untuk mencari jalan keluar dari alam dan hanya berpegang pada bagaimana manusia mengalami alam. Tebing-tebing dialektika Pencerahan tidak akan tercapai sama sekali jika tidak ada upaya untuk melompat keluar dari alam dan menilainya secara keseluruhan dari luar, baik secara mitologis (misalnya melalui mitos penciptaan) maupun melalui gagasan-gagasan luhur filsafat alam.

Orientasi tersebut dapat diikuti dengan representasi alam dalam berbagai sistem tanda. Orientasi dan representasi akan saling mempengaruhi satu sama lain. Dalam seni, kesan estetis dapat dikomposisikan, divisualisasikan, atau diungkapkan. Dalam ilmu pengetahuan alam, hukum dicari untuk observasi yang hubungannya telah diakui dalam orientasi. Dan di sini diperlukan orientasi yang berbeda, yang ingin dijawab oleh Kant dalam Kritik terhadap Nalar Murni (Kritik Akal Budi Murni). Orientasi ini diperlukan, namun tidak berarti jelas atau jelas, seperti yang ditunjukkan oleh sejarah matematika. 

Kaum Phythagoras memulai dari penilaian estetika dalam eksperimen musik mereka (yang kedengarannya bagus jika digabungkan), dan kemudian dipandu oleh gagasan  semua hubungan di alam dapat diungkapkan melalui rasio numerik (dalam hal ini dunia terdiri dari angka). Kant ingin memberikan orientasi yang berbeda. Berawal dari penilaian teleologis, hubungan yang ditemukan dipecah menjadi komponen-komponen individual yang dapat direpresentasikan sebagai hukum alam dalam bentuk rantai sebab akibat. Baginya, waktu adalah orientasi di mana hukum-hukum alam dapat dirumuskan secara matematis.

Hal ini membawa kita pada titik di mana matematika dan filsafat saling bersentuhan dalam filsafat kritis Kant. Melalui orientasi awal, diketahui secara kualitatif koneksi dan hubungan internal mana yang ada di alam. Lalu, soal mencatat hubungan-hubungan ini secara kuantitatif. Dalam kasus paling sederhana, dengan struktur alami yang kaku, pertama-tama cukup menentukan secara kualitatif apa yang termasuk dalam struktur dan apa yang tidak, dan kemudian menggunakan tongkat pengukur, dan tugas matematika adalah menemukan ukuran pengikat untuk pengukuran tersebut. dan tugas-tugas sejenis untuk menyelesaikan bagaimana luas atau volume, kepadatan materi, berat, dll. dapat dihitung dari dimensi eksternal. 

Dalam proses dinamis, waktu ditambahkan dan jam berfungsi sebagai alat ukur. Matematika bekerja pada ruang abstrak dengan 3 sumbu spasial dan 1 sumbu waktu, yang sifat umumnya dikenali terlepas dari proses alam mana yang terwakili di dalamnya. Grid ukuran diperiksa secara kuantitatif murni, independen dari proses alam tertentu. Di sisi lain, dalam ilmu pengetahuan alam, kita mengkaji secara kualitatif proses-proses alam mana saja yang memiliki sifat sehingga proses-proses tersebut dapat direpresentasikan. 

Di satu sisi, orientasi filosofis harus memandu bagaimana sifat-sifat kualitatif dapat ditemukan di alam, dan di sisi lain, orientasi filosofis harus mengenali sifat-sifat apa di alam yang disepakati oleh alam dan dunia matematika, dan oleh karena itu alam dapat direpresentasikan. secara matematis. Bagi kaum Pythagoras ini adalah rasio numerik, bagi Plato itu adalah bangun geometri yang ideal, bagi Kant itu adalah waktu murni (Kritik Akal Budi Murni).

Namun di sini dia terjerat dalam kontradiksi. Orientasi terhadap waktu tidak jelas. Kant menjelaskan 3 mode waktu, yang merupakan konsep dasar ilmu pengetahuan alam: substansi sebagai sesuatu yang dipertahankan dalam waktu; Kausalitas sebagai sesuatu yang mengikuti satu sama lain dalam waktu; Interaksi sebagai sesuatu yang tentu terjadi secara simultan (bersama-sama). Meskipun substansi dan kausalitas terletak pada rangkaian waktu (dapat diubah atau tidak dapat diubah), interaksinya terjadi melintasi waktu. Meskipun diakui sebagai milik waktu, namun tidak mempunyai konsekuensi. Ini harus ditelusuri selangkah demi selangkah.

Pertama (I) Antitesis dari ide-ide luhur filsafat alam berkaitan dengan kontradiksi-kontradiksi pengamatan yang berlebihan dan sekilas terhadap rangkaian waktu ketika diyakini  orang dapat melakukan survei rangkaian waktu secara keseluruhan dan membuat pernyataan tentangnya. Kant dengan tegas mengesampingkan sifat-sifat interaksi. Namun semua ide besar muncul dalam sudut pandang yang sangat berbeda ketika kemungkinan interaksi diperhitungkan. Jika banyak hal yang berbeda terjadi pada waktu yang sama dalam setiap momen waktu, rantai sebab-akibat paling baik dapat menangkap suatu penampang melintang. Biasanya, banyak rantai sebab akibat akan berjalan berdampingan pada saat yang bersamaan. 

Dan terdapat persimpangan dan cabang dimana pembangunan dapat dilanjutkan ke arah yang berbeda. Hukum kausalitas, yang menyatakan  hal-hal tertentu harus mengikuti satu sama lain seiring berjalannya waktu, tetap utuh. Namun hubungan antara kebutuhan dan kebebasan telah diubah posisinya. Dan jika rantai sebab-akibat mempunyai kemungkinan untuk bercabang di masa depan dan di setiap masa kini, hal ini  berlaku pada pandangan sejarah alamiah di masa lalu, dimana setiap keadaan yang dicapai merupakan bagian dari suatu interaksi dan dapat dijelaskan oleh rantai sebab-akibat yang berbeda-beda. mengarah ke sana. Ini menyangkut pertanyaan tentang asal mula segala sesuatu yang bersifat kausal dan temporal.

Jika interaksi diperhitungkan, maka tidak mungkin lagi terjadi perpecahan secara sembarangan. Bahkan agregat seperti segumpal pasir pun tidak bisa dipisahkan secara sembarangan. Pada awalnya, pembelahan menghasilkan gumpalan yang lebih kecil, butiran pasir, dll. Kant memikirkan hal ini. Namun pembelahan berakhir ketika molekul tercapai. Jika suatu molekul dibelah maka tidak tercipta separuh molekul, tetapi pembelahan ini merupakan proses kimia yang menghasilkan molekul dan atom lain dengan sifat kimia yang berbeda, karena pembelahan tersebut memecah sekelompok atom yang berinteraksi satu sama lain. 

Kant membayangkan pembelahan sebagai sebuah proses mekanis, namun hal ini akan mencapai batas ketika bentuk pergerakan materi yang lebih dalam tercapai, dan hal ini terus berlanjut. Quark  akan menjadi perhentian sementara. Oleh karena itu, antitesisnya harus diselesaikan secara berbeda di sini. Mekanika kuantum menemukan masalah ini secara eksperimental.

 Namun, dalam lingkaran Weizsacker, dengan tergesa-gesa disimpulkan  kausalitas dan substansi tidak lagi ada ketika proses acak dan ketidakpastian ditemui di alam, yang pada gilirannya hanya merupakan stasiun perantara dalam proses kognitif. Namun, ketika interaksi diperhitungkan, fenomena-fenomena ini harus dinilai dengan cara yang berbeda, sehingga substansi dan kausalitas tetap mempertahankan signifikansinya.

Kedua (II) Seluruh ruang tentu ada dalam setiap momen waktu, yang oleh karena itu secara konsisten digambarkan oleh Kant sebagai interaksi murni, komunitas murni. Jika ruang murni adalah subjek matematika, maka interaksi harus menjadi hal yang sangat penting. Kant menghindari hal ini dengan membuat objek menghilang di balik prosedur matematika. Baginya, matematika pada akhirnya adalah penghitungan, konstruksi geometris, dan pengukuran. Namun semua ini terjadi selangkah demi selangkah dalam rangkaian waktu. Hasilnya selalu tetap, besaran yang kaku (angka atau gambar). Jika Kant membatasi matematika sedemikian rupa dan tidak melihat bagaimana, misalnya, teladan besarnya, Newton, secara matematis menggambarkan interaksi benda-benda mekanis melalui gravitasi, matematika tidak dapat melakukan persis seperti yang ditugaskan Kant: representasi proses dinamis dalam deret waktu. .

Ketiga (III) Pada Opus postumum gravitasi langsung menjadi pertanyaan inti untuk permasalahan selanjutnya. Apa hubungan antara ruang murni matematika dan ruang nyata tempat terjadinya peristiwa alam;  Jelas sekali, Kant pasti berpikir seperti ini: ruang murni adalah ruang kosong di mana benda-benda alam ditempatkan, yaitu ruang di antara benda-benda alam itu kosong. Kausalitas terjadi melalui kontak ketika setidaknya dua hal bertemu dan berubah. Menurut Newton, gravitasi bekerja melalui ruang kosong. Ini pertama-tama merupakan konfirmasi keberadaan ruang kosong.

 Namun bagi Kant muncul masalah: Gaya tarik menarik Newton melalui ruang kosong. Bagaimana ruang kosong itu sendiri dirasakan, karena gaya tidak dapat ada dengan sendirinya tanpa realitas fisik. (Kant). Kant memutuskan  gaya yang melalui ruang kosong tidak mungkin terjadi dan oleh karena itu ruang kosong tidak ada. Namun hal ini memutuskan hubungan antara realitas dan ruang murni matematika, sebuah pertanyaan yang tidak lagi diajukan Kant.

Alternatifnya adalah ruang yang diisi. Dan di sini Kant berkonsultasi dengan semua proses alam yang menjadi subjek penelitian alam abad pertengahan, seperti pembentukan gelembung, pembentukan tetesan, elastisitas, kristalisasi, kelenturan, kerapuhan, guncangan, porositas, pemadatan, gesekan, afinitas, osilasi gelombang, tekstur, lengkungan. Dia mengakui aliran panas sebagai prinsip pergerakan umum yang melaluinya berbagai bentuk solidifikasi dan cairan tercipta. 

Arus menggantikan rangkaian satu dimensi, yang merupakan hal yang sangat penting. Karena dalam aliran (seperti dalam pembentukan tetesan individu, pembentukan gelembung, patahan, dll.) dipertimbangkan pergerakan temporal dari benda-benda alam yang diperluas secara spasial, yaitu komunitas, dari interaksi yang berkembang seiring waktu. Jika ruang diisi sebagai interaksi murni, maka memang seharusnya demikian. Melalui cahaya dan panas, dunia menjadi satu kesatuan, karena zat-zat tertentu yang mengisi ruang tidak hanya efektif di dalamnya. (ibid., hal. 105) Hal ini sangat erat kaitannya dengan gagasan fisik bidang partikel.

Keempat (IV) Dengan adanya ruang kosong ini  jatuhlah model ilmu pengetahuan alam modern, mesin yang dengannya alam direpresentasikan dan diproses. Perasaan hangat (hidup), dingin (mati). Bukan pula zat, melainkan hanya hubungan kekuatan. Udara, cahaya, panas; listrik positif dan negatif.   Cahaya, panas, listrik, dan aliran saraf adalah kekuatan penggerak yang menghasilkan kehidupan di alam semesta seperti galvanisme.  

Ini semua hanyalah catatan, diselingi antara menu Kant dan tujuan tamasya di Opus postumum, dan terkadang saling bertentangan dari halaman ke halaman (terkadang panas adalah suatu zat, terkadang tidak). Namun kesadaran mulai berkembang  ruang yang dipenuhi panas itu hidup, dapat dirasakan oleh manusia dengan seluruh inderanya (bukan hanya mata), dan  ia tidak bisa menjadi sebuah mesin. Lalu bagaimana kita dapat menjelaskan  pergerakan planet-planet, dalam keseragaman dan keteraturannya, bertindak seperti sebuah mesin, murni mekanis;  Kant memikirkan kembali hubungan antara mesin dan organisme. Benda organik adalah benda yang bertindak sebagai mesin dengan menggunakan kekuatannya sendiri. 

dokpri

Di sini, mesin adalah suatu tubuh di mana berbagai rantai sebab akibat dikoordinasikan satu sama lain secara terencana dan mengarah pada hasil tertentu. Dalam hal ini, setiap makhluk hidup dapat dipandang sebagai mesin yang mengolah makanan. Pertanian selalu memanfaatkan hal ini, bioteknologi harus memanfaatkannya lebih jauh. Pertimbangan-pertimbangan ini mengarahkan Kant langsung ke romantisme alami.

Prinsip bergerak non-materi dalam tubuh organik adalah jiwanya, dan jika seseorang ingin menganggapnya sebagai jiwa dunia, kita dapat berasumsi  ia membangun tubuh dan bahkan tempat tinggalnya (dunia). Dari sini pertanyaan mengapa mekanika angkasa muncul sebagai mesin  terjawab.

Amfibolisme (ambiguitas, t.) konsep refleksi yang berkaitan dengan fisika, karena apa yang dibuat adalah pemikiran apriori secara sintetik sebagai sesuatu yang diberikan.  

Mekanika langit ditemukan sebagai sesuatu yang telah menjadi. Segala sesuatunya menyatu di dalamnya, sehingga ia tampak seperti sebuah mesin, sebagaimana adanya. Sebenarnya, ini telah menjadi sesuatu yang historis di mana alam sebagai tubuh organik telah mengorganisir dirinya dengan cara ini dan terus mengorganisir dirinya sendiri. Alih-alih ruang kosong sebagai interaksi murni, alam mengambil tempat sebagai interaksi nyata, yang selalu berubah dan berkembang. Organisme dan mesin keduanya cocok sebagai ide pemandu dengan mempertimbangkan interaksi yang muncul, merencanakan, mempersiapkan, mengendalikan, atau interaksi itu sendiri, sebagai struktur total kekuatan yang saling terkait.

Hal ini pasti  berdampak pada ruang murni matematika. Kant berasumsi  ruang murni adalah Euclidean dan matematika hanya membangun objek di ruang ini. Sebaliknya, jika ruang diasumsikan terisi, tugas pertama matematika adalah mengenali sifat-sifat umum ruang dan kemudian membangun ruang tersebut. Contoh-contoh sifat kualitatif ruang yang diakui secara matematis diketahui dari perkembangan lebih lanjut mekanika langit, di mana dipelajari apakah ruang itu melengkung, apakah mengembang, dll. Dalam arti tertentu, Kant mempunyai gambaran tentang di mana dia berada. mencari contoh metode pencarian geometri sintetik.

Fakta  garis lurus antara dua titik adalah yang terpendek adalah proposisi sintetik. Karena konsep saya tentang garis lurus tidak memuat apa pun tentang ukuran, tetapi hanya kualitas. Oleh karena itu, konsep terpendek ditambahkan sepenuhnya dan tidak dapat dihilangkan dari konsep melalui pembedahan apa pun Garis lurus dapat ditarik. Oleh karena itu, intuisi harus digunakan di sini. (Kant, Kritik Akal Budi Murni)

Kritik Akal Budi Murni/dokpri

Di sini, sifat kualitatif seluruh ruang Euclidean diakui secara matematis, yaitu kedatarannya, yang membuatnya berbeda secara kualitatif dari ruang lain seperti bola atau alam semesta yang melengkung. Artinya matematika tidak lagi sekedar teori besaran, tetapi  mengkaji sifat-sifat kualitatif. Namun, hal ini tidak berarti  ia terlepas dari filsafat dan sejarah. Lebih jauh lagi, harus ditentukan secara filosofis tempat apa yang ditempati matematika dalam pengetahuan tentang alam dan atas landasan apa matematika itu didasarkan.

Hegel tentang matematika alamAksioma tak terhingga dalam kalkulus diferensial. Bagi Hegel, pencapaian luar biasa dari filsafat terletak pada perancangan metodenya. Dengan itu ia dapat mengorientasikan dirinya ke mana saja dan menyelesaikan masalah apa pun. Hubungan antara matematika dan filsafat menjadi perbandingan metode: di sini aksiomatik, di sana dialektis. Geometri Euclidean menjadi contoh cemerlang keberhasilan metode aksiomatik, dan Hegel dengan tepat mengakuinya dalam semua ilmu alam yang meniru geometri Euclidean, seperti mekanika klasik.

Namun dalam ilmu logika matematika tidak digabungkan dengan geometri. Hegel memberikan status khusus pada kalkulus diferensial. Meskipun aksioma Euclid telah berlaku selama lebih dari 2000 tahun, sistem aksioma untuk kalkulus diferensial belum ditetapkan secara sistematis hingga zaman Hegel dan baru pada abad ke-20.

(a) Pengukuran dan intuisi geometri.  Kalkulus diferensial didahului dengan penyelidikan geometri yang kembali ke pertanyaan tentang mengkuadratkan lingkaran. Kurva lengkung secara sistematis didekati dengan garis singgung lurus dengan tujuan untuk menyatakan lingkaran melalui sistem garis singgung, melalui poligon. Untuk fungsi sederhana seperti y = x, turunannya dapat ditebak menggunakan metode geometri dengan mengukur di banyak titik sehingga kemiringan garis singgung di titik x bernilai 2x.

Transformasi simbolisme tersebut mengatakan  aturan perhitungan aritmatika ditinggalkan dan berlaku aturan baru. Lagrange mengadopsi simbolisme ini. Leibniz merumuskan kalkulus diferensial, yang mendefinisikan bagaimana simbol-simbol ini dapat dihitung tanpa terjadi kontradiksi ketika membaginya dengan nol.

Namun ketika Cauchy menerapkan kalkulus diferensial pada himpunan bilangan lain (bilangan kompleks), menjadi jelas  validitas kalkulus diferensial merupakan properti himpunan bilangan yang derivasinya berlangsung dan karena itu termasuk dalam aksiomatik dari kumpulan angka ini. Misalnya pada himpunan bilangan asli tidak dapat diturunkan karena proses limit tidak mungkin dilakukan jika jarak antara dua bilangan asli yang berdekatan selalu satu. Dalam perkembangan selanjutnya, hal ini mengarah pada konstruksi ruang yang memiliki sifat derivabilitas yang persis seperti ini (ruang yang dinormalisasi). Secara khusus, telah ditunjukkan  mekanika dapat diturunkan dalam ruang Euclidean dan dalam ruang gerak. Sebaliknya, ada ruang bernorma yang bukan Euclidean. 

Gagasan Kant dan Newton  ruang Euclidean, ruang alam, dan ruang di mana deduksi dapat dilakukan adalah identik akhirnya hilang. Metode aksiomatik pada awalnya mempunyai efek pembeda yaitu ruang-ruang yang berbeda dapat dibangun di mana aksioma-aksioma tertentu berlaku dan aksioma-aksioma lainnya tidak, yang kemudian diikuti dengan sifat-sifat ruang yang berbeda pula.

Proses aksiomatisasi sungguh luar biasa. Pada awalnya terdapat operasi matematika yang terkenal (seperti konstruksi geometri dan perhitungan aritmatika), yang dalam keadaan tertentu dapat meninggalkan area yang sebelumnya dicakup oleh aksioma. Hal ini menyebabkan didefinisikannya operasi baru (perhitungan aritmatika dalam kalkulus diferensial) yang tidak menerapkan aksioma yang dilanggar. Dan dari operasi baru tersebut, kesimpulan ditarik kembali ke aksiomatik kumpulan angka dan ini diperluas hingga mencakup aksioma yang memperbolehkan operasi baru.

Dalam bentuk akhirnya, sistem aksiomatik terdiri dari definisi yang menentukan himpunan bilangan atau titik, aksioma yang menangkap sifat dasarnya, dan operasi tentang cara membangun himpunan tersebut. Selama ini selalu terbukti adanya ketegangan antara definisi dan aksioma di satu sisi dan operasi di sisi lain. Entah karena tidak jelasnya operasi mana yang sebenarnya mungkin dilakukan (misalnya dalam geometri Euclidean pertanyaan apakah lingkaran dapat dikuadratkan), atau, seperti halnya derivasi, operasi tersebut melampaui cakupan aksioma.

Metode dialektis. Dalam arti tertentu, kita sudah berada di tengah-tengah metode dialektika, di mana sesuatu seperti dialektika aksiomatik telah dibuktikan. Metode aksiomatik berulang kali melampaui batas-batasnya, dan ketika aksioma-aksioma baru dicari, pencarian ini sendiri tidak dapat lagi disebut aksiomatik. Namun akibatnya, hal ini kembali mengarah pada aksiomatik baru, dan metode aksiomatik tidak dapat dihapuskan dalam metode dialektika seperti yang diinginkan Hegel. Ini harus dibenarkan.

Hegel merasa mudah untuk mengkritik metode aksiomatik. Aksioma-aksioma tersebut berdiri bersebelahan tanpa adanya hubungan internal yang dapat dikenali; aksioma-aksioma tersebut tidak berasal dari konsep benda (misalnya konsep bilangan atau konsep ruang); ia tampaknya tidak mengetahui konsep tersebut sama sekali. Hegel membuktikan  prinsip-prinsip tersebut mempunyai karakter sintetik, yaitu, prinsip-prinsip tersebut memberikan hasil yang benar-benar baru dibandingkan dengan aksioma-aksioma dan definisi-definisi, namun prinsip-prinsip tersebut tidak dikembangkan dari konsep benda, melainkan hasil dari operasi mekanis dengan aksioma-aksioma tersebut. 

Mengingat dogmatisme ilmu pengetahuan universitas, kritiknya memiliki banyak manfaat. Aksioma dianggap sebagai hukum dasar struktur negara ilmu pengetahuan, dan siapa pun yang meragukannya dianggap bodoh atau penipu. Setiap hubungan dengan realitas dan kerja praktis dikaburkan; ilmu pengetahuan yang otonom dan bebas merasa puas dengan dirinya sendiri dalam lingkaran aksioma-aksiomanya.

Sebenarnya, aksioma biasanya merupakan teorema dari filsafat (kebanyakan dari logika), catat Hegel. Kalkulus diferensial menghasilkan aksioma kelengkapan: Jika proses limit dilakukan, maka limit tersebut ada, dan bilangan-bilangan tersebut lengkap. Dengan berkembangnya kalkulus diferensial, aksioma ini ditegakkan kembali. Tentu saja, bentuk ini tidak pernah ditemukan di mana pun, bahkan dalam filsafat. Namun telah terjadi perdebatan panjang dalam filsafat sejak Aristoteles tentang kontinum dan berbagai konsep ketidakterbatasan. Konsep gerak kontinu ditemukan dalam eksperimen dan observasi fisik. 

Semua ini memungkinkan ahli matematika menemukan aksioma yang cocok untuk kalkulus diferensial. Salah satu aksiomatis paling berpengaruh, Cantor, secara eksplisit merujuk pada perdebatan skolastik tentang konsep ketidakterbatasan. Leibniz dan Newton menempatkan kalkulus diferensial dalam konteks pertimbangan filosofis alam. 

Fakta  aksioma didasarkan pada prinsip-prinsip dalam filsafat tidak dapat dilihat sebagai suatu cacat. Kecuali sains aksiomatik membeku dalam dogmatisme yang sudah mati, maka sains akan tumbuh subur di tengah ketegangan antara operasi ilmiah dan aksioma. Hal ini terus-menerus mendorong kita menuju aksioma baru. Mata kuliah ilmu alam itu sendiri mengakibatkan perlunya memperjelas landasan filosofisnya.

Metode dialektika pada dasarnya tidak berbeda, walaupun arahnya berlawanan. Sebagai contoh, lihat bagaimana Hegel menafsirkan kalkulus diferensial. Dia memiliki ketertarikan yang bermotivasi filosofis terhadap pertanyaan ini untuk memecahkan teka-teki logikanya (Hegel), seperti yang tak terbatas dalam yang terbatas; Kuantitatif berubah menjadi kualitatif. Dia tidak menemukan solusi dalam filsafat - sebaliknya, dia ingin membawa filsafat lebih jauh dalam masalah ini - namun dalam kalkulus diferensial. Pencarian turunan akan menghasilkan kemiringan garis singgung, dan hal ini dinyatakan dengan perbandingan ukuran y/x sisi-sisi pada segitiga kemiringan. Setelah rasio ukuran tertentu ini ditemukan, terjadilah penyeberangan perbatasan yang membawa kualitas baru. Pada proses limit, y dan x diganti dengan simbol baru dy dan dx.

dx, dy bukan lagi kuanta,  tidak dimaksudkan seperti itu, tetapi hanya memiliki makna dalam hubungan mereka, makna hanya sebagai momen . Mereka bukan lagi sesuatu , sesuatu yang dianggap sebagai kuantum, bukan perbedaan yang terbatas; tetapi bukan nol , bukan nol yang tidak dapat ditentukan. Terlepas dari perbandingannya, bilangan-bilangan tersebut adalah nol murni, namun bilangan-bilangan tersebut hanya boleh dianggap sebagai momen rasio, sebagai penentuan koefisien diferensial dx/dy. 

Dalam konsep tak terhingga ini, bilangan kuantum benar-benar diselesaikan menjadi sebuah eksistensi kualitatif; ia dianggap benar-benar tak terbatas; ia tidak hanya dihapuskan sebagai kuantum ini atau itu, namun sebagai kuantum secara umum (Hegel). Hegel secara nyata mereproduksi cara kerja kalkulus diferensial: ia mencoba merepresentasikannya dalam bahasa filsafat. 

Dia sama sekali tidak dapat menggantikannya, filosofinya tidak memberikan turunan apa pun dan tidak mengembangkan lebih lanjut kalkulus diferensial. Namun dia berhasil dalam hal yang tidak berhasil dia lakukan dalam matematika: menyadari hubungan batin berbagai konsep yang digunakan, berbagai operasi, dan hasil-hasilnya. Sebagaimana dituntut Kant dalam filsafat, ia mempunyai efek yang mengorientasikan, yang hasilnya adalah gagasan matematika alam.

Filsafat hanya dapat dimulai dari materi yang diberikan oleh ilmu-ilmu alam. Dia bisa menafsirkannya. Jika berhasil memperjelas koneksi baru dan membuka cakrawala baru bagi ilmu pengetahuan, maka akan mendorong hal tersebut menjadi sebuah program dan terlaksana. Dia tidak bisa melakukannya sendiri. Sama seperti teori aksiomatik yang menuduhnya kekurangan konsep, teori ini  harus mengakui  para filsuf hanya menafsirkan dunia; intinya adalah mengubahnya.

Mirip dengan estetika dan teleologi, dialektika diberi tugas orientasi, dimana pendekatan-pendekatan yang berbeda terhadap alam tidak dapat ditelusuri kembali satu sama lain; akibatnya adalah dogmatisme. Kant dengan tepat melihat  filsafat tidak dapat meniru metode matematika. Hegel melihat pencapaian karakteristik dialektika dalam mendeteksi diferensiasi internal dalam objek pengetahuan dan menentukan kontradiksi internal yang khas. Namun bukan sebagai paradoks kaku seperti Yunani pra-Socrates, melainkan sebagai sumber pergerakan. Kontradiksi ini mengarah pada penghapusan, pada lompatan kualitatif. Dengan cara ini, dialektika bekerja secara analitis, yang membedakan suatu objek, dan secara sintetik, yang mengenali hubungannya dengan kualitas-kualitas lain dalam proses sublasi.

Seperti halnya dalam teleologi, tidak ada gunanya menyajikan penafsiran sebagai sifat alami yang bersifat langsung, yaitu mengatakan  alam bersifat dialektis. Hal ini menimbulkan arus pendek  setiap ilmu yang diperoleh menjadi suci, alam begini dan bukan sebaliknya, sehingga tidak dapat dikembangkan lebih lanjut. Metode tersebut kemudian menghalangi orientasi lebih lanjut dengan temuan awalnya. Mengikuti Hegel dan Engels, hal ini terjadi pada materialisme dialektis. Tiba-tiba dia curiga terhadap setiap temuan ilmiah baru (seperti teori relativitas, teori kuantum, sibernetika) karena tidak cocok dengan sistem. Pada titik tertentu, buku-buku pelajaran mereka menjadi sama membosankan dan membosankannya dengan buku-buku ilmu pengetahuan borjuis yang diperangi. Akibat fatalnya adalah metode dialektika tidak mampu mengembangkan kekuatan orientasinya, sehingga turut menyebabkan krisis fundamental ilmu-ilmu alam di abad ini yang berujung pada pragmatisme.

 Matematika alam. Hegel telah memberikan kontribusi yang signifikan terhadap perkembangan yang tidak diinginkan ini dengan filsafat alamnya. Namun dalam Ilmu Logika terdapat bukti orientasi kemampuan filsafat dengan gagasan matematika alam.

Ketika kuantitas berubah menjadi kualitas, suatu ukuran didefinisikan secara positif. Turunannya digunakan untuk mencari ukuran pergerakan. Secara fisik, momentum didefinisikan sebagai kecepatan dan momentum, dengan turunan ganda sebagai percepatan dan gaya, dan ketika momentum digabungkan dari waktu ke waktu sebagai energi. Ketika matematika sendiri hanya diperkaya oleh aksioma ketidakterbatasan, Hegel mengakui  dunia yang benar-benar baru terbuka bagi matematika dengan kemampuannya menemukan pengukuran.

Berkenaan dengan proporsi absolut, perlu diingat  matematika alam , jika ingin layak menyandang nama ilmu pengetahuan, pada hakikatnya haruslah ilmu tentang ukuran   ilmu yang secara empiris banyak hal yang mungkin, tetapi sebenarnya ilmiah, yaitu Sedikit yang telah dilakukan secara filosofis. Prinsip-prinsip matematika dari filsafat alam - sebagaimana Newton menyebut karyanya - jika mereka ingin memenuhi tujuan ini dalam pengertian yang lebih dalam daripada yang dimiliki oleh dia dan seluruh keluarga filsafat dan sains Baconian, harus memuat sepenuhnya hal-hal yang berbeda untuk memberikan penerangan ke wilayah-wilayah yang masih gelap tetapi sangat layak untuk dipertimbangkan. 

 Merupakan suatu manfaat besar untuk mengetahui angka-angka empiris alam, misalnya jarak planet-planet satu sama lain, tetapi jauh lebih besar pantas untuk menghilangkan kuanta empiris dan mengubahnya menjadi kuanta umum untuk memunculkan determinasi kuantitatif sehingga menjadi momen hukum atau ukuran;  pahala abadi yang, misalnya, diperoleh Galileo sehubungan dengan kejatuhan dan Kepler sehubungan dengan pergerakan benda-benda langit. Mereka telah membuktikan hukum-hukum yang mereka temukan sedemikian rupa sehingga mereka menunjukkan  sejauh mana rincian persepsi sesuai dengan hukum-hukum tersebut. Namun harus diperlukan tingkat pembuktian yang lebih tinggi terhadap hukum-hukum tersebut, yaitu tidak lain adalah  penentuan kuantitatifnya diakui dari kualitas-kualitas atau konsep-konsep tertentu yang berkaitan (misalnya waktu dan ruang).  

Alur pemikirannya jelas didasarkan pada penyajian kalkulus diferensial. (a) Pertama, kemiringan garis singgung individu diukur (menggunakan metode geometris), yang berhubungan dengan pengamatan bilangan empiris individu melalui pengukuran astronomi. (b) Rumus-rumus kemudian ditemukan untuk penurunan fungsi-fungsi tertentu (menggunakan metode aritmatika yang mengarah pada turunan tentatif), yang kira-kira sesuai dengan hukum gerak planet Kepler. (c) Akhirnya, proses limit dan kalkulus diferensial diperkenalkan, dan Hegel mengembangkannya menjadi program matematika alam. Berdasarkan penelitian ilmiah lebih lanjut, dapat didefinisikan dengan lebih tepat.

Sejak karya Poincar, hukum Kepler dalam mekanika langit telah dijelaskan dari sifat kualitatif ruang gerak mekanis. Jika suatu ruang mempunyai sifat garis penghubung terpendek adalah garis lurus, berarti ruang tersebut tidak bertambah dan tidak menyusut. Dalam kondisi ini, gravitasi bekerja sedemikian rupa sehingga hukum Kepler terpenuhi. Jika ruang mempunyai sifat kualitatif yang berbeda, hukum gerak benda  mengambil bentuk yang berbeda.

Mekanika kuantum lebih berada pada keadaan transisi. Sejumlah besar data empiris dan serangkaian hukum telah tersedia, namun pemahaman kualitatif yang tak terbantahkan tentang alam belum ada. Sifat-sifat ruang di mana mekanika kuantum diterapkan dipelajari. Ini adalah pokok bahasan teori medan kuantum dan pengukur kisi. Teori quark adalah solusi yang mungkin.

Teori bencana  mengikuti jalur ini. Awalnya terdapat banyak pengamatan empiris terhadap turbulensi, ketidakteraturan, dan situasi kacau. Baru terlambat untuk menemukan hukum apa pun dalam kekusutan ini. Sejak tahun 1950-an (dan semakin meningkat sejak karya Thom), penelitian telah dilakukan untuk mengkualifikasikan ruang-ruang di mana bencana terjadi, yaitu ruang terlipat, ruang pecah, ruang dengan singularitas (titik di mana aksioma kelengkapan dilanggar: akankah sebuah singularitas titik didekati dalam proses batas, proses batas masuk ke pusaran air dan menabrak ruang dengan sifat yang berbeda secara kualitatif).

Kant mendefinisikan waktu murni dan ruang murni sebagai titik kontak antara ilmu alam kualitatif dan matematika kuantitatif. Jika ruangan penuh, konsepnya tidak lagi berfungsi. Menurut orientasi Hegel, ini adalah proporsi dimana ilmu pengetahuan alam dan matematika bersatu. Pengukurannya dapat ditemukan dalam ilmu pengetahuan alam (seperti kecepatan cahaya sebagai kecepatan pembatas, konstanta Planck, ukuran molekul tempat gerak mekanis berubah menjadi gerak kimia, dll). Masing-masing ukuran ini merupakan tantangan matematis untuk menentukan radius di mana ukuran tersebut efektif dan bagaimana cara menghitungnya. Orientasi ini lebih banyak pada tradisi Phytagorean, yang mencari hubungan numerik yang mengekspresikan harmoni.***