Untuk menentukan nilai lebih bagi pelanggan Toko Kelontongan Meruya Selatan, kita perlu mencari titik keseimbangan (equilibrium point) yang mencerminkan persamaan permintaan dan tingkat harga keseimbangan.
Dalam persamaan permintaan P = 42 - 5Q - Q^2, kita diberikan bahwa tingkat harga keseimbangan adalah 6. Untuk mencari nilai lebih bagi pelanggan, kita harus mencari nilai kuantitas (Q) pada tingkat harga ini.
Dalam persamaan permintaan, tingkat harga (P) adalah 6, sehingga kita dapat menggantikan P dengan 6:
6 = 42 - 5Q - Q^2
Memindahkan semua suku ke satu sisi, kita dapat menyusun persamaan kuadrat:
Q^2 + 5Q - 36 = 0
Persamaan ini dapat diselesaikan dengan faktorisasi atau menggunakan rumus kuadrat. Karena persamaan ini tidak dapat difaktorkan secara sederhana, kita akan menggunakan rumus kuadrat:
Q = (-b (b^2 - 4ac)) / (2a)
Dalam persamaan kita, a = 1, b = 5, dan c = -36. Menggantikan nilai ini, kita dapat mencari solusi untuk Q:
Q = (-5 (5^2 - 4 * 1 * -36)) / (2 * 1)
Q = (-5 (25 + 144)) / 2
Q = (-5 169) / 2
Q = (-5 13) / 2
Dua solusi yang mungkin untuk Q adalah:
1. Q = (-5 + 13) / 2 = 8 / 2 = 4
2. Q = (-5 - 13) / 2 = -18 / 2 = -9
Karena kita berbicara tentang kuantitas dan dalam konteks ini kuantitas tidak bisa negatif, kita hanya mempertimbangkan solusi positif Q = 4.
Jadi, pada tingkat harga keseimbangan 6, kuantitas yang diminta oleh pelanggan Toko Kelontongan Meruya Selatan adalah 4.
Untuk menggambarkan bentuk kurva permintaan, kita dapat menggunakan nilai-nilai Q dan P yang kita miliki.
Jika kita memilih beberapa titik untuk Q dan kemudian mencari nilai P yang sesuai, kita dapat membuat tabel seperti berikut:
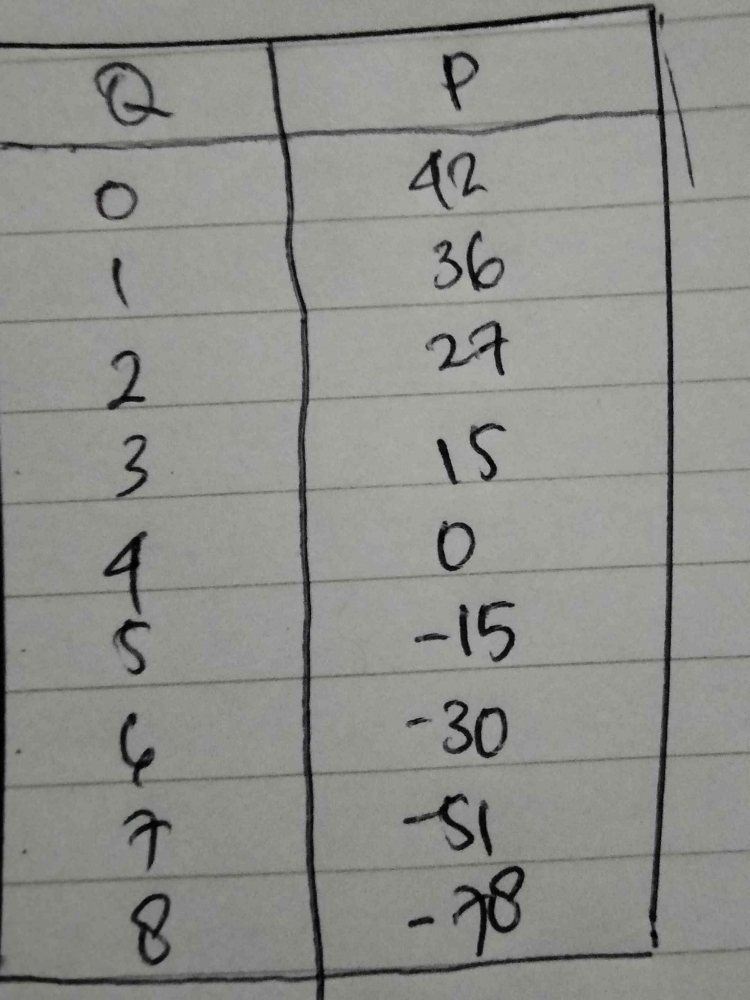
Dengan titik-titik ini, kita dapat menggambarkan kurva permintaan yang menunjukkan hubungan antara tingkat harga (P) dan kuantitas yang diminta (Q).

Untuk menentukan nilai penjualan usaha Caf Sambo, kita perlu menghitung nilai dari persamaan yang diberikan.
Dalam persamaan P = (3-2+1)101, kita diberikan bahwa P adalah harga (price). Dalam hal ini, P adalah hasil dari ekspresi (3-2+1)101.
Kita dapat menghitung nilai P sebagai berikut:
P = (3-2+1)101
P = (2)101
P = 202
Selanjutnya, dalam persamaan Q = (--3+2-1)101, kita diberikan bahwa Q adalah jumlah unit penjualan. Dalam hal ini, Q adalah hasil dari ekspresi (--3+2-1)101.
Kita dapat menghitung nilai Q sebagai berikut:
Q = (--3+2-1)101
Q = (3+2-1)101
Q = 4101
Q = 40
Sekarang, kita diminta untuk menentukan nilai dari (3+2+1)P+Q. Menggantikan nilai P = 202 dan Q = 40 ke dalam persamaan tersebut, kita dapat menghitung nilai tersebut:
(3+2+1)P+Q = (3+2+1)(202) + 40
= 6(202) + 40
= 1212 + 40
= 1252
Jadi, nilai (3+2+1)P+Q adalah 1252.
Baca konten-konten menarik Kompasiana langsung dari smartphone kamu. Follow channel WhatsApp Kompasiana sekarang di sini: https://whatsapp.com/channel/0029VaYjYaL4Spk7WflFYJ2H








