Fraktal adalah salah satu konsep matematika yang telah mengubah cara kita memahami dunia di sekitar kita. Diperkenalkan pertama kali oleh Benoit Mandelbrot pada tahun 1975, fraktal adalah pola yang berulang pada berbagai skala, menunjukkan bagaimana keteraturan dapat muncul dari kekacauan. Dengan kata lain, di dalam kerumitan yang tampaknya acak, ada keteraturan yang tersembunyi. Fraktal telah menemukan aplikasi dalam berbagai bidang, mulai dari geometri, pemodelan cuaca, hingga seni dan arsitektur. Artikel ini akan mengeksplorasi bagaimana fraktal mengungkap keteraturan tersembunyi dalam kekacauan di alam dan bagaimana konsep ini telah memengaruhi berbagai aspek kehidupan kita.
Apa Itu Fraktal?
Fraktal adalah objek geometris dengan pola berulang yang dapat dilihat pada berbagai skala. Ini berarti bahwa jika kita memperbesar bagian kecil dari fraktal, pola yang sama akan terlihat pada bagian tersebut, sama seperti pada keseluruhan objek. Sifat ini dikenal sebagai keserupaan diri (self-similarity). Fraktal tidak terbatas pada bentuk dua dimensi atau tiga dimensi saja, melainkan dapat melibatkan dimensi non-integer, yang dikenal sebagai dimensi fraktal. Konsep ini tidak hanya ditemukan di alam, tetapi juga diterapkan dalam teknologi, seni, dan banyak bidang lainnya.
Sejarah Fraktal
Benoit Mandelbrot adalah seorang matematikawan Prancis-Amerika yang lahir pada tahun 1924. Mandelbrot pertama kali memperkenalkan istilah "fraktal" pada tahun 1975, berasal dari kata Latin "fractus," yang berarti "rusak" atau "retak". Sebelum penemuan ini, pola yang rumit dan tidak teratur dalam alam sering dianggap tidak dapat dijelaskan oleh geometri klasik. Mandelbrot melihat bahwa banyak fenomena alam, seperti garis pantai atau awan, menunjukkan pola yang berulang dan kompleks, tetapi tidak dapat dijelaskan dengan menggunakan geometri Euclidean tradisional. Inilah yang memotivasi dia untuk mengembangkan konsep fraktal, yang memungkinkan matematika untuk mendeskripsikan bentuk-bentuk yang tidak teratur namun memiliki pola tertentu.
Dimensi Fraktal
Salah satu konsep paling menarik dalam teori fraktal adalah dimensi fraktal. Berbeda dengan dimensi dalam geometri konvensional yang biasanya adalah bilangan bulat, seperti 1 untuk garis atau 2 untuk bidang, dimensi fraktal bisa merupakan bilangan non-integer. Misalnya, Koch Snowflake adalah salah satu contoh klasik dari fraktal, yang meskipun terlihat seperti objek dua dimensi, sebenarnya memiliki dimensi fraktal yang bernilai antara 1 dan 2. Dimensi ini mengukur kompleksitas sebuah fraktal, menunjukkan seberapa "penuh" suatu objek menempati ruang di sekitarnya. Konsep ini memperluas pemahaman kita tentang geometri dan membantu kita memahami pola-pola yang tampak acak namun memiliki keteraturan.
Fraktal dalam Alam
Fraktal adalah bagian integral dari alam, ditemukan dalam berbagai fenomena yang kita lihat setiap hari. Pola fraktal terlihat di garis pantai, pegunungan, awan, dan bahkan dalam tubuh manusia.
Garis Pantai
Garis pantai adalah contoh klasik fraktal dalam alam. Jika kita memperbesar bagian kecil dari garis pantai, kita akan menemukan bahwa pola dan bentuk yang serupa dengan keseluruhan garis pantai muncul kembali. Ini menunjukkan bahwa garis pantai memiliki sifat keserupaan diri, salah satu ciri khas fraktal. Studi terhadap garis pantai menggunakan konsep fraktal telah membantu ilmuwan memahami fenomena erosi dan dinamika laut yang rumit.
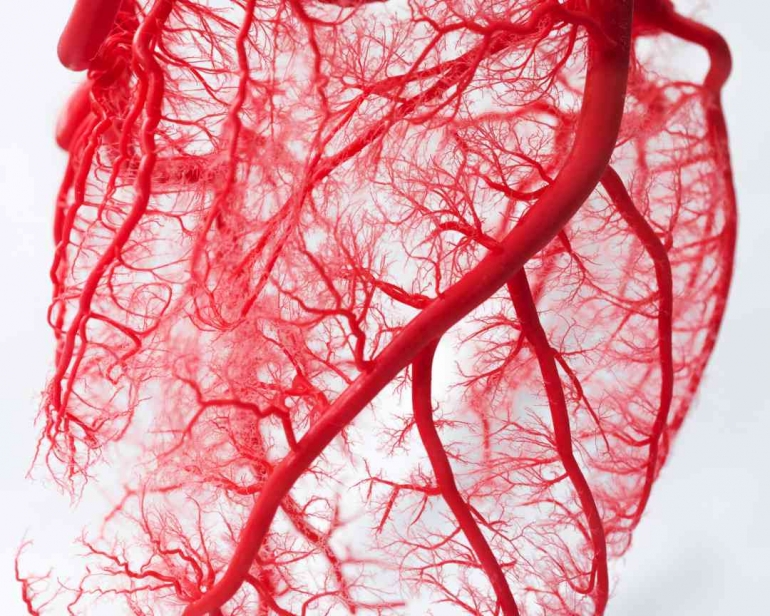
Pembuluh Darah
Di dalam tubuh manusia, sistem pembuluh darah menunjukkan sifat fraktal. Pembuluh darah utama bercabang menjadi pembuluh yang lebih kecil, dan pola ini terus berulang hingga mencapai kapiler terkecil. Pola fraktal ini memungkinkan distribusi darah yang efisien ke seluruh tubuh, memastikan bahwa setiap sel mendapatkan oksigen dan nutrisi yang diperlukan. Penelitian tentang fraktal dalam sistem vaskular juga membuka pintu bagi pengembangan teknologi medis yang lebih baik, seperti pembuatan jaringan buatan.
Awan
Awan juga menunjukkan pola fraktal. Struktur awan yang besar terdiri dari bagian-bagian yang lebih kecil dengan bentuk serupa. Pola ini berulang pada berbagai skala, dari awan besar yang kita lihat di langit hingga partikel kecil yang membentuknya. Studi fraktal pada awan membantu ilmuwan meteorologi memahami pola cuaca dan memprediksi perubahan cuaca dengan lebih akurat.
Aplikasi Fraktal dalam Teknologi
Fraktal tidak hanya ditemukan di alam tetapi juga digunakan dalam berbagai aplikasi teknologi. Konsep fraktal telah membuka jalan bagi inovasi dalam desain antena, pemrosesan gambar, dan banyak lagi.
Desain Antena
Antena fraktal adalah salah satu inovasi yang menggunakan prinsip fraktal untuk meningkatkan efisiensi dan jangkauan sinyal. Desain antena yang kompleks ini memungkinkan penerimaan sinyal yang lebih baik dalam komunikasi nirkabel. Antena fraktal digunakan dalam berbagai aplikasi, mulai dari telepon seluler hingga sistem radar, di mana sinyal yang kuat dan jangkauan yang luas sangat penting.
Pemrosesan Gambar
Dalam pemrosesan gambar, algoritma fraktal digunakan untuk kompresi gambar. Teknik ini memungkinkan penyimpanan gambar dengan ukuran file yang lebih kecil tanpa mengorbankan kualitas. Ini sangat berguna dalam teknologi digital, di mana efisiensi penyimpanan dan transmisi data sangat penting. Dengan menggunakan prinsip fraktal, gambar dapat dikompresi dengan rasio yang tinggi namun tetap mempertahankan detail penting.
Fraktal dalam Seni dan Arsitektur
Fraktal juga telah menginspirasi banyak seniman dan arsitek. Dalam seni, pola fraktal digunakan untuk menciptakan karya yang kompleks dan menarik secara visual. Sementara dalam arsitektur, fraktal diterapkan untuk menciptakan desain bangunan yang estetis dan fungsional.
Seni Fraktal
Seni fraktal adalah bentuk seni yang menggunakan pola fraktal untuk menciptakan karya yang menakjubkan. Seniman menggunakan algoritma fraktal untuk menghasilkan gambar dengan detail yang tak terbatas dan pola yang berulang. Seni ini menciptakan visual yang kompleks dan indah, menunjukkan bagaimana matematika dan seni dapat berkolaborasi untuk menghasilkan karya yang luar biasa.
Arsitektur Fraktal
Dalam arsitektur, konsep fraktal digunakan untuk menciptakan desain bangunan yang unik dan efisien. Pola fraktal dapat meningkatkan efisiensi energi dalam bangunan dan menciptakan ruang yang menarik secara visual. Bangunan dengan desain fraktal tidak hanya indah, tetapi juga fungsional, memanfaatkan ruang dan energi dengan cara yang optimal.
Kesimpulan
Fraktal oleh Benoit Mandelbrot telah mengubah cara kita memahami dunia. Dari mengungkap pola tersembunyi dalam alam hingga menginspirasi inovasi teknologi dan seni, konsep fraktal menunjukkan bagaimana keteraturan dapat muncul dari kekacauan. Dengan memahami fraktal, kita tidak hanya dapat menghargai keindahan alam yang kompleks tetapi juga menemukan cara baru untuk menerapkan prinsip-prinsip ini dalam berbagai bidang. Fraktal adalah bukti bahwa di balik setiap kekacauan, ada pola yang menunggu untuk ditemukan, dan pola ini dapat membawa kita pada inovasi dan pemahaman yang lebih dalam tentang dunia di sekitar kita.
Referensi:
- Fraktal - Wikipedia bahasa Indonesia, ensiklopedia bebas, https://id.wikipedia.org/wiki/Fraktal
- Benoit Mandelbrot - Wikipedia, https://en.wikipedia.org/wiki/Benoit_Mandelbrot
- How Mandelbrot's fractals changed the world - BBC News, https://www.bbc.com/news/magazine-11564766
- The Fractal Geometry of Nature by Benoît B. Mandelbrot | Goodreads, https://goodreads.com/book/show/558059.The_Fractal_Geometry_of_Nature
- Benoit Mandelbrot: Fractals and the art of roughness | TED Talk, https://www.ted.com/talks/benoit_mandelbrot_fractals_and_the_art_of_roughness?subtitle=en
- Benoit Mandelbrot: Fractals and the art of roughness (youtube.com), https://www.youtube.com/watch?v=ay8OMOsf6AQ
- Benoit B. Mandelbrot, MIT 2001 - Fractals in Science, Engineering and Finance (Roughness and Beauty) (youtube.com), https://www.youtube.com/watch?v=ock9Gk_aqw4
- Math's Mysterious Infinite Fractal: The Mandelbrot Set (youtube.com), https://www.youtube.com/watch?v=u9GAnW8xFJY
- Fractals : form, chance, and dimension : Mandelbrot, Benoit B : Free Download, Borrow, and Streaming : Internet Archive, https://archive.org/details/fractalsformchan0000mand
Baca konten-konten menarik Kompasiana langsung dari smartphone kamu. Follow channel WhatsApp Kompasiana sekarang di sini: https://whatsapp.com/channel/0029VaYjYaL4Spk7WflFYJ2H
