"Bagaimana? 1+1 = 1" ?"
Tentu, kita bisa melihat situasi di mana 1+1 tidak selalu menghasilkan 2 dalam konteks probabilitas terapan. Mari kita eksplorasi beberapa kasus:
1. Probabilitas dalam Teori Himpunan:
Misalkan kita memiliki dua kejadian A dan B yang tidak saling lepas (non-mutually exclusive):
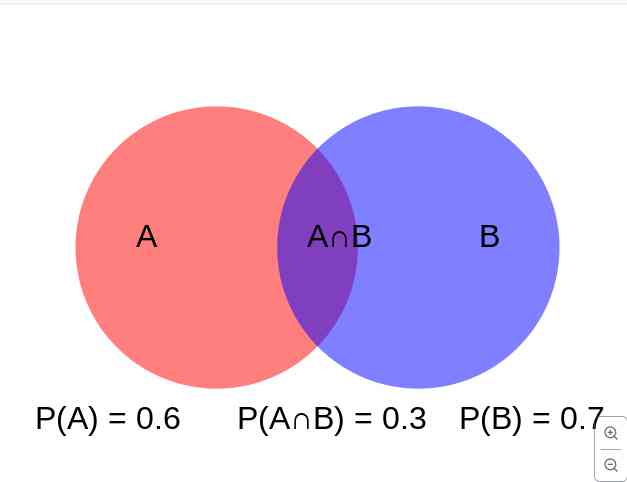
P(A) = 0.6 (probabilitas kejadian A)P(B) = 0.7 (probabilitas kejadian B)
P(AB) = 0.3 (probabilitas irisan A dan B)
Jika kita menjumlahkan probabilitas A dan B secara langsung:
P(A) + P(B) = 0.6 + 0.7 = 1.3
Namun, ini tidak benar karena total probabilitas tidak bisa melebihi 1. Yang benar adalah:
P(AB) = P(A) + P(B) - P(AB)
= 0.6 + 0.7 - 0.3
= 1.0
Dalam kasus ini, 1 + 1 (atau lebih tepatnya 0.6 + 0.7) tidak sama dengan 1.3, melainkan 1.0 setelah memperhitungkan overlap.
2. Logika Fuzzy:
Dalam logika fuzzy, yang menangani ketidakpastian, operasi penjumlahan bisa didefinisikan berbeda:
Misalkan kita menggunakan operator "max" untuk penjumlahan fuzzy:
1 + 1 = max(1, 1) = 1
Di sini, 1 + 1 = 1, bukan 2.
3. Probabilitas Kuantum:
Dalam mekanika kuantum, probabilitas bisa berperilaku aneh. Misalnya, dalam eksperimen celah ganda:
Probabilitas elektron melewati celah 1 = 1/4
Probabilitas elektron melewati celah 2 = 1/4
Namun, probabilitas total bukan 1/4 + 1/4 = 1/2, melainkan bisa mendekati 1 karena interferensi kuantum.
4. Probabilitas Bersyarat:
P(A|B) + P(A|not B) = 1
Di sini, meski kita menjumlahkan dua probabilitas, hasilnya adalah 1, bukan 2.
Kesimpulan:
Meski dalam aritmetika dasar 1 + 1 = 2, dalam konteks probabilitas dan logika lanjutan, penjumlahan tidak selalu bersifat aditif sederhana. Konteks dan aturan spesifik dalam berbagai bidang matematika dan fisika dapat mengubah interpretasi dan hasil dari operasi "penjumlahan" ini.
Follow Instagram @kompasianacom juga Tiktok @kompasiana biar nggak ketinggalan event seru komunitas dan tips dapat cuan dari Kompasiana. Baca juga cerita inspiratif langsung dari smartphone kamu dengan bergabung di WhatsApp Channel Kompasiana di SINI








