Memahami Konsep Faktor Bilangan Prima dengan Mudah
Tahukah kamu bahwa setiap bilangan dapat dipecah menjadi bagian-bagian yang lebih kecil, yaitu faktor-faktornya? Namun, ada faktor-faktor yang sangat istimewa, yang dikenal sebagai faktor bilangan prima. Di artikel ini, kita akan menjelajahi konsep menarik ini dan memahami mengapa faktor bilangan prima begitu penting dalam matematika.
Apa Itu Bilangan Prima?
Bilangan prima adalah bilangan yang hanya memiliki dua faktor, yaitu 1 dan dirinya sendiri. Artinya, bilangan ini tidak bisa dibagi oleh bilangan lain tanpa menyisakan sisa. Contoh dari bilangan prima yang paling umum adalah 2, 3, 5, 7, 11, dan seterusnya.
Menariknya, bilangan 2 adalah satu-satunya bilangan prima genap, sedangkan yang lainnya adalah bilangan ganjil. Semua bilangan lain di luar bilangan prima disebut sebagai bilangan komposit karena bisa dibagi oleh lebih dari dua faktor.
Faktor: Membangun Bilangan dari Dasarnya
Untuk lebih memahami faktor bilangan prima, mari kita tinjau terlebih dahulu apa itu faktor. Faktor adalah bilangan yang dapat membagi suatu bilangan secara habis tanpa menyisakan sisa. Misalnya, faktor dari 12 adalah 1, 2, 3, 4, 6, dan 12 itu sendiri. Namun, dari semua faktor tersebut, hanya bilangan 2 dan 3 yang merupakan bilangan prima.
Nah, disinilah letak keistimewaannya: Faktor bilangan prima adalah bilangan prima yang dapat membagi suatu bilangan komposit. Faktor bilangan prima membantu kita memecah bilangan besar menjadi komponen dasar yang lebih sederhana.
Contoh Menemukan Faktor Bilangan Prima
Mari kita lihat contoh sederhana. Ambil angka 12. Kita tahu bahwa 12 dapat dipecah menjadi faktor-faktor 1, 2, 3, 4, 6, dan 12. Namun, jika kita fokus pada bilangan prima, kita menemukan bahwa hanya 2 dan 3 yang merupakan bilangan prima. Dengan kata lain, faktor prima dari 12 adalah 2 dan 3. Kita bisa menulis 12 sebagai hasil perkalian faktor-faktor prima:
12 = 2 × 2 × 3.
Algoritma Mencari Faktor Bilangan Prima
Berikut adalah algoritma untuk mencari faktor prima dari suatu bilangan:
• Mulai (Start)
• Input bilangan n (bilangan yang akan diperiksa)
• Inisialisasi variabel i dengan nilai 2 (faktor prima terkecil)
• Selama (While) n>1, lakukan langkah berikut:
○ Jika (If) n habis dibagi i (kondisi: n%i==0)
- Cetak i sebagai faktor prima.
- Bagikan n dengan i (setel n=n/i)
○ Jika tidak (Else):
- Tambahkan nilai i dengan 1 (setel i=i+1)
• Ulangi langkah 4 sampai n menjadi 1
• Selesai (End)
Penjelasan:
• Inisialisasi dimulai dengan i=2 karena 2 adalah faktor prima terkecil
• Algoritma memeriksa apakah bilangan n dapat dibagi habis oleh i. Jika Ya, maka i adalah faktor prima dari n, dan n dibagi dengan i untuk menghilangkan faktor tersebut dari n
• Jika n tidak habis dibagi oleh i, nilai i ditambah 1 untuk memeriksa bilangan berikutnya
• Proses ini diulang sampai n menjadi 1, yang berarti semua faktor prima telah ditentukan
Flowchart Mencari Faktor Bilangan Prima
Berikut adalah flowchart untuk mencari faktor prima dari suatu bilangan yang dibuat menggunakan aplikasi Flowgorithm:
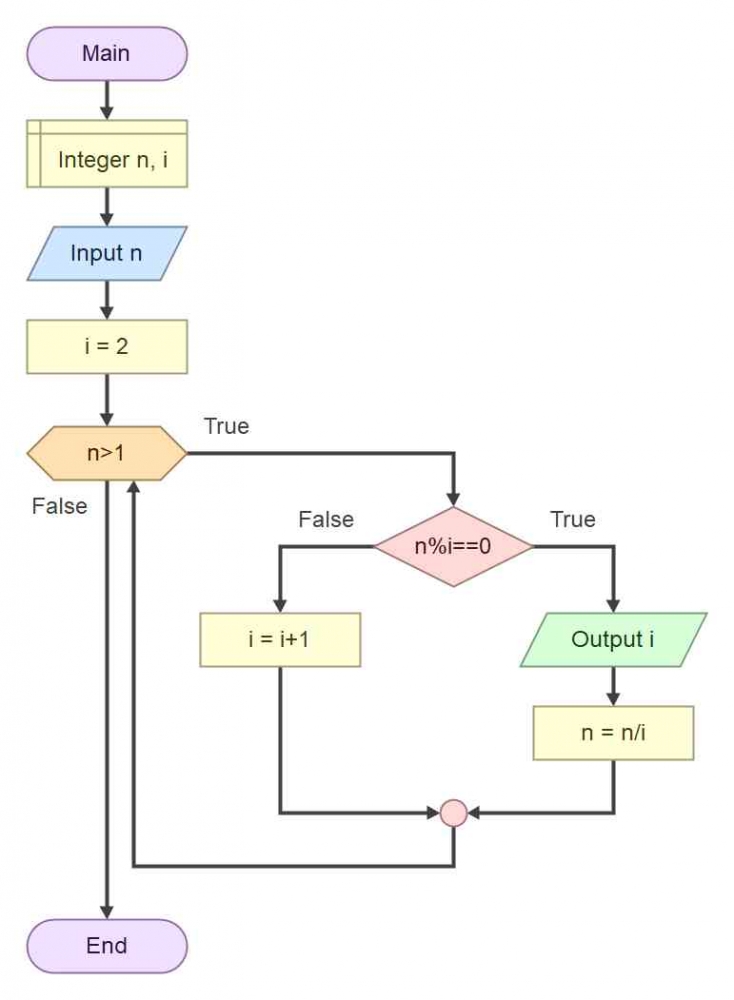
Penjelasan dari setiap langkah dalam flowchart tersebut:
• Main (Mulai): Program dimulai
• Deklarasi Variabel:
○ Variabel n dan i dideklarasikan sebagai bilangan bulat (integer)
○ n adalah bilangan yang akan diperiksa, dan i adalah variabel untuk iterasi, dimulai dari 2 (faktor prima terkecil)
• Input n:
○ Pengguna diminta untuk memasukkan nilai n (bilangan yang ingin dicari faktor primanya)
• Inisialisasi i=2:
○ Variabel i diinisialisasi dengan 2, karena pencarian faktor prima selalu dimulai dari bilangan prima terkecil (yaitu 2)
• Kondisi n>1:
○ Flowchart memeriksa apakah nilai n lebih besar dari 1
○ Jika False (n tidak lebih besar dari 1), program berakhir
○ Jika True, proses dilanjutkan ke langkah berikutnya
• Kondisi n%i==0 (Pemeriksaan Pembagian):
○ Program memeriksa apakah n dapat dibagi habis oleh i (tanpa sisa)
○ Jika True (yaitu n habis dibagi i), maka:
- Faktor prima i dicetak sebagai output
- n dibagi dengan i (nilai n diperbarui menjadi n/i)
○ Jika False (yaitu n tidak habis dibagi i), maka:
- NIlai i dinaikkan sebesar 1 (i=i+1)
• Kembali ke Loop:
○ Proses ini berulang: program memeriksa apakah n masih lebih besar dari 1 dan terus mencoba membagi n dengan i
○ Jika n bisa dibagi habis, n terus dibagi oleh i hingga tidak bisa dibagi lagi
○ Nilai i terus bertambah hingga semua faktor prima ditemukan
• End (Selesai):
○ Ketika nilai n menjadi lebih kecil atau sama dengan 1 ( artinya tidak ada faktor prima lain yang bisa ditemukan), program berhenti
Kesimpulan
Faktor bilangan prima merupakan bilangan-bilangan prima yang dapat membagi suatu bilangan komposit secara habis tanpa sisa. Bilangan prima hanya memiliki dua faktor, yaitu 1 dan dirinya sendiri, sedangkan bilangan komposit memiliki lebih dari dua faktor. Untuk menemukan faktor prima dari suatu bilangan, digunakan algoritma yang memeriksa pembagian bilangan tersebut oleh bilangan prima terkecil (dimulai dari 2), kemudian membaginya secara bertahap hingga semua faktor prima ditemukan. Algoritma ini sangat berguna untuk memecah bilangan besar menjadi komponen-komponen dasar berupa bilangan prima.
Referensi
• ChatGPT
Baca konten-konten menarik Kompasiana langsung dari smartphone kamu. Follow channel WhatsApp Kompasiana sekarang di sini: https://whatsapp.com/channel/0029VaYjYaL4Spk7WflFYJ2H







