Sebuah cara yang efisien, karena untuk mencari suku ke n kita tinggal memasukkan saja nilai n ke dalam rumus dan langsung keluar hasilnya.
Cara yang kedua adalah mengamati gambar dan mencermati polanya.
Untuk soal pertama jumlah noktah tiap suku adalah hasil kali jumlah baris dan jumlah kolom.
Jumlah noktah di tiap suku bisa ditulis sebagai berikut:
Suku ke -1 adalah 1 x 2 = 2
Suku ke -2 adalah 2x 3= 6
Suku ke -3 adalah 3 x 4 = 12
Suku ke -4 adalah 4x 25= 20
Maka suku ke -50 adalah 50 x (50+1) = 2550
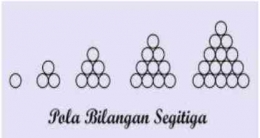
Pada soal kedua jumlah noktah di tiap suku adalah setengah dari jumlah noktah dari soal nomor 1, atau bisa ditulis:
Suku ke -1 adalah 1/2(1 x 2 )= 1
Suku ke -2 adalah 1/2 (2x 3)= 3
Suku ke -3 adalah 1/2(3 x 4) = 6
Suku ke -4 adalah 1/2(4x 5)= 10, maka
Suku ke -50 adalah 1/2(50 x (50+1)) = 1275
Baik menggunakan rumus atau mengamati gambar, akan diperoleh hasil akhir yang sama.
Meskipun menggunakan rumus memerlukan waktu yang lebih cepat, keunggulan dari cara kedua (melihat pola) adalah siswa akan lebih peka terhadap keteraturan sebuah pola. Bisa menemukan keteraturan pola sangat membantu memecahkan masalah, seperti soal nomor 3.
Pada soal nomor tiga untuk mencari angka satuan 2^ 2000 + 3^950, kita tidak perlu mencari hasil dari 2^2000 dan 3^950. Cukup kita cari angka satuan dari 2^2000 dan 3^ 950 dengan menggunakan pola.
Nah, mari kita amati keteraturan bilangan satuan dari hasil perpangkatan berikut:
2 pangkat 1 = 2
2 pangkat 2= 4
2 pangkat 3= 8
2 pangkat 4= 16
2 pangkat 5= 32
2 pangkat 6= 64
2 pangkat 7= 128
2 pangkat 8= 256
2 pangkat 9= 512... dst