Pengertian dan Cara Uji One Way ANOVA dengan SPSS
A. Pengertian ANOVA
ANOVA merupakan metode statistik inferensi yang digunakan untuk menguji rata-rata dari beberapa populasi. ANOVA merupakan perluasan dari uji rata-rata (uji t). Jika uji t menggunakan hanya 2 sampel yang akan dibandingkan, maka dengan ANOVA dapat dibandingkan lebih dari 2 sampel. Karena merupakan perluasan uji rata-rata maka komponen yang digunakan sebagai acuan adalah variansi, sehingga ANOVA disebut juga analisis variansi.
B. Pengertian One Way ANOVA
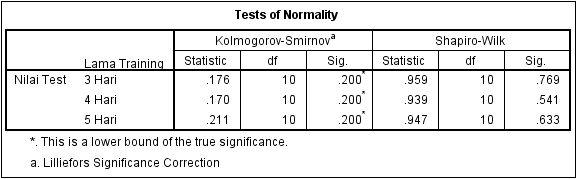
One Way ANOVA adalah uji digunakan untuk mengetahui apakah rata-rata dua atau lebih kelompok berbeda secara nyata atau tidak. Uji One way ANOVA disebut juga uji anova satu faktor. Analisis ini memiliki asumsi bahwa kelompok yang dianalisis memiliki varian yang sama serta data yang digunakan berdistribusi normal
C. Syarat Uji One Way ANOVA
Setiap data yang terkumpul pasti memiliki karakteristik tersendiri, sehingga dibutuhkan metode uji statistik yang tepat. Begitu juga untuk uji One Way ANOVA. Berikut ini persyaratan penggunaan uji One Way ANOVA:
1. Sampel berasal dari kelompok yang indepeden.
2. Variabel faktor (variabel independent) berupa non metrik (data kategorikal).
3. Variabel data penelitian berdistribusi normal.
4. Variabel data penelitian mempunyai varian yang sama (data homogen).
D. Contoh Kasus One Way ANOVA
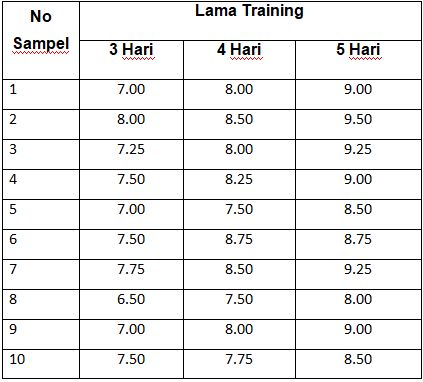
Manajer pemasaran melakukan training untuk para sales. Manajer tersebut menggunakan variasi waktu dalam melakukan training. Ada 3 variasi waktu training yaitu 3 hari, 4 hari dan 5 hari. Manajer ingin mengetahui waktu training manakah yang paling efektif ? Pada setiap sesi training diadakan tes untuk mengetahui peningkatan skill setiap sales. Berikut ini nilai tes para sales selama training:
Baca Juga: Cara Uji Normalitas dengan SPSS
Terkait uji homogenitas dapat dilakukan secara bersamaan dengan uji One Way ANOVA.
E. Langkah-langkah Uji One Way ANOVA dengan SPSS
Berikut ini langkah-langkah uji One Waya ANOVA menggunakan SPSS:
1. Buka software SPSS, langkah awal yaitu melakukan input data di SPSS dengan cara klik Variable View untuk membuat variabel. Pada kolom Name ketik Training pada baris pertama dan Nilai pada baris kedua. Pada kolom label ketik Lama training pada baris pertama dan Nilai training pada baris kedua.
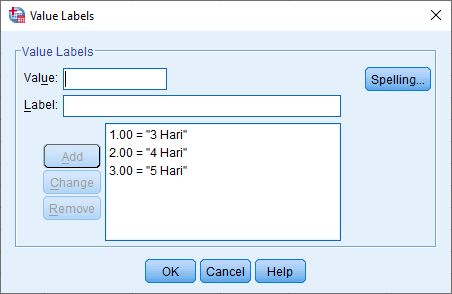
2. Selanjutnya memberi kode pada kolom Values, ketik 1 untuk 3 hari, ketik 2 untuk 4 hari dan ketik 3 untuk 5 hari.

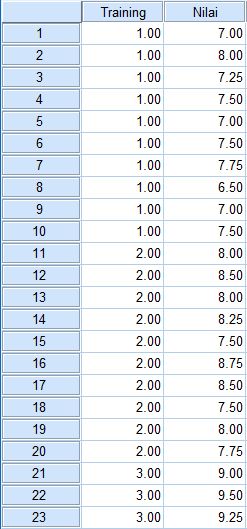
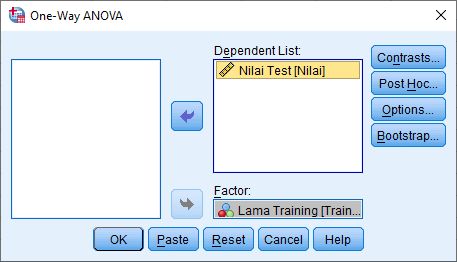
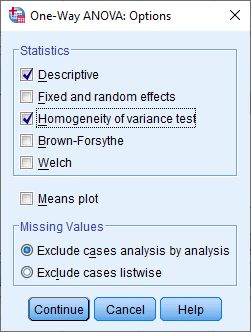
8. Selanjutnya klik OK, sehingga output SPSS menampilkan hasil seperti berikut:
Interpretasi Output Uji Way ANOVA dengan SPSS