Penerapan Aljabar Linear dalam Pengembangan Algoritma Komputer Grafis

Apakah anda tahu apa itu Aljabar Linear ?

Aljabar linear adalah cabang matematika yang mempelajari sistem persamaan linear, seperti peta linear, dan representasinya dalam ruang vektor atau matriks.

Nah, di dalam program studi Teknik Informatika atau Ilmu Komputer mempelajari juga yang namanya Aljabar Linear. Salah satu fungsi Aljabar Linear dalam Komputer yaitu Komputer Grafis.

Computer Graphics (Grafis Komputer) adalah salah satu komponen penunjang komputer yang berkaitan dengan pembuatan dan manipulasi gambar (visual) secara digital. Grafis komputer ditampilkan dalam rupa dua dimensi. Artinya, grafis komputer dua dimensi dan tiga dimensi akan tetap diproyeksikan ke ruang dua dimensi dan ditampilkan ke layar antar muka. Tentu saja grafis komputer tersebut dapat diproses untuk digeser, dapat diperbesar atau diperkecil, dan dapat diputar sesuai dengan kebutuhan dan keinginan penggunanya. Selain perubahan posisi, grafis komputer juga dapat diubah warna dan bentuknya.

A. Matriks dan Operasinya

Matriks adalah susunan bilangan-bilangan berbentuk persegi panjang yang diatur dalam baris atau kolom. Notasi matriks pada umumnya ialah dalam bentuk kumpulan angka menyerupai tabel dan diapit oleh dua buah tanda kurung () atau [].

Berikut ini adalah contoh Matriks.

Matriks pertama berukuran 2x2 yang berarti matriks tersebut memiliki ukuran 2 baris dan 2 kolom. Dengan aturan yang sama, matriks kedua berukuran 1x3 dan matriks ketiga berukuran 3x3. Entri yang berada di matriks A pada baris i dan kolom j dinotasikan dengan aij

Beberapa bentuk khusus matriks antara lain:

* Matriks bujur sangkar adalah matriks yang memiliki banyak baris dan banyak kolom yang sama.

* Matriks segitiga atas adalah matriks bujur sangkar dimana semua entri di bawah diagonal utama bernilai 0.

* Matriks segitiga bawah adalah matriks bujur sangkar dimana semua entri di atas diagonal utama bernilai 0.

* Matriks diagonal ialah matriks bujur sangkar dimana entri pada diagonal utamanya bernilai tidak nol, sedangkan entri lainnya bernilai nol.

 

B. Transformasi Geometri di Ruang Dua Dimensi

Matriks dapat digunakan untuk melakukan transformasi geometri antara lain:

1. Pencerminan (reflection)

2. Perputaran (rotation)

3. Pemampatan (compression)

4. Pengembangan (expansion)

5. Pergeseran (shear)

C. Warna Grafis Komputer

Model warna dasar tersebut dinamakan model RGB (singkatan dari Red, Green, Blue). Model ini dipakai untuk pewarnaan pada monitor komputer.

Masing-masing dari tiga warna tersebut memiliki intesitas saturasi dari 0 hingga 255 (pada representasi bilangan biner, 255 bernilai (11111111)2) sehingga 24 bit sebenarnya ialah kesatuan dari 3 warna dasar tersebut. Nilai 0 menandakan warna dasar tersebut ialah menjadi hitam (#000000), dan nilai 255 menandakan warna asli dari salah satu warna dasar tersebut, misalnya warna merah murni memiliki kode #FF0000. Bila ketiganya dicampurkan pada intensitas saturasi maksimalnya, maka terbentuklah warna putih (#FFFFFF). Berikut menggambarkan pencampuran warna tersebut.

Pencampuran warna RGB/dokpri

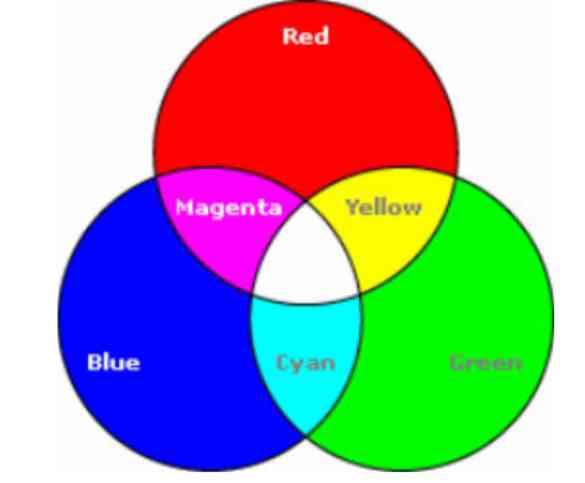
Jadi, Grafis komputer dapat dimanipulasi oleh pengguna komputer itu sendiri. Grafis komputer dapat dipindah tempatnya, diputar, dan diperbesar atau diperkecil melalui penerapan aljabar linier, khususnya matriks. Selain itu, terkait pemrosesan warna, grafis komputer juga dapat diproses warnanya menggunakan penerapan aljabar linier.

Daftar Pustaka

1. Kirana Permata Putri, Ardi Pujiyanta. (2014). Multimedia Pembelajaran Diagonalisasi Matriks. Jurnal Sarjana Teknik Informatika, 2(1), 50.

2. Joshua Atmadja. Penerapan Aljabar Lanjar pada Grafis Komputer. Makalah-IF2123-2015-089.

3. Sumanang Muhtar Gozali. Aljabar Linear. ALJABAR_LINEAR.pdf.

4. Jurnal Teknologi Informasi DINAMIK. 245131-implementasi-sistem-persamaan-linier-men-7917315a.pdf.

5. PENERAPAN ALJABAR LINIER PADA COMPUT. PENERAPAN_ALJABAR_LINIER_PADA_COMPUTER_G.pdf.