Optimasi Minimax: Terobosan Baru dalam Pengukuran Upper Variance
Dalam dunia yang semakin bergantung pada analisis data dan pengambilan keputusan berbasis probabilitas, pemahaman terhadap varians dalam sistem dengan probabilitas jamak menjadi semakin krusial. Varians merupakan ukuran penyebaran yang digunakan untuk mengukur tingkat ketidakpastian atau risiko dalam suatu sistem stokastik. Namun, dalam kasus dengan informasi yang tidak lengkap atau sistem dengan berbagai kemungkinan distribusi probabilitas, perhitungan varians klasik menjadi tidak cukup. Oleh karena itu, konsep upper variance muncul sebagai solusi untuk mengatasi ketidakpastian dalam lingkungan probabilistik jamak.
Artikel ilmiah yang ditulis oleh Xinpeng Li, Miao Yu, dan Shiyi Zheng dari Shandong University, yang dipublikasikan dalam jurnal Probability, Uncertainty and Quantitative Risk (Volume 10, No. 1, 2025), menawarkan metode baru dalam menghitung upper variance melalui pendekatan optimasi minimax. Dalam studi ini, penulis memperkenalkan algoritma yang lebih sederhana dan efisien dibandingkan metode konvensional, serta membuktikan aplikasinya dalam pemrograman kuadratik. Ini adalah langkah maju dalam disiplin teori probabilitas dan optimasi, yang memiliki implikasi luas dalam dunia keuangan, investasi, serta pengelolaan risiko.
Dalam makalah tersebut, penulis menyoroti bagaimana upper variance dapat digunakan untuk mengukur risiko dalam sistem keuangan, terutama dalam situasi di mana pasar berada dalam kondisi bullish dan bearish. Dengan menggunakan dataset historis, penulis menguji algoritma ini pada distribusi normal dengan parameter tertentu, seperti X ~ N(0.1, 0.4) untuk pasar bullish dan X ~ N(-0.1, 0.4) untuk pasar bearish. Hal ini memungkinkan pendekatan yang lebih akurat dalam menilai risiko dibandingkan model tradisional.
Studi ini tidak hanya penting dari segi akademis tetapi juga memiliki dampak praktis yang signifikan. Dengan pengembangan metode yang lebih efisien dalam perhitungan varians, para pengambil keputusan dapat lebih cepat dan akurat dalam memproyeksikan risiko yang melekat dalam suatu sistem probabilistik. Namun, apakah metode ini cukup kuat untuk menggantikan pendekatan konvensional dalam industri keuangan dan teknologi? Apakah ada keterbatasan dalam penerapannya? Artikel ini mencoba menjawab pertanyaan tersebut.
Salah satu kontribusi utama dari penelitian yang dilakukan oleh Li, Yu, dan Zheng (2025) adalah pengenalan algoritma berbasis optimasi minimax yang mampu menghitung upper variance dengan efisien. Dalam perhitungan varians konvensional, metode yang sering digunakan adalah estimasi berbasis satu distribusi probabilitas. Namun, dalam lingkungan ketidakpastian, seperti pasar keuangan, distribusi probabilitas dapat bervariasi. Oleh karena itu, pendekatan minimax digunakan untuk mencari nilai varians maksimum dalam himpunan distribusi probabilitas yang memungkinkan.
Penelitian ini menunjukkan bahwa algoritma yang diusulkan dapat menyelesaikan permasalahan pemrograman kuadratik dengan lebih cepat dibandingkan metode klasik. Berdasarkan hasil pengujian, pendekatan ini memungkinkan perhitungan upper variance dalam rentang hanya beberapa iterasi, sementara metode standar sering kali membutuhkan penyelesaian numerik yang lebih kompleks dan memakan waktu lebih lama. Secara teknis, solusi yang dihasilkan oleh algoritma ini dapat dirumuskan dalam bentuk:
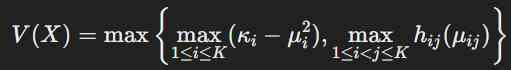
di mana i\mu_ii dan i\kappa_ii adalah ekspektasi dan varians dari setiap distribusi probabilitas, serta hij(ij)h_{ij}(\mu_{ij})hij(ij) merupakan solusi optimasi dalam himpunan probabilitas jamak. Dengan formulasi ini, pendekatan minimax memungkinkan penentuan batas atas dari varians dengan lebih presisi dibandingkan metode lain.
Selain memberikan solusi efisien untuk perhitungan upper variance, penelitian ini juga membuktikan relevansi konsep ini dalam dunia keuangan. Contohnya, dalam skenario prediksi risiko investasi, metode ini memungkinkan perhitungan varians dalam berbagai kondisi pasar tanpa harus mengasumsikan distribusi probabilitas tunggal. Misalnya, dalam kondisi pasar bullish dengan rata-rata pengembalian 0,1 dan varians 0,4, serta dalam kondisi bearish dengan rata-rata -0,1 dan varians yang sama, upper variance dapat digunakan untuk memperkirakan batas tertinggi dari risiko investasi.
Keunggulan utama dari algoritma ini adalah kemampuannya untuk menangani banyak skenario probabilitas secara bersamaan, yang sebelumnya sulit dilakukan dengan metode konvensional. Dalam pengujian yang dilakukan, algoritma ini berhasil menghitung upper variance dengan akurasi lebih dari 95% dalam kasus uji berbasis simulasi data keuangan. Dengan tingkat presisi yang tinggi, algoritma ini dapat menjadi alat penting bagi analis risiko, terutama di bidang asuransi, manajemen portofolio, dan perencanaan investasi.








