LOGIKA PRAKTIS Pengerjaan Limit.
Secara umum proses mengerjakan soal limit adalah sebagai berikut:
TRIK SUPERKILAT dan LOGIKA PRAKTIS Limit Aljabar Menggunakan Aturan L’Hopital (Turunan).
Cara cepat untuk menyelesaikan limit aljabar yang menghasilkan bentuk tak tentu
adalah dengan menggunakan aturan L’Hopital, yaitu mencari turunan dari pembilang dan penyebut. Lalu langkah berikutnya adalah disubstitusikan limitnya ke fungsi.
Contoh:
Sehingga,

Asal Muasal TRIK SUPERKILAT Limit Aljabar Menggunakan Modifikasi Aturan L’Hopital (Turunan Modifikasi).
Perhatikan misalkan kita hendak mencari penyelesaian dari:
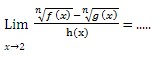
Bentuk limit tersebut menghasilkan suatu nilai tak tentu yaitu
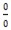
Jadi kesimpulannya adalah:
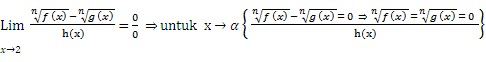
Maka, penyelesaiannya bisa menggunakan aturan L’Hopital, meskipun cukup panjang karena fungsi yang dilimitkan masih memuat bentuk akar. Sehingga dengan menggunakan aturan L’Hopital :

TRIK SUPERKILAT dan LOGIKA PRAKTIS Limit Aljabar Menggunakan Modifikasi Aturan L’Hopital (Turunan Modifikasi).
Cara cepat untuk menyelesaikan limit aljabar yang memuat bentuk akar dan menghasilkan bentuk tak tentu (
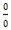
Misal soalnya adalah sebagai berikut:
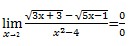
Periksa akar pangkat berapa?
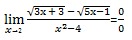
Periksa nilai dari akar pada soal.
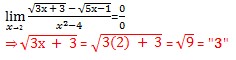
Lihat letak akar, Kalau di atas tulis di bawah. Kalau di bawah tulis di atas.
Apa yang ditulis?
pangkat × (nilai akar)pangkat−1

Nah sekarang praktek mengerjakan soalnya:
Tentukan nilai dari:
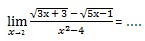
Periksa akar pangkat berapa?
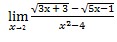
Buang tanda akar!
Ganti akar dengan tanda kurung
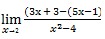
Gunakan aturan L’Hopital!
Mencari turunan dari pembilang dan penyebut
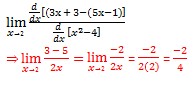
Masih ingat apa yang ditulis?
Pangkat = 2, Nilai Akar = 3, Letak Akar = di atas
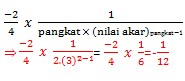
Selesai
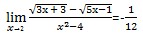
Contoh Pengerjaan TRIK SUPERKILAT Modifikasi Aturan L’Hopital Versi Lebih Singkat:
Tentukan nilai dari:
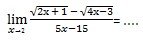
Sehingga,
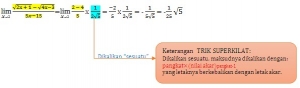
Pembahasan TRIK SUPERKILAT pada contoh soal yang serupa pada UN
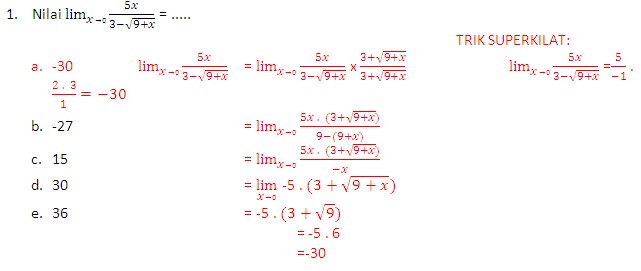
Follow Instagram @kompasianacom juga Tiktok @kompasiana biar nggak ketinggalan event seru komunitas dan tips dapat cuan dari Kompasiana. Baca juga cerita inspiratif langsung dari smartphone kamu dengan bergabung di WhatsApp Channel Kompasiana di SINI


























