Apa itu Golden Ratio (Rasio Emas)? Seperti bisa kita ketahui, Deret Fibonacci bisa kita teruskan hingga tak terbatas. Namun apa yang terjadi bila kita mencari rasio (perbandingan) di antara dua angka di Deret Fibonacci, yakni antara bilangan di depannya dibagi bilangan sebelumnya?
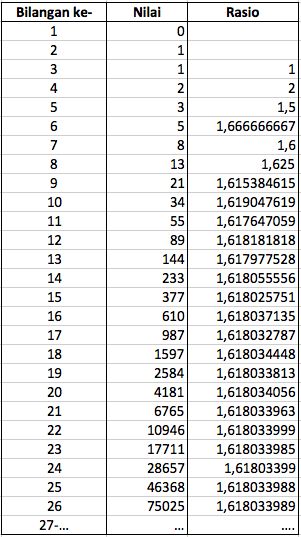
Seperti yang terlihat, angka tersebut akan semakin mendekati nilai 1,6. Angka tersebut dinamakan "Golden Ratio". Apabila terus-menerus dihitung, maka kita akan menemukan nilai "pasti" Golden Ratio tersebut (dilambangkan "phi" atau ) adalah:
= 1,6180339887 ....
Lalu, apa sih keistimewaan Bilangan Fibonacci dan Rasio Emas? Ternyata, banyak struktur di alam dibangun oleh pola-pola yang mengikuti Bilangan Fibonacci dan Rasio Emas. Contoh-contoh yang jelas terlihat adalah pada tumbuhan.
Rasio Emas di Alam
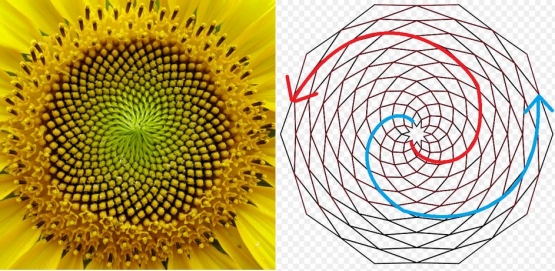
Kita beri contoh bunga. Ternyata bunga tersusun dalam jumlah mahkota bunga yang senilai dengan salah satu Bilangan Fibonacci, semisal berjumlah 1, 2, 3, 5, atau 8. Bahkan bunga-bunga yang terkenal memiliki jumlah mahkota bunga yang banyak (seperti bunga matahari) memiliki jumlah antara 13, 21, 34, sampai 55 yang kesemuanya merupakan Bilangan Fibonacci.

Masih ada lagi, apabila nilai derajat dalam satu lingkaran penuh, yakni 360o dibagi oleh nilai , maka hasilnya adalah 137,51o atau disebut dengan "The Golden Angle" atau "Sudut Emas", Bunga dan biji dalam tanaman (terutama jenis Composit atau bunga majemuk) yang tersusun dalam Sudut Emas ini akan lebih efisien, sehingga akan menampung lebih banyak biji. Biji yang tersusun dalam Sudut Emas ini juga memiliki pola unik yang jika dilihat akan menjelma seperti ilusi optik. Contoh tumbuhan yang memiliki Sudut Emas ini adalah bunga matahari, Chamomile, dan aster.
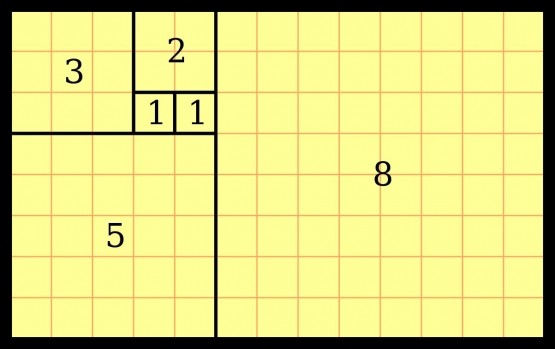
Salah satu ciri khas Bilangan Fibonacci adalah dapat membentuk pola spiral. Misalkan kita membuat satu kotak berukuran 1x1 cm, kemudian di sampingnya kita buat kotak ukuran 1x1 (karena 1 dan 1 adalah dua bilangan pertama Deret Fibonacci). Di bawahnya kita akan bisa membuat kotak berukuran 2x2 (karena 1+1=2). di sampingnya, kita akan bisa membuat kotak berukuran 3x3 (karena 1+2=3), begitu pula seterusnya. Maka akan membentuk sebuah spiral. Spiral ini dapat diteruskan hingga Bilangan Fibonacci di atasnya, bahkan tidak terbatas.