Keterangan :
X= jumlah keluaran
A= matriks masukan
C= matriks permintaan akhir
Jika matriks I -- A bukan matriks singular yakni |I -- A| 0, maka rumusnya adalah
X = (I -- A)-1. C
Untuk mencari jumlah keluaran (X) tersebut harus dihitung melalui beberapa tahap yakni :
1. Menghitung matriks identitas (I) dikurangi matriks A
Karena sudah diketahui koefisien inputnya dan jumlah permintaan akhirnya, maka yang harus dilakukan hanyalah menghitung jumlah keluaran (X). Untuk tahap pertama yang harus dihitung adalah mengurangi matriks Identitas dengan matriks A.

2. Membuat determinan dari matriks Identitas (I) dikurangi matriks A
Cara membuat determinan dari matrisk I dikurangi matriks A sama dengan membuat determinan matriks pada umumnya, maka perhitungan determinan matriksnya adalah sebagai berikut :
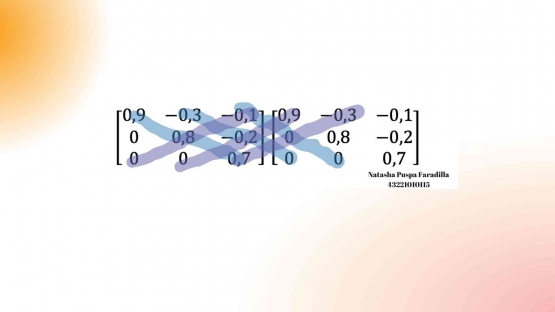
Caranya adalah dengan mengalikan silang secara miring atau serong bilangan matriks. Untuk bagian yang kekanan atau yang ditandai oleh warna biru itu dikalikan kemudian ditambah dengan yang biru lainnya kemudian dikurang oleh perkalian yang ditandai warna ungu yang dikurangi dengan yang lainnya. Sehingga didapatkan kesimpulannya sperti dibawah ini :

3. Mencari add join dengan rumus matriks identitas dikurangi matriks A

4. Mencari jumlah keluaran atau nilai X
Sebelum mencari nilai X, kita terlebih dulu melakukan invers matriks identitas (I) dikurangi dengan matriks A, dengan perhitungannya sebagai berikut :













