Analisis Kesulitan Koneksi Matematis Peserta Didik dalam Menyelesaikan Soal Probabilitas di Sekolah Menengah Atas

Disusun oleh: 1. CINDI APRILIA_34202200012, 2. ERNA EMILIANA_34202200031, 3. ARUM SEKAR ADYOTA_34202200032, 4. MUHAMMAD ADITYA FIRMANSYA _34202200034

Dosen pengampu: Bu Nila Ubaidah, M.Pd. (Dosen FKIP Unissula)

ABSTRAK

Penelitian ini bertujuan mendeskripsikan kemampuan koneksi matematis peserta didik dalam menyelesaikan soal probabilitas yang diperoleh dari peserta didik kelas XII SMA 2 Muara Wahau. Metode penelitian yang digunakan adalah deskriptif kualitatif. Subjek penelitian ini adalah XII SMA 2 Muara Wahau. Teknik pengumpulan data yang digunakan dalam penelitian ini adalah tes dan wawancara. Hasil data menunjukkan bahwa kesalahan yang dilakukan oleh 2 peserta didik dalam mengerjakan soal  materi probabilitas ialah: (1) kesalahan dalam menggunakan konsep kombinasi dan menerapkan rumus, penyebabnya adalah peserta didik tidak dapat memahami maksud soal dan kurang teliti, (2) kesalahan dalam menentukan konsep kombinasi, penyebabnya adalah karena peserta didik kurang paham dan lupa konsep kombinasi karena kesamaan konsep kombinasi dan konsep permutasi, (3) Keselahan dalam menghitung. Guru harus maju, Inisiatifnya untuk meningkatkan pemahaman siswa tentang materi kesempatan belajar.

Kata kunci: kesulitan, peluang, permutasi, analysis, kombinasi, koneksi matematis

PENDAHULUAN

Ada sejumlah kendala yang akan dihadapi peseta didik dalam menyelsaikan permasalahan matematis. (Rahmawati et al., 2017) menjelaskan bahwa beberapa anak merasa sulit untuk membuat koneksi ketika memecahkan masalah matematika, termasuk antara konsep, simbol dan simbol, gambar dan simbol, dan kesalahan koneksi antara cerita kontekstual. Hal senada dikemukakan oleh (Sholekah, Anggreini and Waluyo, 2017) bahwa salah satu tantangan utama yang dihadapi oleh peserta didik ketika mengatasi kesulitan matematika adalah ketidakmampuan peserta didik untuk menghubungkan ide-ide untuk memecahkan masalah. Oleh karena itu, kemampuan mendasar yang diperlukan siswa untuk memecahkan masalah matematika termasuk kapasitas untuk membuat hubungan antara konsep, simbol, dan hubungan antara konsep dan cerita kontekstual.

(Kurniawan, Juliangkary and Pratama, 2019) menjelaskan hubungan antara ide, simbol, dan ide dan masalah terkait konteks sebagai kemampuan koneksi matematis. Penjelasan koneksi matematika juga dikemukakan oleh (Kenedi et al., 2018) bahwa keterkaitan antara ide, konsep, dan metode matematika berkembang sebagai bagian dari jaringan pengetahuan yang saling berhubungan yang terdiri dari konsep-konsep penting untuk dipahami. Hal senada dikatakan oleh (Fatimah and Amam, 2018) bahwa keterkaitan matematika didasarkan pada cara matematika diatur dan terdiri dari potongan-potongan yang terhubung sebagai ilmu.

Karena perkembangan ikatan antara ide, simbol, struktur, dan prosedur, koneksi matematika adalah salah satu variabel mendasar dalam studi matematika dan dapat digunakan untuk mengatasi masalah kontekstual.

(Kusaeri, Pardi and Quddus, 2019) berikut ini adalah contoh koneksi matematis: (1) menyatukan pengetahuan konseptual dan prosedural; (2) menerapkan matematika pada mata pelajaran lain (bidang kurikulum lain); (3) menerapkan matematika dalam kegiatan sehari-hari; (4) memandang matematika sebagai satu kesatuan yang terintegrasi; (5) menggunakan kapasitas untuk berpikir matematis dan mengembangkan model untuk memecahkan masalah dalam pelajaran lain. (6) Memahami hubungan antara tema matematika, dan (7) mengenali berbagai representasi untuk konsep yang sama. Ketika seorang siswa dapat membuat hubungan antara ide, konsep, langkah, dan prinsip-prinsip matematika, pemahaman mereka lebih menyeluruh dan tahan lama, penjelasan koneksi matematis yang dikatakan  oleh (Susanty, 2018). Penjelasan peran koeksi matematis juga dikatakan  oleh (Pambudi, Budayasa and Lukito, 2020) bahwa bakat peserta didik untuk memecahkan masalah matematika akan meningkat dengan meningkatnya keterampilan koneksi matematika. Akibatnya, penguasaan  koneksi matematika akan meningkatkan pemahaman konsep dan mempertajam wawasan matematika, sangat penting bagi peserta didik untuk mengembangkan keterampilan ini sejak usia dini. Hal senada dikatakan oleh (Isnaeni et al., 2018) lebih menyeluruh dan mendalam ketika mereka dapat membuat hubungan antara konsep-konsep matematika.

Salah satu konsep yang dipelajari peserta didik adalah probabilitas. Penjelasan probabilitas dikatakan oleh  (Prihartini, Puspita Sari and Ibnu Hadi, 2020) bahwa menghitung adalah ilmu probabilitas sangat penting untuk mengidentifikasi potensi multiplisitas suatu peristiwa, baik dengan menerapkan metode aturan pengisian tempat atau dengan menyusun semua hasil potensial dalam manual menggunakan diagram pohon, tabel silang, dan pasangan berurutan. Aturan jumlah orang yang hadir tidak hanya memberikan informasi tentang opsi yang tersedia, tetapi juga memungkinkan pengetahuan yang tepat tentang opsi tersebut (terdaftar). Memahami dadu dan koin, yang membantu siswa memahami ide-ide seperti kebebasan dan probabilitas, dapat digunakan dalam permainan dan eksperimen untuk membantu peserta didik mengembangkan pemahaman mereka tentang probabilitas. Probabilitas dan peristiwa tidak dapat hidup berdampingan (Kenedi et al., 2018). Hal ini merupakan upaya untuk meningkatkan standar pendidikan sehingga guru dapat memberikan lingkungan belajar terbaik dan menyiasati masalah yang dimiliki siswa yang menghubungkan pengertian matematika tertentu, dalam hal ini antara konsep matematika. Hasilnya, tujuan penelitian ini adalah untuk mendeskripsikan seberapa baik siswa dapat menghubungkan matematika dengan probabilitas.

METODE

Penelitian ini menggunakan metode kualitatif. Strategi penelitian kualitatif dengan perspektif deskriptif digunakan. (Masyarakat et al., 2018) merumuskan penelitian deskriptif  bertujuan untuk mendeskripsikan apa saja yang terjadi pada saat penelitian sedang dilakukan dan menyelidiki alasan gejala tertentu. Subjek pada penelitian ini adalah 2 peserta didik kelas XII SMA 2 Muara Wahau. Tata cara  penelitian ini terdiri atas tiga tahap, yaitu: 1) tahap persiapan, 2) tahap pelaksanaan, 3) tahap pelaporan.

Langkah-langkah yang dijalankan di tahap persiapan antara lain: (1) Mempersiapkan penelitian dengan membuat pra-pertanyaan yang terhubung secara matematis, (2) Melaksanakan pra riset dengan menyerahkan pertanyaan koneksi matematis kepada peserta didik kelas XII SMA 2 Muara Wahau, (3) Penataan instrument, pedoman penelitian dan wawancara, (4) Memverifikasi akurasi alat penelitian. (5) Memperbarui hasil validasi, (6) Memastikan jawal pnelitian.

Tahap pelaksanaan meliputi: (1) Mengajukan pertanyaan ujian di  15 November 2022, (2) Pada tanggal 4  Desember 2022 akan dilakukan penelitian terhadap dua peserta didik  kelas XII SMA 2 Muara Wahau dan akan diberikan soal berupa tes tertulis, (3) Mendeskripsikan dan mengevaluasi tanggapan siswa dari hasil tes tertulis, (4) Wawancara dengan kedua peserta didik  kemudian akan dilakukan pada 5  Desember 2022, (5) Mendeskripsikan dan mengevaluasi hasil wawancara.

Tahap pelaporan meliputi langkah-langkah sebagai berikut: (1) Mengumpulkan informasi nilai ujian tertulis dan data wawancara, (2) Menganalisis informasi tersebut, (3) Menjelaskan hasil pengolahan data. (4) Menulis makalah penelitian, (5) Sampai pada kesimpulan untuk menyelesaikan masalah.

Teknik pengumpulan data yang digunakan dalam penelitian ini adalah  metode wawancara dan metode pengukuran. Metode pengukuran dalam bentuk instrumen penelitian, seperti esai yang berfungsi sebagai pertanyaan deskripsi pada ujian tertulis (pertanyaan penelitian), dan yang meliputi aturan wawancara. Satu soal penelitian dibuat, dan diujicobakan pada dua peserta didik  kelas XII SMA 2 Muara Wahau.

Memanfaatkan metode tes dan wawancara untuk pengumpulan data. (Zainudin, Utami and Noviana, 2021) menjelaskan bahwa tujuan utama dari tes diagnostik adalah untuk mengidentifikasi kekuatan dan kekurangan peserta didik untuk memberikan bimbingan kepada guru dan peserta didik tentang cara meningkatkan proses belajar mengajar. Peserta didik untuk membuat pilihan yang akan meningkatkan metode pengajaran dan pembelajaran. Sementara wawancara sangat penting untuk mengidentifikasi kesalahpahaman peserta didik karena mereka mungkin mengungkapkan pemahaman menyeluruh tentang individu (Zainudin, Utami and Noviana, 2021).

Pada 5 Desember 2022, wawancara dilakukan satu persatu dengan masing-masing dari dua peserta didik yang telah dipilih. Tujuan wawancara yang tidak terstruktur adalah untuk mendapatkan informasi yang mendalam dan menyeluruh mengenai pendapat siswa (Rahmawati et al., 2017). Selain itu, prosesnya wawancara digunakan untuk menguatkan hasil tes dan memverifikasi tanggapan siswa.

HASIL DAN PEMBAHASAN

Hasil

Setelah peerta didik memiliki kesempatan untuk belajar, tes diberikan kepada mereka. Ada beberapa kesalahan yang dilakukan oleh peserta didik ketika menyelesaikan soal probabilitas berdasarkan hasil belajar siswa. Kesalahan yang dilakukan peserta didik berkisar dari bagaimana cara melakukannya. Soal yang diberikan dapat dilihat di bawah dan jawaban siswa dapat dilihat pada Gambar 2.2 dan Gambar 3.3. 

Soal:

Sebuah kantong berisi 22 buah kelereng yang terdiri dari 13 kelereng putih  9 elereng hijau. Berapakah peluang mengambil 5 kelereng hijau sekaligus?

Gambar 3.3 Jawaban Peserta didik 2

Menurut jawaban peserta didik, jelas bahwa mereka mengalami masalah atau tidak dapat mengatasi masalah praktis probabilitas. Tabel  akan ditampilkan untuk menggambarkan dengan lebih jelas betapa sulitnya hubungan matematis siswa.

screenshot-2022-12-11-204343-6395ded6eb51ce42d13617d2.png

Satu gambar diambil untuk setiap ketidakakuratan dan peserta didik diwawancarai berdasarkan data yang telah dikumpulkan. Berikut adalah jenis kesalahan yang biasanya dilakukan peserta didik saat mencoba menjawab pertanyaan berdasarkan materi probabilitas.

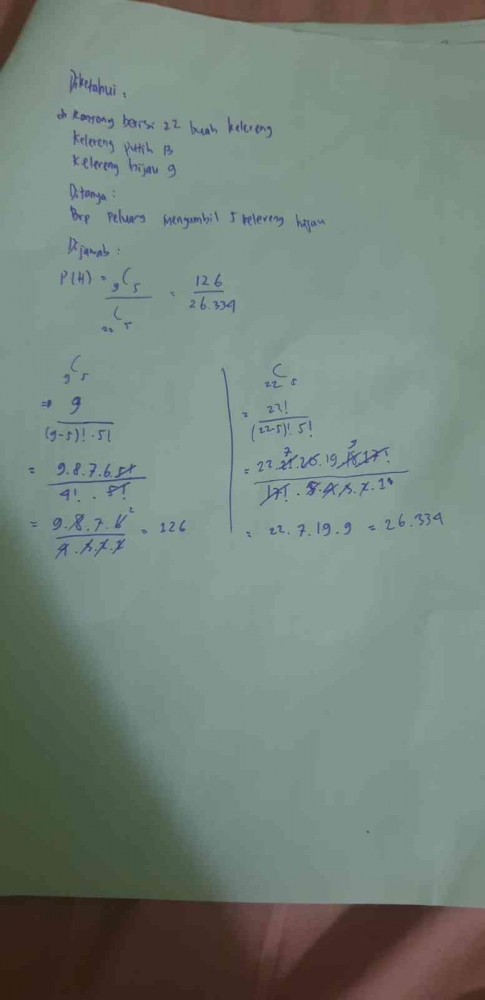
Kesalahan dalam merekam apa yang diketahui, kesalahan dalam memahami pertanyaan, dll.

Materi soal diakui oleh kedua peserta didik . Mereka mampu menentukan apa yang diminta dengan menulis secara akurat berdasarkan apa yang dipahami dan benar.

            Gambar 2.2 dan Gambar 3.3 menunjukkan bahwa siswa mampu mengenali fakta terkait soal probabilitas. Wawancara dengan peserta didik 1 berfungsi untuk mendukung hal ini dan untuk peserta didik 2 tidak dilakukan wawancara karena jawabanya sudah benar. Hasil utama dari wawancara yang dilakukan oleh para peneliti adalah bahwa kedua peserta didik  sudah memahami ide dasar probabilitas. Mereka tidak ragu untuk mencatat informasi masalah secara akurat.

 

Kesalahan dalam menentukan konsep kombinasi 

Salah satu kesalahan yang dilakukan peserta didik 1 yang terkait dengan gagasan kombinasi adalah (1) menggunakan dan menerapkan rumus secara tidak benar, dan (2) salah menentukan kombinasi. Peserta didik 1 memecahkan masalah menggunakan pendekatan permutasi ketika pendekatan kombinasi dapat digunakan. Ini bisa jadi karena peserta didik lupa atau tidak terbiasa dengan rumus tersebut.

Berdasarkan hasil pekerjaan peserta didik 1 pada Gambar 2.2, terlihat bahwa dia menyelesaikan soal dengan menggunakan konsep permutasi. Seharusnya soal tersebut diselesaikan dengan menggunakan konsep kombinasi. Hal ini disebabkan karena lupa. Berikut petikan hasil wawancara dengan peserta didik.

Peneliti : "Saat mengerjakan soal ini, darimana kamu mendapat rumus ini?"

Peserta didik 1: "Saat mengerjakan soal, saya tertujunya pada rumus ini kak. Soalnya menurut saya cocok sama materi dan soal yang ditanyakan."

Peneliti : "Menurut mu yang kamu masukkan dalam pengerjaan soal itu rumus apa?"

Peserta didik 1: "Itu rumus permutasi kak"

Peneliti : "Jadi menurutmu itu tadi soal permutasi?"

Peserta didik 1: "(membaca soal) iya kak, ini bentuk soal permutasi"

Peneliti : "Coba baca soalnya sekali lagi dengan teliti!"

Peserta didik 1: (sambil membaca soal kembali) "Ini bentuk permutasi kak."

Peneliti : itu bentuk kombinasi"

Peserta didik 1: oooh iya, ini bentuk kombinasi. saya salah berarti kak. saya kira itu bentuk permutasi soalnya keduanya hampir mirip"

            Menurut hasil wawancara, kesalahan peserta didik 1 adalah karena lupa karena kedua konsep tersebut identik. Menurut hasil wawancara peserta didik, peserta didik  melakukan kesalahan karena tidak teliti, tidak dapat memahami maksud soal, memasukkan angka ke dalam rumus yang salah, dan "lupa" karena mereka merasa konsep kombinasi dan permutasi adalah sama.

Pembahasan 

Peserta didik umumnya membuat kesalahan dalam pemerolehan informasi, kesalahan konseptual, dan kesalahan kalkulasi ketika berusaha memecahkan masalah matematika yang membutuhkan koneksi matematika. Ketiga kesalahan tersebut juga terjadi dalam penelitian yang dilakukan oleh (Bakhril, Kartonoa and Dewi, 2019);(Nurdin, Nufus and Hasanuddin, 2018);(Nari and Musfika, 2016). Hal ini senada yang dikatakan oleh (Kusaeri, Pardi and Quddus, 2019) tiga komponen utama dari program pengajaran proses koneksi matematika dalam standar adalah: (1) mengenali dan menggunakan hubungan antara ide-ide matematika; (2) memahami bagaimana ide-ide matematika saling berhubungan dan dikonstruksi untuk menghasilkan satu kesatuan yang utuh; dan (3) mengenali dan menerapkan matematika dalam konteks di luar matematika. Akibatnya, dengan berfokus pada indikasi pemahaman informasi, pemahaman konseptual, dan kompetensi operasi matematika, matematika peserta didik dapat ditingkatkan.

Kemampuan peserta didik dalam menggambarkan masalah sebagai simbol matematika atau membangkitkan simbol matematika disebut sebagai pemahaman materi dalam penelitian ini pemodelan matematika adalah istilah yang digunakan untuk menggambarkan ketidakmampuan peserta didik untuk menerjemahkan masalah ke dalam simbol matematika. Hal ini senada dengan penelitian yang dilakukan oleh (Kusaeri, Pardi and Quddus, 2019) menuliskan apa yang diketahui dan apa yang ditanyakan dalam seluruh soal dalam bentuk kata-kata dan simbol matematika (fakta) yang telah dipahami memungkinkan seseorang untuk merekam informasi pemahaman mereka dengan mengaitkannya dengan data dan pertanyaan tentang masalah yang mereka hadapi. mencoba untuk menjawab. Oleh karena itu, aspek penting dari pelajaran matematika yang perlu diperhatikan adalah kemampuan siswa untuk memahami informasi dan menuliskannya dalam simbol.

Indikator pengetahuan konseptual merupakan salah satu hal yang menghambat peserta didik  dalam memecahkan masalah matematika. Menurut data wawancara yang dikumpulkan, pemahaman konsep peserta didik yang buruk adalah akibat dari mereka melupakan dasar konsep. Istilah psikologis untuk kelupaan yang disebabkan oleh kesamaan adalah interferensi. Teori interferensi menurut(Wahidah and Qudsyi, 2011) alasan kehilangan memori adalah kejadian umum yang disebabkan oleh interferensi antara elemen informasi serupa selama fase penyimpanan dan proses mengingat.

Berdasarkan temuan penelitian ini, sangat ideal untuk mengurangi kesalahan informasional, konseptual, dan kalkulasi untuk meningkatkan koneksi matematis peserta didik. Hasil penilitian dilakukan oleh (Siagian, 2016) menjelaskan bagaimana pembelajaran konstruktivisme merupakan salah satu metode pembelajaran yang dapat meningkatkan pemahaman tentang cara menerima informasi, kesalahan yang berkaitan dengan konsep, dan kesalahan menghitung. Untuk membangun koneksi matematis, salah satu metode yang dapat digunakan adalah pembelajaran konstruktivisme. Sebagai yang disebutkan oleh(Hamdani and Nurdin, 2020) bahwa dengan menggunakan pembelajaran strategis siswa secara efektif, hubungan matematis dapat ditingkatkan.

KESIMPULAN

Kesimpulan bahwa peserta didik terus melakukan banyak kesalahan saat menyelesaikan masalah probabilitas dapat disimpulkan dari hasil penelitian dan analisis data yang telah disediakan. Kesalahan ini salah karena gagal memahami ide permutasi dan kombinasi dan mengandung kesalahan matematika. Kesalahan ini dapat dimanfaatkan sebagai alat pengajaran oleh instruktur untuk meningkatkan pengajaran di kelas. Guru harus membantu peserta didik memahami materi probabilitas, khususnya pengertian permutasi dan kombinasi, sehingga mereka dapat membedakan kedua konsep tersebut dan menyelesaikan masalah yang disajikan.

DAFTAR PUSTAKA

Bakhril, M.S., Kartonoa and Dewi (2019) 'Kemampuan Koneksi Matematis Siswa Melalui Model Pembelajaran Peer Tutoring Cooperative Learning', Prisma: Prosiding Seminar Nasional Matematika, 2(ISSN 2613-9189), pp. 754--758. Available at: https://journal.unnes.ac.id/sju/index.php/prisma/ ISSN.

Fatimah, A.T. and Amam, A. (2018) 'Rencana Pelaksanaan Pembelajaran Matematika Di Sekolah Menengah Kejuruan', Jurnal Penelitian dan Pembelajaran Matematika, 11(2). Available at: https://doi.org/10.30870/jppm.v11i2.3756.

Hamdani, M.F. and Nurdin, E. (2020) 'Kemampuan Koneksi Matematis berdasarkan Minat Belajar Siswa', JURING (Journal for Research in Mathematics Learning), 3(3), pp. 275--282. Available at: http://ejournal.uin-suska.ac.id/index.php/juring/article/view/10346.

Isnaeni, S. et al. (2018) 'Analisis Kemampuan Koneksi Matematis Siswa SMP Pada Materi Persamaan dan Pertidaksamaan Linear Satu Variabel', journal On Education, 01(02), pp. 309--316. Available at: https://jonedu.org/index.php/joe/article/view/68/56.

Kenedi, A.K. et al. (2018) 'Kemampuan Koneksi Matematis Siswa Sekolah Dasar dalam Memecahkan Masalah Matematika', Jurnal Numeracy, 5(2), pp. 226--235.

Kurniawan, A., Juliangkary, E. and Pratama, M.Y. (2019) 'Analisis Kesulitan Siswa Dalam Menyelesaikan Soal Fungsi', Media Pendidikan Matematika, 7(1), p. 72. Available at: https://doi.org/10.33394/mpm.v7i1.1679.

Kusaeri, A., Pardi, H.H. and Quddus, A. (2019) 'Culture and mathematics learning: Identifying students' mathematics connection', Beta: Jurnal Tadris Matematika, 12(1), pp. 82--93. Available at: https://doi.org/10.20414/betajtm.v12i1.264.

Masyarakat, P. et al. (2018) 'Universitas jember fakultas ekonomi'.

Nari, N. and Musfika, A.P. (2016) 'Analisis Kesulitan Belajar Ditinjau dari Kemampuan Koneksi Matematika Peserta Didik', IAIN Batusangkar, (1), pp. 311--320. Available at: https://ojs.iainbatusangkar.ac.id/ojs/index.php/proceedings/article/viewFile/653/643.

Nurdin, E., Nufus, H. and Hasanuddin (2018) 'Pengaruh Pendekatan Visual Thinking Terhadap', KALIMATIKA Jurnal Pendidikan Matematika, 3(1), pp. 17--26.

Pambudi, D.S., Budayasa, I.K. and Lukito, A. (2020) 'The Role of Mathematical Connections in Mathematical Problem Solving', Jurnal Pendidikan Matematika, 14(2), pp. 129--144. Available at: https://doi.org/10.22342/jpm.14.2.10985.129-144.

Prihartini, N., Puspita Sari and Ibnu Hadi (2020) 'Design Research: Mengembangkan Pembelajaran Konsep Peluang Dengan Pendekatan Pendidikan Matematika Realistik Indonesia Pada Siswa Kelas IX di SMPN 220 Jakarta', Jurnal Riset Pembelajaran Matematika Sekolah, 4(1), pp. 1--8. Available at: https://doi.org/10.21009/jrpms.041.01.

Rahmawati, U.N. et al. (2017) 'Kesulitan Koneksi Matematis Siswa dalam Menyelesaikan Soal Cerita Materi Peluang di Sekolah Menengah Atas', Jurnal Pendidikan dan Pembelajaran Khatulistiwa, 6(8), pp. 1--14.

Sholekah, L.M., Anggreini, D. and Waluyo, A. (2017) 'Analisis Kesulitan Siswa Dalam Menyelesaikan Soal Matematika Ditinjau Dari Koneksi Matematis Materi Limit Fungsi', WACANA AKADEMIKA: Majalah Ilmiah Kependidikan, 1(2), pp. 151--164. Available at: https://doi.org/10.30738/wa.v1i2.1413.

Siagian, M.D. (2016) 'Kemampuan koneksi matematik dalam pembelajaran matematika', MES: Journal of Matematics Education and Science2, 2(1), pp. 58--67.

Susanty, A. (2018) 'Analisis Kemampuan Koneksi Matematis Berdasarkan Nctm Siswa Sma Kelas X Ipa Pada Materi Eksponen Dan Logaritma', Jurnal Pendidikan Tambusai, 2(4), pp. 870--876.

Wahidah, S.W. and Qudsyi, H. (2011) 'Pengaruh interferensi dan rehearsal terhadap the effect of interference and rehearsal toward english retention among students of the islamic', Jurnal Intervensi Psikologi, 3(2), pp. 257--273.

Zainudin, M., Utami, A.D. and Noviana, S. (2021) 'Analisis kesulitan siswa dalam menyelesaikan soal peluang ditinjau dari koneksi matematis', Suska Journal of Mathematics Education, 7(1), pp. 41--48.