Berapa Kemungkinan Ahok Menang Pilkada dalam 1 Putaran?

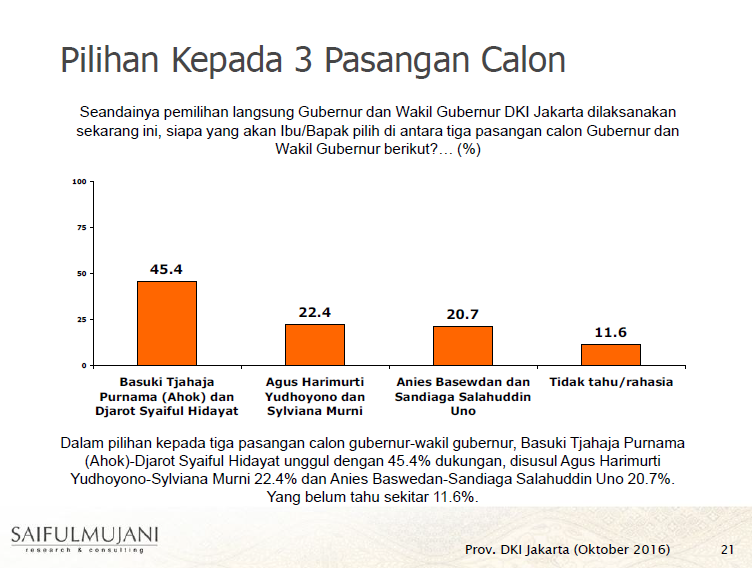
Kemarin saya menerima WhatsApp dari kakak saya mengenai hal yang sangat menarik bagi saya. Kakak saya memaparkan data yang baru saja dirilis SMRC (Saiful Mujani Research & Consulting) mengenai pilihan penduduk Jakarta untuk calon Gubernur. Menurut presentasi yang dirilis dari 648 responden, 294 orang (45.4%) memilih Ahok-Djarot, 145 orang (22.4%) memilih Agus-Sylviana, 134 orang (20.7%) memilih Anies-Sandiaga, dan 75 orang (11.6%) rahasia atau belum memiliki pilihan. Pertanyaan yang dilontarkan kakak saya sangat menarik, "berapa persen kemungkinan Ahok menang dalam 1 putaran?" Diketahui bahwa untuk menang dalam 1 putaran, diperlukan suara sebanyak 50% dari pemilih.

Untuk menjawab pertanyaan tersebut, saya membuat asumsi bahwa sampling dilakukan secara acak (random sampling) di seluruh Jakarta. Walaupun metode pengumpulan datanya menggunakan multistage random sampling, tapi untuk membuat model yang lebih akurat memerlukan data dan waktu yang cukup banyak. Jadi menggunakan asumsi random sampling dapat menyederhanakan metode dan jawaban yang diperoleh pun tidak jauh dengan apabila menggunakan model multistage random sampling.

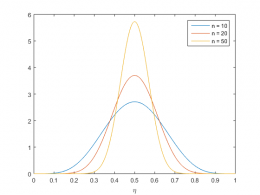
Dengan random sampling, distribusi beta dapat digunakan untuk menggambarkan proporsi pemilih dari data hasil penarikan sampel dari populasi yang sangat besar. Misalnya saya memiliki jutaan kelereng kecil disimpan di satu wadah (yang sangat besar), ada yang berwarna merah dan ada yang biru. Apabila saat menarik 10 kelereng, terdapat 5 kelereng yang berwarna merah dan 5 kelereng yang berwarna biru. Apakah berarti perbandingan jumlah total kelereng berwarna merah dan biru adalah 50:50? Jawabannya belum tentu. Untuk mengetahui porsi kelereng berwarna merah, dapat menggunakan distribusi beta tersebut. Distribusi kemungkinan porsi kelereng berwarna merah dapat dilihat di gambar di bawah ini apabila diambil (n) 10, 20, dan 50 kelereng dan didapatkan setengah dari kelereng yang diambil adalah kelereng berwarna merah. Aksis horizontal menunjukkan porsi kelereng berwarna merah di wadah tersebut dan aksis vertikal menunjukkan seberapa mungkin porsi tersebut, semakin tinggi semakin mungkin.

Sumber Data: http://sp.mfkasim.com/

Seperti yang dilihat di atas, apabila cuma diambil 10 kelereng dan didapatkan 5 berwarna merah, masih ada kemungkinan bahwa rasio kelereng berwarna merah dari seluruh kelereng adalah ~25%-75%. Apabila diambil 50 kelereng dan terdapat 25 berwarna merah di antaranya, rentangnya menjadi semakin kecil (~35% - 65%).

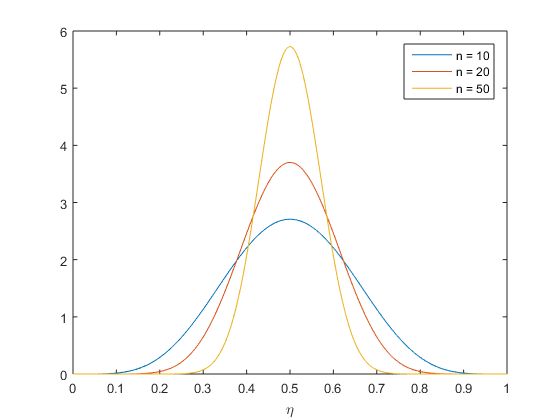
Kemungkinan kesalahan (margin of error) distribusi beta dapat didekatkan dengan formula ~100%/akar(jumlah sampel). Hal ini sesuai dengan yang dikatakan di presentasi SMRC (di halaman 3) bahwa dengan 648 sampel, margin of error-nya adalah 3.9% (100%/akar(648) ~ 3.93%).

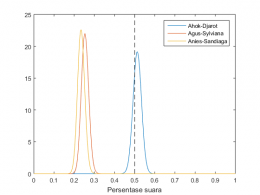
Sekarang mari kembali ke kasus Pilkada DKI. Dari 648 responden, hanya 573 yang memberikan jawaban pasti. Dan dari 573 suara tersebut, 294 (51.3%) memilih Ahok-Djarot, 145 (25.3%) memilih Agus-Sylviana, dan 134 (23.4%) memilih Anies-Sandiaga. Distribusi beta berdasarkan data tersebut adalah sebagai berikut.

Sumber Data: http://sp.mfkasim.com/

Dari grafik di atas dapat dilihat bahwa persentase suara Ahok-Djarot cukup jauh dibandingkan kedua pasangan calon lainnya. Apabila Pilkada dilakukan sekarang, hampir dapat dipastikan Ahok akan menang. Persentase suara Agus-Sylviana dan Anies-Sandiaga masih sangat dekat dan cukup sulit memprediksi saat ini siapa yang mendapatkan urutan kedua.

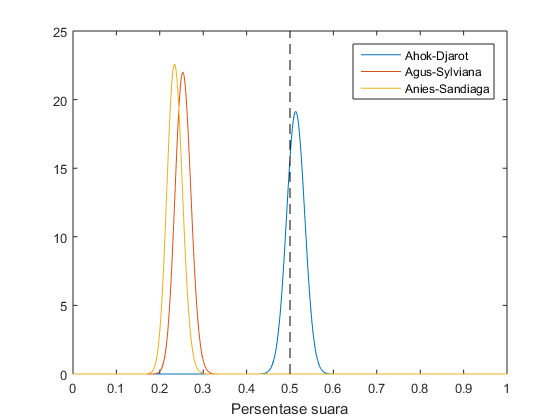
Untuk menghitung berapa kemungkinan Ahok menang Pilkada dalam 1 putaran (apabila Pilkada dilakukan saat ini), kita dapat menghitung area grafik berwarna biru di sebelah kanan garis putus-putus hitam. Ini menunjukkan berapa kemungkinan Ahok akan mendulang lebih dari 50% suara dari seluruh populasi. Dengan menghitung area tersebut, kita mendapatkan nilai 0.735. Artinya kemungkinan Ahok menang Pilkada dalam 1 putaran (apabila Pilkada dilakukan saat ini) adalah 73.5%.

Perlu diketahui bahwa ini adalah hasil statistik untuk data saat ini yang masih sangat mungkin berubah saat Pilkada 2017 nanti berlangsung. Dan satu lagi, mendapatkan kemungkinan yang cukup besar untuk menang dalam 1 putaran bukan berarti sudah pasti akan menang dalam 1 putaran. Masih ada kemungkinan untuk Ahok tidak menang dalam 1 putaran, bahkan masih ada kemungkinan calon yang lain yang akan menang. Saya tidak memihak siapa pun dalam menuliskan artikel ini. Ini hanya untuk memuaskan rasa ingin tahu saya sekaligus mengasah kemampuan saya dalam menghitung statistik. Versi detail (termasuk penurunan rumus) dalam bahasa Inggris bisa dibaca di sini.