Modul Ajar Informatika Berpikir Komputasional Kelas VIII Kurikulum Merdeka

INFORMASI UMUM

1. Identifikasi Sekolah

Penyusun                            : Nabil Makarim

Sekolah                                : SMP Al Islam 1 Surakarta

Mata Pelajaran                 : Informatika

Kelas/ Semester               : VIII / Gasal

Fase                                       : D

Materi Pokok                     : Berpikir Komputasional

Alokasi Waktu                   : 1 Pertemuan x 2 jam pelajaran @ 35 Menit

Jumlah Peserta didik      : Maksimal 36 Siswa

Target Peserta didik       : Reguler

Model Pembelajaran      : Problem Base Learning (PBL)

2. Kompetensi Awal

Kompetensi awal yang harus dimiliki oleh peserta didik sebelum mempelajari topik ini adalah kemampuan dan pemahaman mengenai Berpikir komputasional, penyelesaian masalah, algoritma, representasi data, struktur data, sistem bilangan.

3. Profil Pancasila

Beriman,  bertaqwa kepada  YME dan berakhlak mulia: Kemampuan untuk memahami ajaran agama dan kepercayaannya serta menerapkan pemahaman tersebut dalam kehidupannya sehari-hari

Gotong royong: Kemampuan untuk bekerja sama dengan orang lain disertai perasaan senang ketika berada bersama dengan orang lain dan menunjukkan sikap positif terhadap orang lain

Bernalar Kritis: Melalui informasi yang didapat dapat menggunakannya untuk menganalisis permasalahan maupun informasi

Mandiri: Dengan kemampuan sendiri mencari informasi yang dapat dipertanggung jawabkan kebenarannya

4. Sarana dan Prasarana (Sumber Belajar)

Sarana          : Lab. Komputer/Ruang Kelas, PC/Laptop, Alat tulis, Buku tulis, LCD, Proyektor.

Prasarana   : Internet, Buku paket Informatika kelas VIII, Modul Ajar.

5. Target Peserta Didik

Siswa Reguler

6. Model Pembelajaran

Model pembelajaran yang digunakan dalam pembelajaran materi Berpikir Komputasional ialah Problem Based Learning (PBL).

KOMPONEN INTI

A. ELEMEN

 

Berpikir Komputasional (BK)

B. CAPAIAN PEMBELAJARAN

C. TUJUAN PEMBELAJARAN

• Peserta didik mampu menjelaskan bahwa sebuah kasus persoalan logika dapat dimodelkan dengan model tertentu, yang salah satunya dalam soal ini model yang digunakan adalah himpunan
• Peserta didik mampu menjelaskan konsep representasi data.
• Peserta didik mampu menjelaskan konsep data yang direpresentasikan dalam bilangan biner, oktal, dan desimal, dan melakukan konversi bilangan dari satu representasi ke representasi lainnya.

D. ASESMEN

Formatif

a. Pengetahuan  : Tes Tulis

b. Sikap            : Observasi

E. PEMAHAMAN BERMAKNA

Peserta didik mempelajari  konsep berpikir komputasional, yang melibatkan pemecahan masalah dengan pendekatan logis dan sistematis. Peserta didik akan belajar tentang bagaimana cara pemikiran komputasional dapat diterapkan dalam pemecahan masalah sehari-hari.

Peserta didik mempelajari konsep himpunan tentang operasi dasar himpunan, seperti penggabungan, irisan, dan perbedaan.

Peserta didik memahami berbagai sistem bilangan, seperti desimal, biner, oktal, dan heksadesimal.

F. PERTANYAAN PEMATIK

Pertanyaan pemantik untuk peserta didik sebagai berikut.

• Apa itu himpunan dan sistem bilangan, dan bagaimana konsep ini dapat diterapkan dalam berpikir komputasional ?
• Bagaimana menggunakan operasi himpunan, seperti gabungan, irisan, dan selisih, dalam pemecahan masalah komputasi ?
• Mengapa pemahaman tentang sistem bilangan, seperti desimal, biner, dan heksadesimal, penting dalam komputasi?
• Bagaimana cara melakukan konversi bilangan dari satu sistem bilangan ke sistem bilangan lainnya ?

G. KEGIATAN PEMBELAJARAN

Kegiatan Pendahuluan (10 menit)

• Guru membuka kegiatan pembelajaran dengan mengucapkan salam
• Siswa melakukan do’a sebelum belajar (Guru meminta seorang Siswa untuk memimpin do’a).
• Guru mengecek kehadiran Siswa dan meminta siswa untuk mempersiapkan perlengkapan dan peralatan yang diperlukan.
• Siswa menerima informasi tentang pembelajaran yang akan dilaksanakan dengan materi himpunan dan sistem bilangan.
• Guru memberikan permasalahan sehari-hari yang dimodelkan dengan konsep himpunan dan sistem bilangan.

 

Kegiatan Inti (50 menit)

a. Orientasi Masalah

• Guru bertanya tentang konsep himpunan dan sistem bilangan serta bagaimana mengoperasikannya
• Siswa diminta untuk menyampaikan pendapat  dalam konsep himpunan dan sistem bilangan
• Siswa diminta untuk menarik kesimpulan tentang himpunan dan sistem bilangan
• Guru mendorong siswa untuk mempelajari dan mengumpulkan informasi lain dari berbagai sumber untuk memahami himpunan dan sistem bilangan

b. Mengorganisasi Siswa

• Guru membagi kelompok yang beranggotakan 3 - 4 siswa
• Siswa diminta menyimak secara saksama media pembelajaran yang ditampilkan guru untuk penerapan himpunan dan sistem bilangan
• Guru memberikan lembar kerja kepada setiap kelompok untuk menyelesaikan persoalan dalam himpunan dan sistem bilangan
• Guru berkeliling untuk melihat kegiatan yang dilakukan siswa
• Guru melihat sampel pekerjaan siswa setiap kelompok dan berdiskusi tentang apa yang sudah dilakukan.
• Guru memberikan bantuan terbatas, apabila ada siswa atau kelompok yang mengalami kesulitan

d. Mengembangkan dan Menyajikan Hasil Karya

• Guru meminta dengan sukarela kepada perwakilan kelompok untuk mempresentasikan lembar kerja hasil dari diskusi antar anggota kelompok
• Kelompok lain diminta untuk menanggapi dan memberikan argumen tentang apa yang dipresentasikan.
• Guru meminta perwakilan kelompok lain untuk mempresentasikan hasil diskusinya
• Kelompok lain diminta kembali untuk menanggapi dan memberikan argumen tentang apa yang dipresentasikan

e. Menganalisis dan Mengevaluasi Proses Pemecahan Masalah

• Guru meminta semua siswa untuk saling melakukan apresiasi terhadap kelompok yang telah sukarela mempresentasikan hasil diskusi dan siswa yang sudah terlibat aktif dalam pembelajaran
• Guru memberikan tambahan atau penguat apabila ada pendapat siswa yang kurang sesuai
• Guru memberikan contoh soal himpunan dan sistem bilangan untuk mengecek pemahaman siswa dan memberikan umpan balik pembelajaran

Kegiatan Penutup (10 menit)

• Guru bersama siswa melakukan refleksi mengenai pembelajaran yang telah dilakukan
• Guru mengkonfirmasi materi yang akan dibahas pada pertemuan berikutnya
• Guru bersama siswa mengakhiri pembelajaran dengan membaca do’a
• Guru menutup pembelajaran dengan mengucapkan salam

H. PENGAYAAN DAN REMIDIAL

Pengayaan

Diberikan terhadap siswa yang capaian pembelajarannya telah tuntas untuk menambah wawasan kepada siswa mengenai materi pembelajaran.

• Guru memberikan siswa pemahaman lebih mendalam tentang sistem bilangan lanjutan seperti oktal dan basis lainnya selain biner, desimal, dan heksadesimal
• Guru mengajarkan siswa tentang sistem bilangan oktal, biner dan bagaimana mengonversi angka desimal ke oktal atau biner dan sebaliknya.

Remidial

Diberikan terhadap siswa yang belum memahami materi dengan baik serta kepada siswa yang capaian pembelajarannya belum tuntas

• Guru mengatur siswa untuk berkelompok dan melakukan  sesi diskusi supaya dapat bertanya kepada guru tentang hal-hal yang belum dipahami.
• Guru mengajarkan dasar-dasar himpunan kepada siswa dengan contoh yang lebih sederhana dan mudah dimengerti.

I. REFLEKSI PESERTA DIDIK DAN GURU

Refleksi Peserta Didik

• Bagaimana pemahaman kamu tentang sistem bilangan (seperti desimal, biner, dan heksadesimal) telah berkembang selama pembelajaran ini?
• Bagaimana sistem bilangan digunakan dalam komputasi sehari-hari?
• Apa yang telah kamu pelajari tentang konsep himpunan?
• Apakah ada bagian dari materi ini yang masih membingungkan atau memerlukan penjelasan lebih lanjut?
• Apakah kamu memiliki pertanyaan yang belum terjawab?
• Bagaimana kamu merasa tentang kemampuan kamu untuk menerapkan pemahaman tentang himpunan dan sistem bilangan dalam pemecahan masalah atau proyek yang melibatkan komputasi?

Refleksi Guru

• Bagaimana respons siswa terhadap materi tentang sistem bilangan dan himpunan?
• Apakah metode dan strategi pengajaran yang digunakan efektif dalam membantu siswa memahami konsep sistem bilangan dan himpunan?
• Apakah materi ini disajikan dalam konteks yang relevan bagi siswa?
• Apakah evaluasi dan penilaian yang digunakan mencerminkan pemahaman siswa tentang materi ini?
• Apakah ada siswa yang memerlukan bantuan tambahan atau remidial dalam pemahaman materi ini?
• Apakah ada hambatan atau tantangan khusus yang dihadapi dalam pengajaran materi ini?

A. Glosarium

algoritma; algorithm :  langkah-langkah dari proses untuk mencapai tujuan tertentu antarmuka aplikasi; application interface Ruang tempat interaksi antara pengguna dengan perangkat lunak aplikasi

bilangan biner : bilangan yang ditulis dalam sistem bilangan berbasis 2, contoh: bilangan 4 ditulis menjadi 100

bilangan desimal : bilangan yang ditulis dalam sistem bilangan berbasis 10. Tiap digit bilangan desimal terdiri atas bilangan 0 sampai 9

biner; binary biner : metode untuk mengkodekan data dengan dua simbol, 1 dan 0.

desimal; decimal : sistem bilangan yang menggunakan basis sepuluh

himpunan; set kumpulan data atau objek yang dapat diketahu

oktal; octal : sistem bilangan dengan menggunakan basis 8

sistem bilangan : kumpulan simbol khusus yang digunakan dalam membangun sebuah bilangan. 

sistem heksadesimal : sistem bilangan menggunakan basis 16, enam belas digit heksadesimal biasanya diwakili oleh angka 0-9, dan huruf A-F

B. Daftar Pustaka

Informasi, F. T., & Nikijuluw, J. L. (2015). Artikel Ilmiah Program Studi Pendidikan Teknik Informatika dan Komputer Fakultas Teknologi Informasi Universitas Kristen SatyaWacana Salatiga Juni 2015.

Minarti, I. B., Nurwahyunani, A., Fajriyah, S. A., Dzakiyatus, S., Valenta, V., Ardian, K., Lestari, S. A., & Handrian, D. (2023). “Integrasi Model Problem Based Learning ( PBL ) dalam meningkatkan Hasil Belajar dan Motivasi siswa di indonesia.” 1, 44–54.

Wijanto, M. C. (2021). Informatika SMP Kelas VII.

      

Surakarta, 15 Oktober 2023                                   

Mengetahui,

Kepala SMP Al-Islam 1 Surakarta

Supardi, S.Pd

Guru Informatika

Nabil Makarim

LAMPIRAN 1 

BAHAN AJAR

Himpunan dan Sistem Bilangan

1. Himpunan

A. Pengertian Himpunan 

Himpunan adalah kumpulan benda atau objek-objek atau lambang-lambang yang mempunyai arti yang dapat didefinisikan dengan jelas mana yang merupakan anggota himpunan dan mana bukan anggota himpunan. Objek-objek tersebut disebut elemen. Contoh himpunan adalah himpunan buah-buahan, himpunan bilangan genap, dan himpunan siswa kelas 8 SMP.

B. Notasi Himpunan

Notasi himpunan adalah cara untuk menuliskan himpunan. Notasi himpunan terdiri dari kurung kurawal { } dan elemen-elemennya dipisahkan dengan tanda koma. Contoh notasi himpunan adalah {apel, jeruk, mangga} dan {2, 4, 6, 8, 10}.

C. Operasi Himpunan

Operasi himpunan adalah cara untuk memanipulasi himpunan. Ada beberapa operasi himpunan, yaitu:

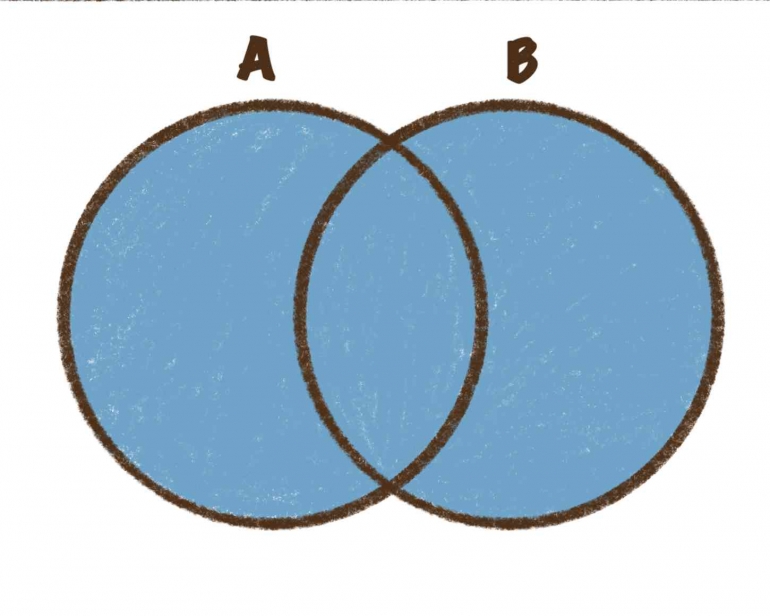
• Gabungan (union) 

Gabungan dari himpunan A dan B adalah himpunan yang berisi semua elemen dari anggota himpunan A dan himpunan B. Notasi gabungan adalah A ∪ B =  {x ∣ x ∈ A atau x ∈ B}.

Gambar 1.1 Diagram Venn Gabungan

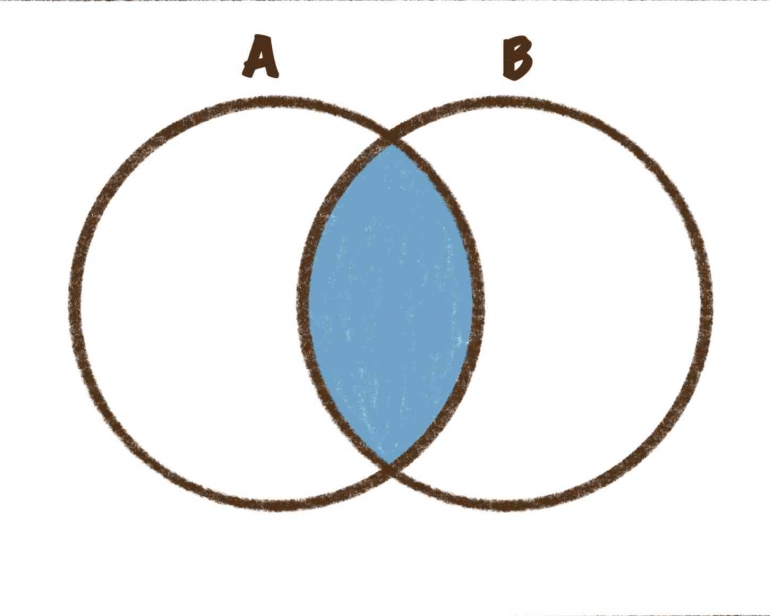
• Irisan (intersection)

Irisan dari himpunan A dan B adalah himpunan yang berisi elemen-elemen yang dimiliki oleh himpunan A dan himpunan B. Notasi irisan adalah A ∩ B = {x ∣ x ∈ A dan x ∈ B}.

Gambar 1.2 Diagram Venn Irisan

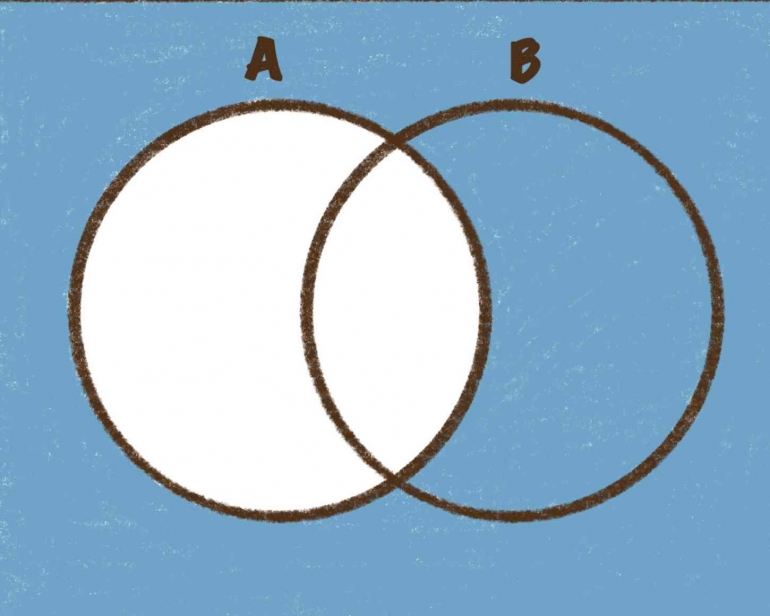
• Selisih (Difference) 

Selisih dari himpunan A dan B adalah himpunan yang berisi elemen-elemen yang dimiliki oleh himpunan A tetapi tidak dimiliki oleh himpunan B. Selisih himpunan A dan B adalah komplemen himpunan B terhadap himpunan A. Notasi selisih adalah A – B = {x | x Є A dan x Є B}.

Gambar 1.3 Diagram Venn Selisih

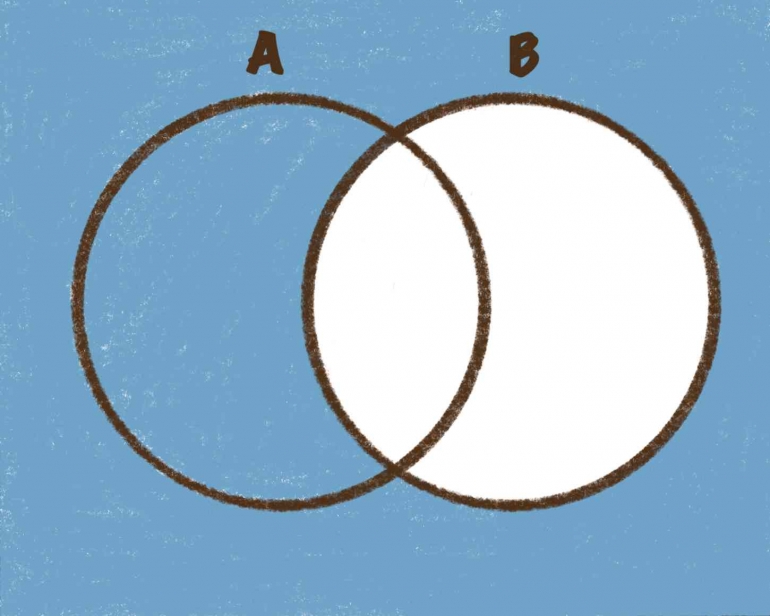
• Komplemen (complement)

Operasi himpunan komplemen antara dua himpunan A dan B menghasilkan himpunan yang terdiri dari elemen-elemen yang ada di himpunan A, tetapi tidak ada di himpunan B. Notasi komplemen adalah A’ ={x ∣ x ∈ A dan x ∈ / B}.

Gambar 1.4 Diagram Venn Komplemen

D. Ilustrasi Himpunan

Banyak hal dalam kehidupan sehari-hari dapat direpresentasikan dalam bentuk himpunan. Kita dapat mengambil kesimpulan dari pengolahan himpunan. Mari, kita lihat contoh sederhana berikut ini.

Adik suka buah jeruk, mangga, dan jambu. Kakak suka rambutan, mangga, duku, dan buah naga. Seseorang bertanya kepada kalian dua buah pertanyaan. Pertanyaan pertama, “Buah apa sajakah yang disukai adik atau kakak?” Pertanyaan kedua, “Buah apa sajakah yang disukai adik dan kakak?” Tentunya, jawaban kalian berbeda. Untuk menjawab dua buah pertanyaan tersebut, kalian dapat menuliskan himpunan buah kesukaan adik dan kakak. Buah kesukaan adik = {jeruk, mangga, jambu}. Buah kesukaan kakak = {rambutan, mangga, duku, buah naga}. Untuk menjawab pertanyaan pertama, kalian perlu mencari hasil gabungan dari kedua himpunan tersebut yang menghasilkan himpunan baru, yaitu {jeruk, mangga, jambu, rambutan, duku, buah naga}. Untuk menjawab pertanyaan kedua, kalian perlu mencari irisan dari kedua himpunan tersebut, yaitu {mangga}.

2. Sistem Bilangan

A. Pengertian Sistem Bilangan

Sistem bilangan adalah aturan dan notasi yang digunakan untuk menggambarkan dan merepresentasikan angka. Terdapat beberapa sistem bilangan yang digunakan dalam informatika yaitu:

• Bilangan Desimal 

Sistem bilangan desimal adalah sistem bilangan yang menggunakan basis 10 (deca). Menggunakan 10 macam simbol bilangan yaitu 0, 1, 2, 3, 4, 5, 6, 7, 8, dan 9.

• Bilangan Biner 

Sistem bilangan biner adalah sistem bilangan yang menggunakan basis 2. Menggunakan 2 simbol bilangan yaitu 0 dan 1.

• Bilangan Oktal

Sistem bilangan oktal adalah sistem bilangan yang menggunakan basis 8 (octal). Menggunakan 8 macam symbol bilangan yaitu 0, 1, 2, 3, 4, 5, 6, dan 7.

• Bilangan Heksadesimal 

Sistem bilangan heksadesimal adalah sistem bilangan yang menggunakan basis 16 (hexa). Menggunakan 16 macam simbol bilangan yaitu 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, dan F.

B. Konversi Sistem Bilangan

Konversi sistem bilangan adalah cara untuk mengubah bilangan dari satu sistem bilangan ke sistem bilangan lain. Ada beberapa cara untuk melakukan konversi sistem bilangan, yaitu:

• Konversi Desimal ke Biner 

Bilangan desimal dapat dikonversi ke bilangan biner dengan cara membagi bilangan desimal tersebut dengan 2 dan menyimpan sisa bagi. Contoh: 10 (desimal) = 1010 (biner).

• Konversi Biner ke Desimal  

Bilangan biner dapat dikonversi ke bilangan desimal dengan cara menjumlahkan setiap digit biner yang bernilai 1 dengan pangkat 2 yang sesuai. Contoh: 1010 (biner) = 10 (desimal).

• Konversi Desimal ke Oktal 

Bilangan desimal dapat dikonversi ke bilangan oktal dengan cara membagi bilangan desimal tersebut dengan 8 dan menyimpan sisa bagi. Contoh: 10 (desimal) = 12 (oktal).

• Konversi Oktal ke Desimal 

Bilangan oktal dapat dikonversi ke bilangan desimal dengan cara menjumlahkan setiap digit oktal dengan pangkat 8 yang sesuai. Contoh: 12 (oktal) = 10 (desimal).

• Konversi Desimal ke Heksadesimal 

Bilangan desimal dapat dikonversi ke bilangan heksadesimal dengan cara membagi bilangan desimal tersebut dengan 16 dan menyimpan sisa bagi. Jika sisa bagi lebih besar dari 9, maka diganti dengan huruf A-F. Contoh: 10 (desimal) = A (heksadesimal).

• Konversi Heksadesimal ke Desimal 

Bilangan heksadesimal dapat dikonversi ke bilangan desimal dengan cara menjumlahkan setiap digit heksadesimal dengan pangkat 16 yang sesuai. Contoh: A (heksadesimal) = 10 (desimal).

C. Ilustrasi Sistem Bilangan

Pernahkah kalian memperhatikan pergantian bilangan-bilangan yang ada pada timbangan digital? Bilangan yang ditunjukkan pada layar timbangan digital pada Gambar 2.1 adalah bilangan desimal (berbasis 10). Mari, kita menyimulasikan dan mempelajari konsep dari bilangan desimal dengan menggunakan bilangan 2789.

Ditampilkan sebuah bilangan yang terdiri atas empat buah angka 0. Dalam sistem bilangan desimal yang berbasis 10, setiap digit pembentuk bilangan tersebut dapat bernilai 0-9. Dalam kasus timbangan digital, jika kalian perhatikan dengan saksama, digit yang pertama akan berubah ketika sebuah benda diletakkan di atasnya adalah digit yang berada pada posisi paling kanan. Digit tersebut akan berubah dari 0, 1, 2, 3, dan seterusnya hingga ada kemungkinan mencapai angka 9 (0009). Jika ternyata bilangan 9 tersebut belum mencukupi, bilangan yang kedua dari kanan akan berubah dari 0 menjadi 1, sedangkan digit paling kanan kembali menjadi 0 (0010). Kemudian, digit paling kanan akan berganti lagi dalam rentang 0 sampai dengan 9. Hal tersebut terus berlangsung hingga timbangan mencapai angka yang menunjukkan berat dari benda atau timbangan menunjukkan angka maksimalnya dengan 4 digit, yaitu 9999.

LAMPIRAN 2

LEMBAR KERJA PESERTA DIDIK