Persegi adalah bahasa Indonesia dari square, sebelumnya disebut bujur sangkar. Sebenarnya kata "ajaib" tidak tepat jika yang kita bicarakan adalah matematika, namun istilah ini saya gunakan karena juga terdapat dalam bab pertama buku pertama dari 4 Buku Catatan Srinivasa Ramanujan yang dikompilasi oleh Bruce C. Berndt. Siapa Ramanujan akan saya tuangkan dalam sebuah artikel lain. Bilangan yang bisa diisikan ke dalam sebuah persegi ajaib n x n bisa dihitung dengan rumus Ramanujan.
Namun, untuk tujuan bermain game, saya hanya akan menggunakan persegi ajaib 3 x 3 (9 kotak) yang bisa diisi dengan 9 bilangan yang berurutan, yang artinya memiliki kemungkinan yang tidak terbatas. Game ini sangat sederhana dan hanya butuh kertas dan pena, sangat cocok untuk berinteraksi dengan anak tanpa menggunakan HP sekaligus mengasah kreativitas anak, dalam hal ini adalah membuat sendiri kemungkinan lain, dan pada gilirannya si anak bisa mengajak temannya bermain, atau meneruskan bermain dengan mengganti siapa yang membuat kemungkinan 9 bilangan itu. Ketentuan: 9 bilangan tersebut harus memiliki selisih yang sama: n, n+a, ............ n+8a.
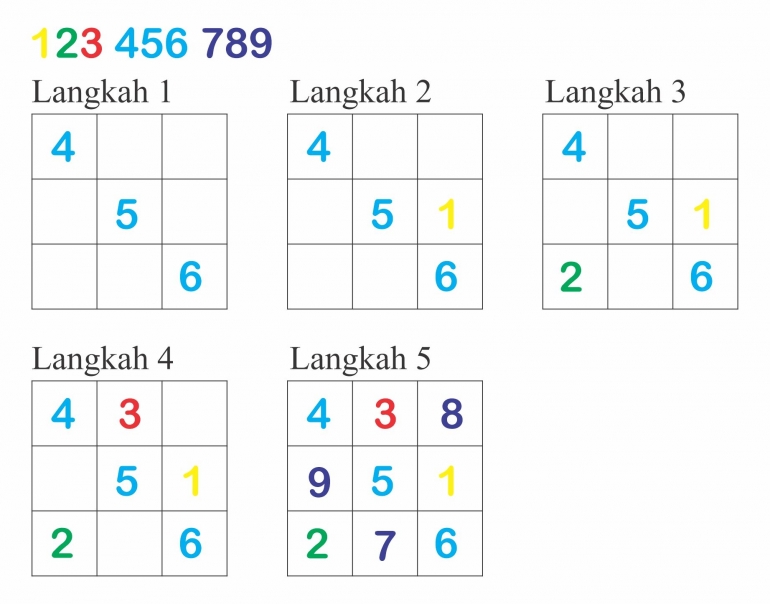
Bagi saya, game ini semula terlihat rumit, tapi setelah mengamati cara mengisi kotak itu, saya mendapatkan hanya 1 cara dengan 5 langkah penyelesaian, yang berarti gamenya langsung selesai. Itulah sebabnya saya katakan tentang kreativitas anak yang berkaitan dengan pembuatan kemungkinan/pilihan.
Pertama-tama, gambarkan sebuah persegi 3 x 3, lalu tuliskan 9 bilangan yang hendak diisikan ke dalamnya, misalnya: 1, 2, 3, 4, 5, 6, 7, 8, dan 9.
5 langkah yang saya maksudkan adalah:
1. Cari jumlah 3 bilangan yang di median (4 + 5 + 6 = 15) lalu isikan ketiga bilangan ini secara diagonal ke dalam persegi. Ini berarti bahwa jumlah bilangan secara, horizontal, vertikal, maupun diagonal adalah 15.
2. Di atas bilangan terakhir median (6), isikan bilangan terkecil (1).
3. Lanjutkan dengan bilangan berikutnya (2) dengan meletakkannya pada posisi jalannya kuda catur (huruf L).
4. Bilangan 3 diisi dengan cara yang sama dengan no. 3 di atas.
5. Sisa bilangan disusun berdasarkan jumlahnya secara horizontal dan vertikal = 15, atau bilangan 7 diisikan ke kotak di sebelah kiri bilangan terakhir median (6), lalu lanjutkan dengan cara no. 3 dan no. 4 untuk bilangan 8 dan 9.
Selesai.
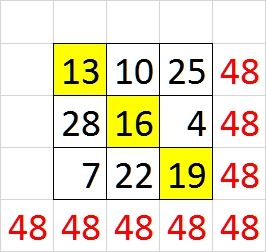
1. Urutan bilangan yang dimulai dengan 4 dan penambahan 3: 4, 7, 10, 13, 16, 19, 22, 25, dan 28.
Selamat bermain.
Jonggol, 29 April 2021
Johan Japardi
