Ars Magna dikenal sebagai karya monumental yang ditulis oleh Girolamo Cardano, seorang ahli matematika jenius pada abad ke-16. Karya ini telah menjadi tonggak penting dalam sejarah matematika dan memberikan kontribusi luar biasa untuk memecahkan persamaan kubik matematika. Dalam Ars Magna, Cardano melibatkan manipulasi aljabar dan penggunaan bilangan negatif dalam pemecahan persamaan matematika. Meskipun bilangan negatif telah dikenal di Eropa melalui teks-teks Arab, namun kebanyakan ahli aljabar Barat tidak menerimanya dan lebih suka menulis persamaannya sehingga hanya suku positif yang muncul (Burton, 2011). Dengan adanya konsep ini pada saat itu dinilai melanggar oleh pandangan konvensional, tetapi membuka jalan bagi perkembangan aljabar modern dan memperluas pemahaman kita tentang bilangan. Karena hal itu, Cardano adalah orang pertama yang menyadari solusi akar negatif dan menyadari bahwa kubik dapat memiliki tiga akar.
Cardano telah memperkenalkan metode baru untuk menyelesaikan persamaan kubik yang sebelumnya dianggap sulit atau bahkan tidak mungkin diselesaikan, metode ini dapat dikenal sebagai "Metode Cardano". Penemuan Cardano ini mempengaruhi banyak matematikawan dan ilmuwan setelahnya, termasuk Rene Descartes dan Isaac Newton. Cardano menjelaskan bahwa dia mengenali keberadaan sebuah bilangan, yang sekarang dikenal sebagai bilangan imajiner, tetapi tidak mengetahui sifat-sifatnya. Dengan inovasi yang diperkenalkan oleh Cardano di Ars Magna salah satu triknya yaitu dengan mengubah persamaan kubik menjadi persamaan kuadrat tak terhingga atau persamaan yang tidak memiliki suku derajat dua. (Susilawati, 2017) untuk menyelesaikan permasalahan persamaan pangkat tiga yang diberikan oleh Cardano dalam Ars Magna, yaitu sebagai berikut:
Jika a dan b dinyatakan dalam bentuk
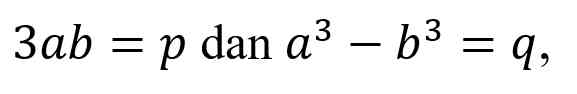
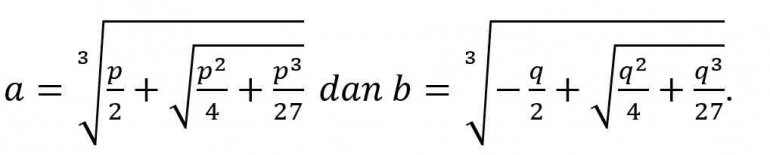
Dengan demikian,
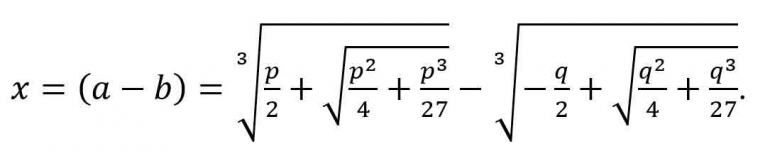
. Akan tetapi ada kesulitan terkait dengan formula terakhir ini, yang diamati oleh Cardano tetapi tidak bisa diselesaikan. Ketika
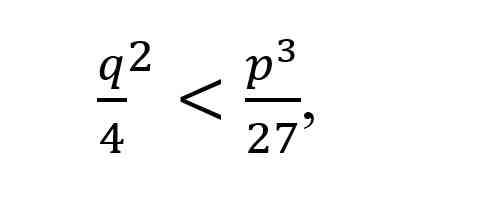
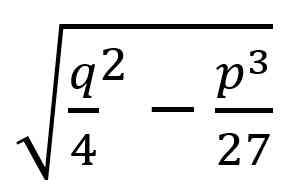
Selain itu, Ars Magna mencakup konsep matematika penting lainnya seperti permutasi, kombinatorik, dan probabilitas. Cardano menggabungkan pendekatan geometris dan aljabar dalam karya ini, yang mengarah pada pemikiran inovatif dan sistematis dalam pemecahan masalah. Cardano menghubungkan setiap bentuk ke representasi diagram persamaan kubik (Morgan G. Ames dan Massimo Mazzoti, 2022). Pendekatan ini memunculkan pemikiran analitis terstruktur, yang menjadi dasar kemajuan selanjutnya dalam matematika. Konsep dan prinsip yang diperkenalkan dalam Ars Magna tidak hanya berdampak dalam matematika, tetapi juga di bidang lain seperti fisika, teknik, dan komputer. Dalam fisika, misalnya, penggunaan bilangan kompleks yang diperkenalkan oleh Cardano sangat penting dalam memodelkan fenomena gelombang, osilasi, dan mekanika kuantum. Sedangkan dalam bidang komputer dan kecerdasan buatan, pendekatan sistematis dan logika yang diperkenalkan dalam Ars Magna masih digunakan dalam pengembangan algoritma dan pemecahan masalah kompleks. Prinsip-prinsip dalam Ars Magna telah diadopsi dalam desain dan implementasi algoritma, pemodelan matematis, dan pengembangan teknik optimisasi yang digunakan dalam komputasi modern. Metode Cardano dalam memecahkan masalah matematika kompleks, telah dijadikan landasan dalam pemahaman dan penelitian dalam berbagai cabang ilmu pengetahuan alam.
Ars Magna tetap relevan dalam konteks perkembangan matematika dan sains yang berkembang saat ini. Kontribusi Cardano untuk memecahkan persamaan kubik dan pendekatan sistematisnya meletakkan dasar bagi perkembangan matematika modern untuk terus menginspirasi para peneliti dan pemikir dalam memecahkan masalah yang kompleks. Karya ini menunjukkan bagaimana keberanian untuk berpikir di luar batas-batas konvensional dan mengeksplorasi konsep-konsep baru yang dapat menghasilkan terobosan dan inovasi yang signifikan.
DAFTAR PUSTAKA













