Banyak sekali orang mengatakan bahwa matematika itu ilmu yang sulit dipelajari. Salah satunya adalah perkalian. Perkalian merupakan salah satu bentuk operasi matematika yang sangat penting dalam kehidupan sehari-hari, tetapi juga sulit dipahami oleh siswa khususnya sekolah dasar. Kesulitan akan terus berlanjut ketika para siswa mulai dihadapkan oleh perkalian pada tigkat puluhan, ratusan, bahkan ribuan. Tapi taukah sobat maths? Banyak juga metode-matode yang dapat mempermudah kita dalam menyelesaikan operasi perkalian.
Salah satu metode yang sedang populer belakangan ini adalah metode garis untuk perkalian ala Jepang. Metode garis merupakan metode perkalian yang diciptakan oleh Professor Fujisawa Rikitarou (1900) dari Tokyo University. Berdasarkan artikel yang ditulis oleh Fiqhan Khoirul 'Alim, Adinda Febriana Saputri dan Adib Risqy yang berjudul "JAPANESE MULTIPLICATION METHODE (JAMED) SOLUSI PERKALIAN MASA KINI", dijelaskan bahwa Metode ini dikenal di Indonesia sebagai metode perkalian Cross-Line, yaitu suatu metode perkalian berbasis geometri dengan dua garis bantu vertikal dan horizontal. Metode ini telah booming dan membuat perkalian menjadi lebih mudah dipahami dan diterapkan.
metode garis adalah metode yang dapat digunakan untuk mempermudah siswa dalam menghitung. Metode garis ini membantu siswa dalam melakukan operasi perkalian dengan cara yang lebih sistematis dan terstruktur. Metode ini sangat berguna dalam meningkatkan pemahaman siswa tentang perkalian dan mempercepat kecepatan dan ketepatan dalam menghitung. Berdasarkan artikel yang ditulis oleh Riana Dewie dengan judul "Yuk Belajar Perkalian Metode Garis", beliau mengatakan bahwa metode perhitungan ini dapat mengembangkan otak secara seimbang karena lebih mengedepankan 'pemahaman' daripada 'menghafal'. Nah, Bagi guru-guru yang masih kebingungan mengajarkan matematika untuk siswa-siswa di sekolah, metode ini patut dicoba. Silahkan coba dari angka kecil terlebih dahulu.
Metode garis memiliki keuntungan yang membuatnya menjadi pilihan yang baik dalam menghitung perkalian. Keuntungan dari metode garis adalah kemampuannya untuk menghemat waktu, karena siswa dapat dengan cepat menghitung perkalian menggunakan metode ini. Kita dapat menyelesaikan soal perkalian hanya dengan menggambar beberapa garis dan menghitung titik potongnya. Terdengar mudah bukan, sobat maths?, dengan menggunakan metode garis, siswa dapat mengembangkan kemampuan kritis berpikir, pemecahan masalah, dan ketepatan dalam menghitung perkalian.
Selain meningkatkan pemahaman, metode perkalian garis juga dapat meningkatkan akurasi dan efisiensi dalam perhitungan. Dengan memberikan pendekatan perkalian yang jelas dan terstruktur, siswa dapat menghindari kesalahan umum dan kesalahan perhitungan yang dapat terjadi pada metode yang lebih abstrak. Hal ini khususnya bermanfaat bagi siswa yang kesulitan menghafal. Metode garis juga dapat digunakan untuk menghitung perkalian dengan bilangan lebih besar dari dua, menjadikannya alat yang serbaguna dan praktis bagi siswa di semua tingkatan. Dengan meningkatkan akurasi dan efisiensi, metode garis dapat membantu siswa membangun kepercayaan diri terhadap kemampuan matematikanya dan mengembangkan sikap positif terhadap pembelajaran.
Ayo Praktik bersama!
Siapkan kertas dan pulpen yah! Mari kita ambil contoh mudah perkalian .
Ingat sobat maths! untuk angka 21, angka 2 sebagai puluhan dan angka 1 sebagai satuan, dan untuk angka 3 lainnya sebagai satuan. Lalu, kita buat garis vertikal untuk angka 21 terlebih dahulu. Kita buat dua garis sebelah kiri untuk mewakili angka 2, dan satu garis sebelah kanan untuk mewakili angka 1. Seperti ini!
Selanjutnya, kita buat tiga garis secara horizontal untuk mewakili angka 3. Seperti ini!
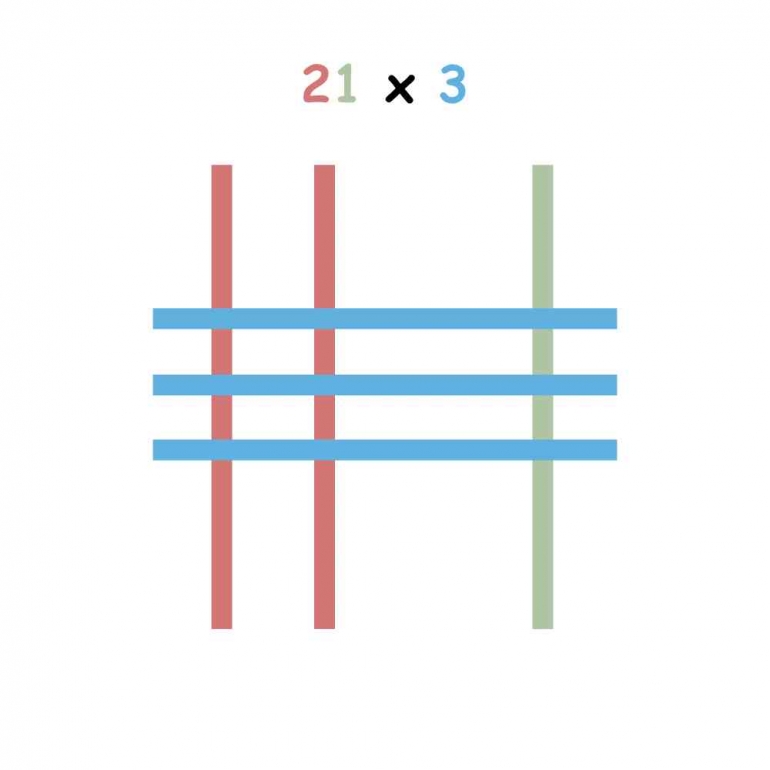
Setelah itu, kita hitung titik-titik di sebelah kiri dan kanan yang terbentuk dari perpotongan garis tersebut. Seperti ini!

Dari gambar di atas, kita dapat menghitung jumlah titik disebelah kanan sebanyak 6 dan jumlah titik disebelah kiri sebanyak 3. Maka, hasil dari 21 x 3 = 63. Mudah bukan!
Lalu, bagaimana dengan perkalian dua digit angka? Begini caranya!
Mari kita ambil contoh perkalian 12 x 23.
Sama seperti sebelumnya, kita buat garis vertikal untuk angka 12 terlebih dahulu. Kita buat satu garis sebelah kiri untuk mewakili angka 1, dan dua garis sebelah kanan untuk mewakili angka 2. Seperti ini!

Nah, untuk dua angka selanjutnya yaitu angka 23 kita buat garis horizontal. Kita buat dua garis diatas untuk mewakili angka 2, dan tiga garis dibawah untuk mewakili angka 3. Seperti ini!

Setelah itu, kita hitung titik-titik yang terbentuk dari perpotongan garis tersebut. Namun, disini ada perbedaan, kita menghitung titik dengan membagi menjadi 3 bagian. Seprti ini!

Dari gambar di atas, kita dapat menghitung jumlah titik untuk ratusan disebelah kiri atas sebanyak 2, jumlah titik untuk puluhan dengan penjumlahan diagonal sebanyak 7, dan jumlah titik untuk satuan di sebelah kanan bawah sebanyak 6. Maka, hasil dari 12 x 23 = 276. Mudah bukan!
Secara keseluruhan, metode perkalian garis dapat memberikan berbagai manfaat bagi siswa, termasuk peningkatan pemahaman, peningkatan akurasi, dan efisiensi yang lebih besar. Disisi lain, metode garis ini juga memiliki kelemahan pastinya, jika menghitung dengan bilangan yang lebih besar akan membutuhkan waktu lebih lama. Namun, dibalik kelemahan tersebut metode garis ini tetap efektif digunakan oleh siswa di sekolah loh sobat maths!. Dengan menggunakan representasi visual, siswa dapat lebih memahami konsep perkalian dan mengembangkan pemahaman yang lebih mendalam tentang bagaimana bilangan digabungkan untuk menghasilkan suatu hasil. Dengan memasukkan metode garis ke dalam pembelajaran perkalian, sobat maths dan gurua dapat memberikan alat yang praktis dan efektif bagi siswa untuk meningkatkan kemampuan matematikanya dan membangun landasan yang kuat untuk pembelajaran di masa depan.
Firlinda Fadhilah Priyantini
Sumber Referensi : https://www.rianadewie.com/2015/08/yuk-belajar-perkalian-metode-garis.html
Baca konten-konten menarik Kompasiana langsung dari smartphone kamu. Follow channel WhatsApp Kompasiana sekarang di sini: https://whatsapp.com/channel/0029VaYjYaL4Spk7WflFYJ2H












