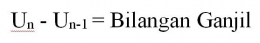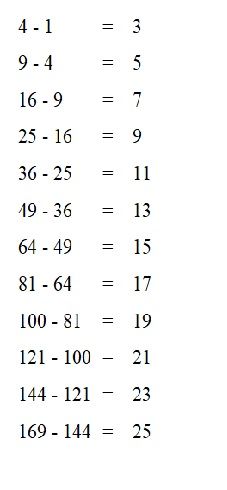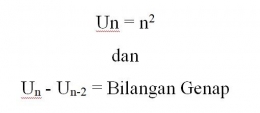"Matematika itu menyenangkan"
Ketika saya mengatakan kalimat diatas, banyak orang yang kesal. Karena menurut mereka matematika adalah mata pelajaran paling susah dan bikin pusing tujuh keliling. Masih teringat kata-kata yang sering mereka ucapkan, kurang lebih seperti ini :
"Apane seng menyenangkan, menyengsarakan dan bikin pusing onok e"
Menurut saya, dasar dari mempelajari matematika adalah rasa senang dalam mempelajari nya (sebenarnya tidak hanya matematika saja, tapi semua disiplin ilmu juga). Ketika rasa senang telah ditanamkan, pasti nya lebih mudah kita mempelajari dan memahami matematika.
Saat ini pun telah banyak media untuk mempelajari matematika, seperti buku, tulisan, dan video yang bisa dijumpai saat kita berselancar menggunakan internet. Jadi tidak ada alasan lagi, tidak suka matematika karena guru nya galak atau materi yang disampaikan kurang jelas.
Dalam kesempatan kali ini saya ingin membuat sebuah tulisan terkait bilangan kuadrat. Bilangan Kuadrat adalah sebuah bilangan positif yang di dapat dari hasil perkalian suatu bilangan tertentu dengan bilangan itu sendiri sebanyak satu kali. Bilangan kuadrat selalu dilambangkan (a^2).
Saat saya mencoba mengutak-atik bilangan kuadrat, saya menemukan beberapa hal yang menarik dan mungkin bisa membantu dalam memahami bilangan kuadrat. Di antara nya adalah, sebagai berikut :

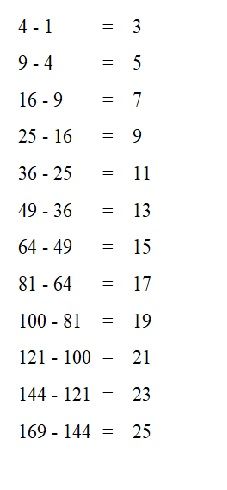

Contohnya ketika kita mengkuadrat kan bilangan yang berakhiran 1 dan 9 / satuannya 1 dan 9 maka hasil kuadratnya pasti akan memiliki nilai satuan satu ( 1, 121, 441, 961, dst) (81, 361, 841, 1521, dst). ketika mengkuadratkatkan bilangan dengan nilai satuan 2 dan 8 maka hasil kuadrat nya pasti akan memiliki nilai satuan empat (4, 144, 484, 1024, dst) (64, 324, 784, 1444, dst).
Ketika mengkuadratkan bilangan dengan nilai satuan 3 dan 7 maka hasil kuadrat nya akan memiliki nilai satuan sembilan (9, 169, 529, 1089, dst) (49, 289, 729, 1369). ketika mengkuadratkan bilangan dengan nilai satuan 4 dan 6 maka hasil kuadratnya akan memiliki nilai satuan 6 (16, 196, 576, 1156, dst) (36, 256, 676, 1296, dst). dan terakhir ketika mengkuadratkan bilangan dengan nilai satuan 5 maka hasil kuadrat nya akan memiliki nilai satuan 5 (25, 225, 625, 1225, dst).
Jadi, kesimpulannya ketika bilangan yang dijumlahkan menghasilkan bilangan 10 maka akan memiliki hasil yang serupa. 1 + 9 = 10 nilai satuan hasil kuadratnya selalu 1. 2 + 8 = 10 nilai satuan hasil kuadratnya selalu 4. 3 + 7 = 10 nilai satuan hasil kuadratnya selalu 9. 4 + 6 = 10 nilai satuan hasil kuadrat nya selalu 6. 5 + 5 = 10 nilai satuan hasil kuadratnya selalu 5.
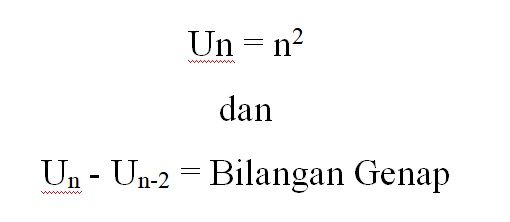
Ditemukan bahwa melakukan operasi pengurangan U3 - U1 atau 9 - 1 hasil nya adalah 8, dari hal tersebut ditemukan fakta bahwa Un - Un-2 akan menghasilkan bilangan genap (dengan syarat dimulai dari U3).
Dari fakta tersebut akan ditemukan fakta baru bahwa pengurangan dua bilangan ganjil akan menghasilkan bilangan genap dan pengurangan dua bilangan genap akan menghasilkan bilangan genap juga.
Contoh nya : U5 - U3 = 25 - 9 = 16 dan U8 - U6 = 64 - 36 = 36.
Sekian tulisan singkat dari saya terkait bilangan kuadrat. Semoga bermanfaat
Sumber:
rumusrumus.com
Umi Salamah, S.Si., M.Kom. 2018. Berlogika dengan Matematika 2 untuk Kelas VIII SMP dan MTs. Solo: Tiga Serangkai Pustaka Mandiri.
Ira Dwi Anita. LKS Matematika 2A untuk Kelas VIII SMP dan MTs. Fitur.
Baca konten-konten menarik Kompasiana langsung dari smartphone kamu. Follow channel WhatsApp Kompasiana sekarang di sini: https://whatsapp.com/channel/0029VaYjYaL4Spk7WflFYJ2H